13.7. Mysterious fountain#
| Author: | Peter Dekkers |
| Time: | 10-15 minutes |
| Age group: | 12+ |
| Concepts: | Siphon, gravitational energy, conservation of energy |
Introduction#
In this ‘black box’ demonstration, the ‘tap’ starts to flow once you pour some liquid into the funnel. It then continues to flow unassisted for a long time. What is going on? The challenge is: use your imagination and together think of a description of what might be hidden inside. Students practice developing, comparing, and testing explanations for phenomena and reflect on the role of creativity and personal input in scientific research.
Equipment#
Two bottles or Erlenmeyer flasks, one filled with water
(Optional) food coloring, two colors
Two tightly fitting rubber stoppers, each with two holes that the glass tubes fit exactly
Two large paper tubes, large enough to completely cover the bottles
A small funnel
Glass or rubber tubes
A cup with some extra liquid
The delicate tube that acts as the ‘tap’ can also be made of rubber. Use a transparent hose to connect the two bottles. Preferably use water of different colors in the cup and the container on the right to contribute to the mystery.
Fig. 13.14 The mysterious fountain.#
Preparation#
Construct the setup according to Figure 13.15. Place the bottles in the large paper tubes, which cover the bottles up to the stoppers, so that the contents of the bottles remain invisible. Note: both bottles and all tubes must be sealed airtight by the stoppers, the connection between the bottles as well. The connecting tube should protrude into these bottles as little as possible. The end of the tube below the funnel as well as that of the tube on the right in Figure 13.15 should be placed as deep as possible, close to the bottom of each bottle. The ‘tap’ should extend as little as possible above the bottle on the right, the funnel should extend as much as possible above the one on the left.
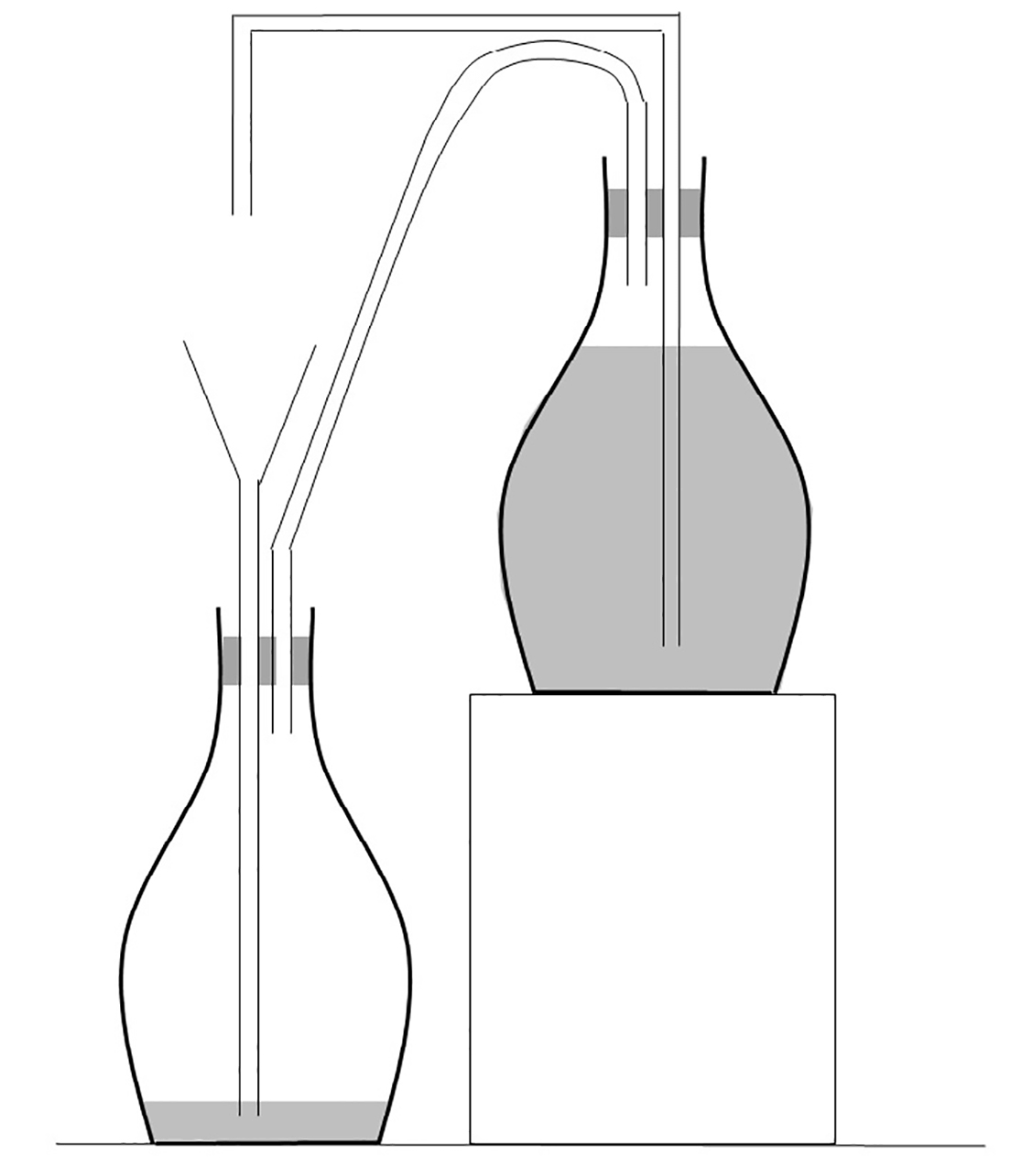
Fig. 13.15 Sketch of the setup#
Procedure#
Pour the liquid from the cup into the funnel. Then, liquid will rise in the tap tube on the right: as soon as it ‘rounds the corner,’ the tap starts to run and keeps running (as long as the liquid flows into the funnel and the liquid level in the container on the left is high enough). Yet, ‘nothing’ (visible) goes through the connecting hose between the bottles.
The discussion during the experiment is more interesting than the execution and the events. Some questions to ask and tasks to be performed (see a possible ‘scenario’ in the worksheet):
How do you think it works? (Add a sketch to your explanation, compare with your neighbor.)
Will the tap keep on running forever? Why or why not?
Nothing seems to be happening in the connecting tube. Will it still work if we remove it?
What do you think will happen if… (see the worksheet for possibilities) If food coloring is used the experiment becomes more visible and more interesting. Could the explanation involve chemical processes?
Physics background#
Lower grades#
Use Figure 13.15, when you pour a little water into the funnel, the level in the bottle on the left rises. Air is pushed through the hose into the bottle on the right. The water level there is pushed down so that water comes up inside the ‘tap’ tube on the right. The tube of the ‘tap’ is narrow, and soon the water rounds the bend and falls into the funnel. After that, the water flowing from the tap ensures that the process continues. The water stops running when the difference in water level (from the top of the water column in a tube to the liquid level in its bottle) is the same in both bottles, or when the bottle on the right is empty.
More precisely#
Once the column of liquid below the funnel is built up, and the flow is stable, the gas pressure above the liquids inside both bottles is the same. The gas pressure above the liquid in the funnel is also always equal to the atmospheric pressure prevailing at the end of the tap. Thus, the water continues to flow from the tap as long as the liquid column on the left is taller than the one on the right. According to Bernoulli, the potential energy of the excess water in the column on the left is then converted into the kinetic energy of the water flowing from the tap. It is a siphon effect: the water keeps flowing until there is no more excess potential energy available, either when the bottle on the right is empty or the liquid columns are of equal height.
Follow-up#
Lederman and Abd-El-Khalick [1998] describe how various characteristics of scientific research can be clarified to students based on their own experiences.
Tip
If it does not ‘work,’ check if the stoppers are securely fastened and the long tubes reach the liquid level in both bottles. Afterward, you can pull out the stoppers from the bottles, refill one, and start over. Be careful of overflow as some liquid has been added.
References#
- LAEK98
Norman Lederman and Fouad Abd-El-Khalick. Avoiding de-natured science: activities that promote understandings of the nature of science. In The nature of science in science education: Rationales and strategies, pages 83–126. Springer, 1998.
Worksheet
Overview
This section presents a scenario, or possible way of conducting the demonstration with examples of teacher questions, comments, and explanations aimed at stimulating the exchange of ideas and insights among students, focusing on explaining observations in scientific inquiry.
Discussion
Teacher: “I have a cup here with a strange liquid. There’s a setup here, and I’m going to pour a bit of this liquid into this funnel. What do you think will happen?”
Allow students to respond.
Teacher: “Shall we give it a try?”
Pour liquid into the funnel until the tap starts to flow.
Teacher: “As you can see, the tap begins to flow. What’s going on here?”
Teacher: “Do you think it will stop if I hold my finger against the end? And if I let go, does it start again or not?”
(The tap stops when you hold it closed with your finger but starts again when you let go.)
Teacher: “And if I catch the liquid? Do you think it will start again if I pour the liquid back in?”
(When you catch the liquid, the tap stops. Pour the caught liquid back into the funnel, and the tap starts again unless the bottle is empty.)
Teacher: “Does it make a difference if I hold one bottle lower or the other higher?”
(The height difference between the bottles does not affect the flow. The difference in liquid levels on the left must be greater than the difference on the right; the greater this difference, the faster the water flows from the tap. The bottle on the right must be placed higher than the one on the left only to allow for the tap to feed the funnel.)
Teacher: “Will this tap run forever? When does it stop, where does all that liquid come from, and where does it go?”
(The flow stops when the right bottle is empty, or the difference in height difference is zero.)
Teacher: “What’s the purpose of that connecting tube? It looks like nothing is going through. Does it still work if we disconnect it?”
(No, then it stops. If you reconnect it and add some water to the funnel, it starts again.)
Teacher: “What do the colors of the liquids have to do with anything?”
(Nothing.)
Assignments
Students: (in groups) Answer the following questions and present them to each other:
What do you think is in the bottles?
Draw your answer in the figure.
Explain how it works.
Possible extension: try to make such a device at home / with your group.
Comparison of Answers
Everyone usually thinks their own solutions are the best. But can you also explain what makes them the best? If you do not consider your own solution but only those of other groups, which do you think are better? Why?
(After the bottles are ‘revealed’:)
Teacher: “Do you understand how it works now? Explain it. Which solution(s) do you now think are the best?”
Conclusions: Characteristics of Scientific Research
Does this experiment have anything to do with science and the ways scientists do research?
Most people are surprised when the tap starts running and continues for a while. It seems there is nothing that keeps the water running. In science, experiencing surprise is very important. If what happens was unexpected, something new can be learned, and that’s what scientists find very important. To learn new things, they conduct research. In this case one approach to conducting research is to try and imagine what could be inside the bottles, and could explain what was observed. That normally results in various possible solutions that can be investigated further.
Most scientists also usually think that their own solutions and those of their friends are the best, but that’s just their opinion. To find out which solution is really the best, more research is usually needed. It could be investigated whether a proposed solution really accords with what was observed. Also you might consider carefully: is that solution understandable (does it fit in with what you already know about similar situations), or is it unrealistic? You can also build a set-up in line with the solution and see if it works. Scientists have various ways to find the best solutions.
Of course, there is technically only one solution that is completely correct for this setup. You see it when the envelopes are removed.
(If as a teacher you haven’t removed the envelopes yet, you’re setting the bar very high! Show students what’s in the bottles, project the diagram if possible, and provide the necessary background information.)
Explanation
Lower Secondary
The color of the liquids has nothing to do with it; it was only meant to make things interesting. It’s just colored water. If you pour a little water into the funnel, the level in the bottle on the left rises, pushing air through the tube into the bottle on the right, which also causes the water there to rise. The tube of the ‘tap’ is narrow, so soon the water rises, goes around the bend, and falls into the funnel. Then you don’t need to pour anymore, the water coming from the tap keeps the process going, usually until the right bottle is empty. The water stops running when the level difference in the bottles is the same, or the right bottle is empty.
Upper Secondary
A more precise explanation (beyond the level of the Dutch secondary examination program) starts with some approximations: the liquid is incompressible, the flow is frictionless, and the temperature is constant. Then consider a small section of the liquid. Its energy can change in three ways:
If the speed changes, the kinetic energy changes,
If the height changes, the potential energy changes,
If the pressure changes, work may be performed.
The law of conservation of energy can be written as: \(0 = ΔE_{kin} + ΔE_{pot} + W\)
Thus, for each volume element at every point in the circuit: \(\frac{1}{2}ρv^2 + ρgh + P = constant\)
(\(ρ\) is the density of the liquid, \(v\) is the speed at that point, \(h\) is the height, \(P\) is the pressure.)
This is Bernoulli’s law (which also plays a role in explaining how flying works when applied to a gas).
The pressure at the inflow and outflow points is atmospheric pressure. Apply Bernoulli at those points (and use also that the pressure in the air within the bottles is equal everywhere) then it turns out: the difference in height of the liquid columns on the left and right results in the speed of the outgoing liquid.