20.2. Making a slanting tower stacking blocks

Author:	Maarten van Woerkom
Time:	20 minutes
Age group:	12 and up
Concepts:	Center of mass, stable equilibrium

Fig. 20.5 A challenge: Building a slanting tower where the top block is not above the bottom block.

Introduction

If you put two blocks on top of each other, then the upper one remains stable if the center of mass is above the lower block. So the upper block cannot stick out more than ½ x the length of the block.

Would it be possible to pile up blocks such that the upper one sticks out farther?

Equipment

• A number of equal blocks.

Fig. 20.6 The demo requires only some blocks.

Procedure

Pile some blocks on top of each other with the instruction: how can you make the end of the top block stick out as much as possible? In other words, how can you achieve the maximum distance between the front of the top block and the front of the bottom block? You can use as many blocks as you want. Is it possible that the back of the top block passes the front of the bottom block?

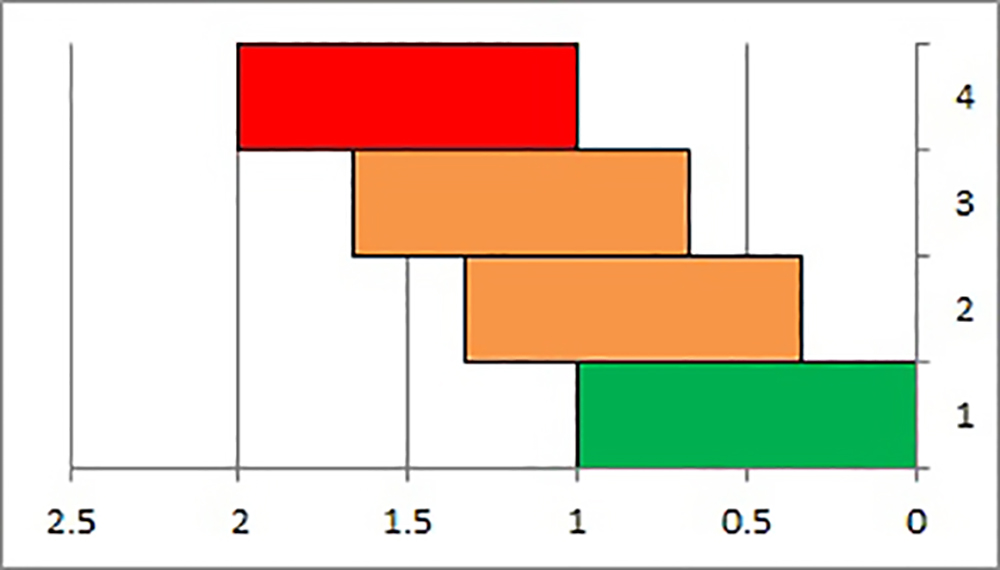
Fig. 20.7 We can try to use the approach that first comes into mind… but probably won’t succeed.

Usually blocks are stacked one by one. See the 4 blocks in Figure 20.7. First the green block (1), then the orange block (2) that sticks out 1/3 of the block length, then another orange block (3) that also sticks out 1/3 of the block length.

The center of mass of the orange blocks together is now exactly above the left side of the green block at the bottom. So if you would place another block sticking out, the red one, the pile would tip over…

It is also possible to arrange the pile in reversed order: from top to bottom (Figure 20.8). Put block one on top of block 2 (counting from above), then blocks 1 and 2 on top of block 3, etc.

Fig. 20.8 Building the pile in reversed order requires to find the center of mass each time.

Physics background

When you use the reverse piling method, starting from the top, then very quickly you reach a point where the overhang is greater than the block length.

• Center of mass of block 1 is above the front of block 2;

• Center of mass of block 1 and block 2 together is above the front of block 3;

• Center of mass of blocks 1 – 3 is above the front of block 4. All of that above block 5 and the overhang is already more than one block length.

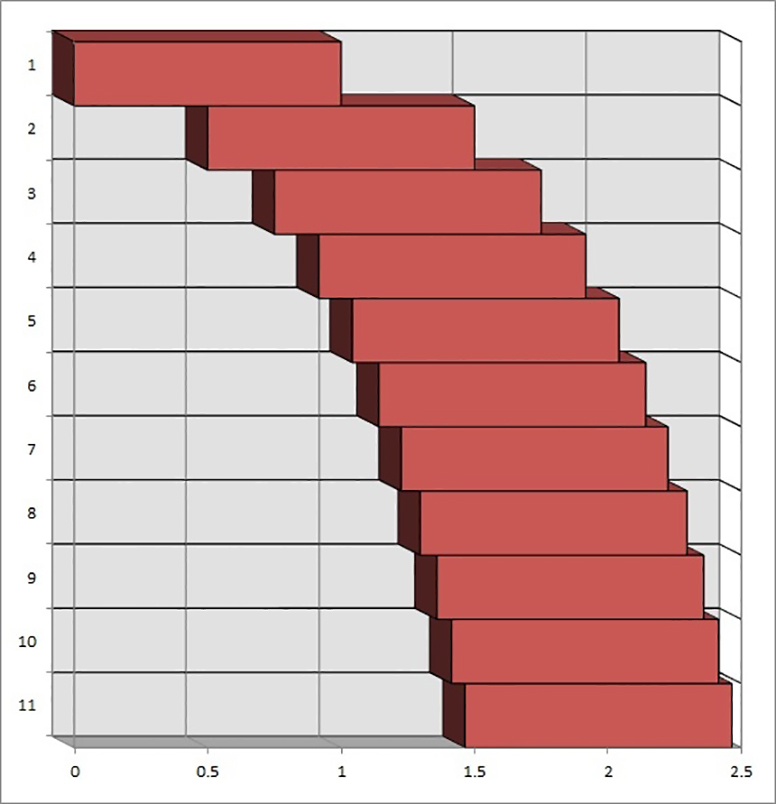
Fig. 20.9 The physics (and mathematics) behind stacking blocks

Tip

• Instead of blocks of wood you can also use CD cases or big Lego blocks.

• If you google with the term “markthal Rotterdam”, then you will see on the photographs that the 228 apartments were stacked in a way you will now understand. Teacher Eline Bijker actually started her demonstration of stacking blocks with a photograph of the market hall in Rotterdam (Figure 20.9) and asked her students which construction principle was used. The Rotterdam “markthal” is an indoor market with apartments stacked into an arch shape overhead. It was opened in 2014.

Fig. 20.10 The market hall in Rotterdam is stacked according to the principle above. Figure obtained from: https://commons.wikimedia.org/wiki/File:Markthal-Rotterdam.jpg (CC BY-SA)