18.9. Cooling metal spheres#
| Author: | Norbert van Veen |
| Time: | 20-30 minutes |
| Age group: | 15 - 18 |
| Concepts: | Cooling, specific heat, FLIR, IR |
Introduction#
To let students experience the process of cooling solid objects, we observe the cooling of iron spheres with different diameters using a FLIR camera (C5). It is clearly visible that the smallest sphere cools down faster than the larger spheres. The approach was used in an experiment conducted in the 18\(^{th}\) century by George-Louis Leclerc with the objective of determining the age of the Earth.

Fig. 18.20 The setup with a plastic test tube rack to place the spheres on.#
Equipment#
Setup with tripod and clamp or a camera tripod
IR camera
Non-conductive construction to place the metal spheres on (plastic test tube rack)
Several metal spheres (of the same material) differing in diameter
Kettle
Ladle
Tea towel.
This description uses Coach 7 as measurement software. The measurement file using this software is.
Preparation#

Fig. 18.21 Another view of the setup looking at the test tube rack to place the balls on and an IR camera filming.#
Set the IR camera to the correct IR distance and visual distance. Set up a measurement with a measuring spot or, if desired, a measurement with a ‘hottest spot rectangle’ (drag it to the desired size on the touchscreen). Set the emissivity to around 0.95 (for iron), look up the value of this emissivity for other metals if spheres of other materials are used.
When using Coach 7, set up ‘measurement with synchronized display’. You can also film the setup with any camera app on your device, then select the FLIR C5 as the camera.
Procedure#
Show the spheres to the students and provide them with the diameters of the spheres. Let them calculate the mass using the material density.
Let the students calculate how much thermal energy a sphere possesses when it heats up from room temperature to a certain temperature (for example, 60°C). Dutch students can find the specific heat of the material in BINAS.
Ask and discuss briefly: Are the temperatures of the spheres at the start of the experiment the same or different?
Ask and discuss: Of the following options, what do you expect will happen?
The largest sphere will cool down the fastest.
The smallest sphere will cool down the fastest.
Cooling will occur at the same rate for both spheres. Preferably, have them write down their choice and come up with an explanation.
Boil some water in the kettle, leave the lid of the kettle open and place the spheres in a ladle in the kettle. Wait a moment until the metal spheres are heated up. Remove the ladle from the kettle and place the spheres on a tea towel to quickly dry them. Then place the spheres in the desired position in your measurement setup.
Perform the measurement. After heating the spheres in boiling water, quickly position them in the setup. Start the measurement with the FLIR IR camera.
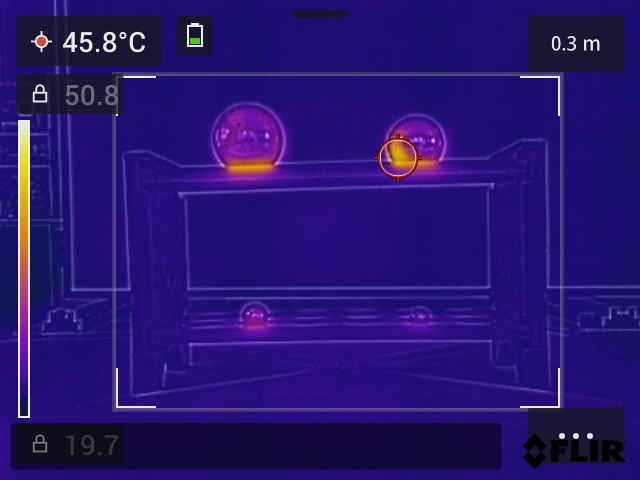
Fig. 18.22 Screenshot of the FLIR C5 measurement. The temperature range is set manually.#
Discuss the results. Which explanation fits best?
Optionally tell the tale of George-Louis Leclerc and his determination of the age of the Earth.
A question to check students’ understanding: Can you determine the age of the Earth with this method?
Tip
Project the measurement via the computer onto a screen or interactive whiteboard. Ensure that the temperature is easy to follow, for example by aiming a temperature spot from the camera at a sphere. The FLIR C5 camera can also be set to a manual temperature range, so that the room temperature is not visible (see Figure 18.22).
Place the spheres on a surface such as chocolate bars, so that the amount of thermal energy per sphere is visible afterwards by the amount of melted chocolate.
Place the spheres in an oven to reach a higher temperature. Be extra careful when handling the spheres then.
Physics background#
A smaller sphere has a relatively larger ratio of surface area to volume, allowing the sphere to more quickly release energy to the surroundings (\(\frac{A}{V} = \frac{3}{r}\) for a sphere). A smaller radius will result in faster energy loss to the surroundings. For more detailed explanation, see the note below.
Note
In this experiment, we look at the heat exchange of metal (iron) spheres that differ only in diameter. Objects contain thermal energy. If an object has a higher temperature than the ambient temperature, it possesses more thermal energy. When the object cools down, it will lose this thermal energy through, in this case, IR radiation. The spheres release energy to the environment according to:
\(\frac{dQ}{dt} = P = -k \cdot A \cdot (T - T_{\text{env}})\)
The spheres have an energy given by:
\( Q = m \cdot c \cdot \Delta T \)
which leads to:
\( \frac{dQ}{dt} = m \cdot c \cdot \frac{\Delta T}{dt} \)
Thus, the energy balance for a cooling sphere is:
\( m \cdot c \cdot \frac{dT}{dt} = -k \cdot A \cdot (T - T_{\text{env}}) \)
After integrating, this gives:
\( \frac{T - T_{\text{env}}}{T_{\text{begin}} - T_{\text{env}}} = e^{-\left( \frac{k \cdot A}{m \cdot c} \right) t} \)
The term in the exponent determines the cooling rate. Therefore, to compare the spheres, we need to compare this term for the different spheres. Let a large sphere have radius \(R\) and a small sphere have radius \(r\).
For the small sphere:
\( \frac{kA}{mc} = \frac{kA}{\rho \cdot V \cdot c} = \frac{k \cdot 4\pi r^2}{\rho \cdot \left( \frac{4}{3} \pi r^3 \right) \cdot c} = \frac{k}{\rho \cdot c} \cdot \frac{3}{r} \)
For the large sphere, we find:
\( \frac{k}{\rho \cdot c} \cdot \frac{3}{R} \)
The ratio of the energy loss rates is then:
\( \frac{\text{small}}{\text{large}} = \frac{\frac{k}{\rho \cdot c} \cdot \frac{3}{r}}{\frac{k}{\rho \cdot c} \cdot \frac{3}{R}} = \frac{R}{r} \)
Since \( \frac{R}{r} \) is greater than 1, the energy loss of the small sphere is faster.
Follow-up#
Use a temperature sensor attached to a large and a slightly smaller sphere, perform the measurement using appropriate software. Ask questions like:
How meaningful is the measurement this way?
How quickly do they both cool down?
What influence does the temperature sensor itself have?
The sensor also needs to heat up, in the case of a too small sphere, this will cost a lot of thermal energy from the sphere and therefore it will cool down even faster.
