10. Argumentation#
10.1. Development of inquiry skills through demonstrations#
Conducting scientific research is a matter of making targeted and careful observations and applying your knowledge to understand them, and vice versa, of adjusting your knowledge and determining with which subsequent observations you can test and substantiate claims. Demonstrations are an excellent opportunity to practice this with students. Examples of the many important questions that need to be addressed during inquiry are:
What can I conclude from these observations?
How confident am I about this, can the conclusion be strengthened?
If I change something, what will happen?
And if the outcome changes or not, what will I learn from that?
This thinking-back-and-forth between practice and theory characterizes research [van den Berg, 2013]. In demonstrations, you can stimulate that thinking, guide it, and help improve it in a pleasant, motivating and safe way. As always, the art here is in maintaining the balance between challenging students, providing them with the autonomy to think and do for themselves on the one hand, and supporting, scaffolding, encouraging and guiding their thought and action on the other. Allow students to choose and do by themselves where they are already capable. But as a teacher, provide examples and support with what is still too difficult. Select the learning objectives for your demonstration from the range where students show cognitive readiness. Limit the number of objectives, and peg them at a level that they can achieve with some effort. Provide your students with a route using guiding questions and assignments, but also with challenges and opportunities for their own input and personal contributions.
Fig. 10.1 The signing rod, how many measurements do we need before we have a ‘convincing’ value for Young’s modulus for a specific material?#
Learning physics requires doing physics. But is that possible by participating in demonstrations? After all, demonstrations do not serve to actually solve scientific problems, nor do students manipulate the materials by themselves… They should suggest to students that with a little effort they too can eventually understand the surprising phenomena - a guarantee that is not provided in real physics research. As a teacher you know the outcome and conclusion in advance, all you have to do (difficult as that may be) is to produce the intended observations. It suffices to then present the accepted corresponding explanation, basically confirming what scientists already know. While this is a viable approach, it need not stop there. In your demonstration you may use the opportunity to contribute to the development of inquiry skills, which is not difficult at all.
To that end, make the research problems manageable before confronting your students with them. Reenact the solving of those problems, as it were, during your demonstration, because there is a lot to learn from that. The easiest way to do this is to ask your students questions like:
What do you think will happen?
What do you know about the set up?
What exactly did you see? What did you notice?
How would you describe your observations as accurately as possible?
Was what happened what you expected to happen?
If we would repeat the demonstration, what would you pay special attention to?
How can we improve our observations?
Can you explain what happened and why it happened?
Did we learn something from what was observed? How does that fit with what we already know? What remains unknown so far and how can we find out?
By finding the answers together, valuing them, testing them where possible, students practice the skills they need when they “learn physics” and “do physics” on their own later on. The demonstrations in Part Demos on scientific inquiry of this book focus explicitly on these skills, but in principle all the other demonstrations are suitable as well. Of course, you will have to adapt them to your own needs and include your own ideas. Furthermore, you would not ask all of the questions suggested above in a single demo as that would be far too strenuous for both students and teacher. Choose a clear, well-defined learning goal and give it some extra attention using a few appropriate questions. Examples follow below.
Fig. 10.2 By finding the answers together, valuing them, testing them where possible, students practice inquiry skills. Figure created with AI.#
We distinguish three levels of difficulty that depend on what learning we aim for. In the simplest demonstration, a surprising phenomenon is shown and your students practice scientifically “observing” and “interpreting”. At the second level, observations are not merely interpreted explicitly, a conclusion is drawn as well and substantiated through arguments based on the observations. The third level demonstration involves skills that address the limits of the knowledge found. Guiding questions are, for example, What assumptions have been made?’ Or: ‘In what situation is the conclusion no longer valid?” Part of exploring these limits is also a consideration of knowledge-extension beyond those limits. Can the conclusion be generalized? Does the conclusion raise new questions, and how can they be answered?
In inquiry beyond these three levels students need all their investigative skills combined. As a teacher, you may realize that you no longer have all answers available. After all, at this most beautiful but most difficult level, students engage in real physics research.
10.2. Argumentation#
In scientific research, merely finding an answer to the research question does not suffice, as only the most scientifically convincing answer is satisfactory. In the classroom setting, then, you are faced with at least two different challenges. First, how do you get students to strive for finding the most convincing answer? And second, how do you teach what counts as convincing in the natural sciences, and more specifically in physics?
‘Argumentation’ is understood here to be the production and critical evaluation of an optimally convincing answer to a scientific research question. Many demonstrations focus on showing connections with practice and visualizing concepts. Many other practicals focus on enabling students to do inquiry and contribute to developing investigative skills to produce convincing data. However, demonstrations can also be focused - if you frame them a little differently - on understanding why the data are convincing. On understanding of the nature of evidence and the need to convince yourself and others that the explanation you have found for your observations is the best explanation possible.
Example: the most convincing conclusion#
With Grade 10 students, the class jointly measured on one setup to determine the relationship between the length and resistance of a constantan wire. Students were asked to use the values found (wire lengths l and the determined resistance) to write down a conclusion about the relationship between length l and resistance R of the wire. Some typical answers (after weeding out unusable ones) are listed below, numbered 1 to 4. The teacher collected and ordered them from weak to stronger before discussing them with the class. First the weakest:
As the length changes, so does the resistance.
Students were asked if they thought this is a proper conclusion, why or why not, and if they could think of an even better conclusion. When thinking about the quality of the conclusion, a context may help. For example: suppose that the wire is part of the circuit in a device that explodes if too much current flows. The research task: determine the length of wire needed for a maximum but safe current of \(X\) amperes.
The context serves to make the quality of the conclusion tangible and important, as it should help to create a safe device that works well.
Next, previous student answers were presented one after the other, statements 2-4, in order of increasing quality. Each time students were asked to think of an even better conclusion than the one presented.
As the length increases, so does the resistance.
If the length increases twice as much, the resistance also increases twice as much.
The resistance is directly proportional to the length where \(R = 14.5·l\).
The class concluded that you can’t do much with answers 1-3, doing research with results such as these is pointless. They noted also that answer 4 becomes even more convincing by presenting the corresponding evidence (e.g., a graph).
Students in Grade 10 can usually identify the fourth answer as the best. But what makes it the best? What are the characteristics of the best answer? What makes an answer helpful in determining exactly how long the wire should be in the fictional device? Once they have answers to those questions and know that these are what is worth remembering from this activity, its goal has been attained. With a little coaching, students should be able to figure out that an answer is better if it:
contains more information (‘increase’ is more informative than ‘change’)
gives more detail (‘twice as large’ is more detailed than ‘increase’)
contains numbers in addition to words (only when you know the ratio can you calculate the length).
A nice final conclusion to this activity could be: the answer to the research question should be consistent with the measurements and be as informative, complete and useful as possible. The concepts of ‘informative, complete and useful’ should have become more concrete and clear. They should provide a practical stepping stone towards developing the overarching, but abstract concepts of validity and reliability (of measurement results, interpretations and conclusions) [Pols et al., 2022].
10.3. ‘Rebuilding a demonstration’#
Argumentation is important not only in drawing conclusions; it plays a central role in every phase of an investigation [Pols et al., 2022]. Below, some examples illustrate how the demonstrations on this site can easily be adapted for “learning to do argumentation” in other phases of research. We show this first based on the demonstration Up and down the hill from this collection and then with another demonstration. These practical examples can later be used at one’s discretion to convert other demonstrations.
Fig. 10.3 In the (\(v,t\))-diagram, the direction coefficient of upward motion is different from that of downward motion.#
Demonstration Up and down the hill focuses on the idea that the acceleration of an up-and-down movement at the highest point is not necessarily 0. So the focus is on developing conceptual knowledge. How can we focus this same demonstration on argumentation?
If you look closely at the (\(v,t\))-diagram in Figure 10.3, you can see that the inclination of the graph is not constant. When the trolley rolls upward, the acceleration seems to be greater than when it rolls downward. Is that a measurement error? Is the friction different? Is there some physical phenomenon that provides a possible explanation? After the students suggest some possibilities the question becomes, what can we do to investigate this? For example, one could turn the cart around and see if the graph remains the same. Should we perhaps look at other quantities than the acceleration to get a better view of what exactly is happening? Suppose someone suggests that the direction of the frictional force reverses at the top and could cause a kink in the (\(v,t\))-graph. How could they convince others of this? For example, what graph could they use to argue the point?
In a demonstration, identify the different goals and then select one goal to focus on. Keep it manageable for your students and yourself, focus on one or two aspects of argumentation, and expand to other aspects next time, gradually expanding the issue. You don’t have to cover everything in a real investigation all at once.
Example: The swinging pirate#
After Pols et al. [2022], students first watch an exciting clip from a pirate movie in which the hero swings from one ship to another on a long rope, while swords flash and explosions go off everywhere. The assignment: design a new stunt for such a movie, in which the hero lands on the second ship at exactly the right moment. To do this, do research using a model: a mass piece hanging from a string. The first step in the research is an orientation to the situation and determining the research question.
Fig. 10.4 The context of a pirate swing is taken from Pols [2023].#
Orientation: What needs to be researched?
Translating the pirate’s movement to a mass piece on a string is not that difficult. Based on the context and knowledge about swings, we have seen that students can create initial research questions about the factor that can influence the “swing time” and have testable expectations in that regard. (The informal term ‘swing time’ refers to the time it takes the pirate to reach the other side. The term ‘period’ is introduced only if students express a clear need for it, which they often do not at this stage.)
Using the research questions they come up with, the same approach as was used with the conclusions about the constantan wire can be applied again. If necessary add your own ideas to the research questions they come up with, and present them in order of increasing quality. Presenting them one by one, ask whether they think it’s a good research question, how it could be made even better, and what they think is improved each time.
These are some examples of research questions for a mass piece swinging back and forth on a string, in order of increasing quality:
How fast does the mass piece swing?
Does the swing time change when the mass of the mass pice is changed?
Does the swing time increase as the mass of the mass piece increases?
Is the swing time proportional to the mass of the mass piece?
What formula or graph can you use to find the swing time if you know the mass of the mass piece?
Questions for discussion: Is this a good research question? Why or why not? Can you think of an even better one? Do the answers to questions 1-4 help the stunt person in any way? What would help?
Together, detect what are the characteristics of a good research question. Again, you can aim for a nice final conclusion: physicists in their research often try to establish a relationship (or lack thereof) between an independent and dependent variable. This is a fundamental insight. If you can’t figure out what to measure, you usually can’t even begin your research!
Controlling variables and measuring them fairly
Once a good research question is available it is time to start thinking about how to make suitable measurements. For the pendulum test, students in grade 10 usually do figure out that in addition to mass, the swing time may depend on the initial angle and length.
Before you then start measuring, you can ask students: how are we going to do this? Make that question concrete, for example as follows: I have prepared tables to fill in the readings. Which of these do you think is best, which is worst, and why?
Fig. 10.5 Tables at ‘controlling variables#
Based on the tables shown here, you can encourage students to think about the interval between measurements, the range in the independent variable(s), and the concept of fair measurement. This is meant to have them consider in advance the consequences of the choices to be made during the collection of data, and their impact on the quality of the answer that is yet to be found. This can help them to plan a step they very easily skip in independent work. After the discussion, the class can prepare its own tables for use in the demonstration, and think as a team about why these tables are satisfactory.
Another option is to deliberately (allow them to) choose an unsuitable table (e.g., Table 10.5) in your demonstration, have the students experience its awkwardness and discuss that after doing a few measurements. In this particular example this approach is less suitable if the influence of mass is investigated, since it has no systematic influence on the swing time, which would complicate the discussion. In the investigation of the influence of the length however the approach with an unsuitable table can be very instructive.
Next ask the class to draw a conclusion, and to check carefully whether that conclusion can be defended on the basis of the data. Make the meaning of ‘checking carefully’ clear and concrete, with questions such as:
Could the change also have been caused by something else?
Do you now also know what happens if you make the length ten times greater?
How sure are you of the shape of the graph between measurements?*
Most students will only put time and energy into finding and using the correct measuring methods when they see what all that effort is good for. You can tell them that, but we think it is more instructive if students think about it themselves and try to give their own reasons in an activating approach. In practicals, that can quickly become cumbersome, but in demonstrations this can be done quite smoothly and collaboratively. These ‘correct methods’ are of course not immediately available and final, but fit into a learning pathway for ‘learning to investigate’.
Interpreting measurements
The absence of an influence of mass and (small) initial angle on the period is often not explored in common practicals and demonstrations about the pendulum. A missed opportunity! Just when students expect an influence that is not there (according to theory) interpreting the data becomes a real problem that requires a solution. After all, while there will be fluctuation in measurements due to measurement errors, but do these imply that there is an influence or not? What could cause the fluctuations: the measurement method, outside influences, or a possible relationship between the quantities? Because students are often inclined to analyze and present their data in such a way that they confirm what they expected to find, making work of this can be useful. Feel free to let them help carrying out the measurements, throw in some friendly challenges: You’re getting different results every time, can’t you try to do better? Or: * we have repeated the measurement a few times, would it help to average the results?* And: you measured really well, and you see something different from what you expected. Which is more convincing, what you see or what you expected? In this ways, you work on developing argumentation skills by focusing on reasons for repeating measurements, minimizing measurement error, and reporting dispersion.
For a definitive answer to the question whether mass (or initial angle) affects the pendulum, set up two pendulums of equal length but different mass (or initial angle) and release them simultaneously. Carefully prepared they will keep swinging nicely side by side. But if you want students to learn to investigate for themselves, avoid doing this right away. Although doing so quickly confirms of the targeted conceptual relations it would completely prevent students from starting to think for themselves about inquiry. By the way, this is also an example of using the power of demonstrations in which nothing actually happens!
Representing measurements
Based on the well-known formula, it is common practice to plot the period against the square root of the length. However, this is not evident for students, so it is better to start by placing the independent variable on the horizontal axis. We also do not know the exact formula yet; we want to investigate it precisely… But suppose they suspect a relationship; what kind of activating instruction will make students think about what should be placed on the axes?
One option is to show graphs 1-4 and present the following questions to the class:
Determine which of the graphs 1-4 is incorrect and does not match the measurements.
Choose a graph yourself and determine the relationship between period \(T\) and length \(L\) from it.
If you have chosen your graph wisely in question 2, how did you make your choice?
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
L = np.array([0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6])
T = np.array([0.9, 1.3, 1.6, 1.8, 2.0, 2.2, 2.4, 2.5])
fig, axs = plt.subplots(2, 2, figsize=(10, 10))
# Plotting data on each subplot
axs[0, 0].plot(L, T,'k.')
axs[0, 0].set_title('$T$ as function of $L$')
axs[0,0].set(ylabel='T')
axs[0, 1].plot(L, T**2,'k.')
axs[0, 1].set_title('$T^2$ as function of $L$')
axs[0,1].set(ylabel='$T^2$')
axs[1, 0].plot(L, np.sqrt(T),'k.')
axs[1, 0].set_title('$\sqrt{T}$ as function of $L$')
axs[1,0].set(ylabel='$\sqrt{T}$')
axs[1, 1].plot(L, np.sin(T),'k.')
axs[1, 1].set_title('$sin(T)$ as function of $L$')
axs[1,1].set(ylabel='$sin(T)$')
# Adding common labels
for ax in axs.flat:
ax.set(xlabel='L')
# Adjust layout
plt.tight_layout()
# Display the plot
plt.show()
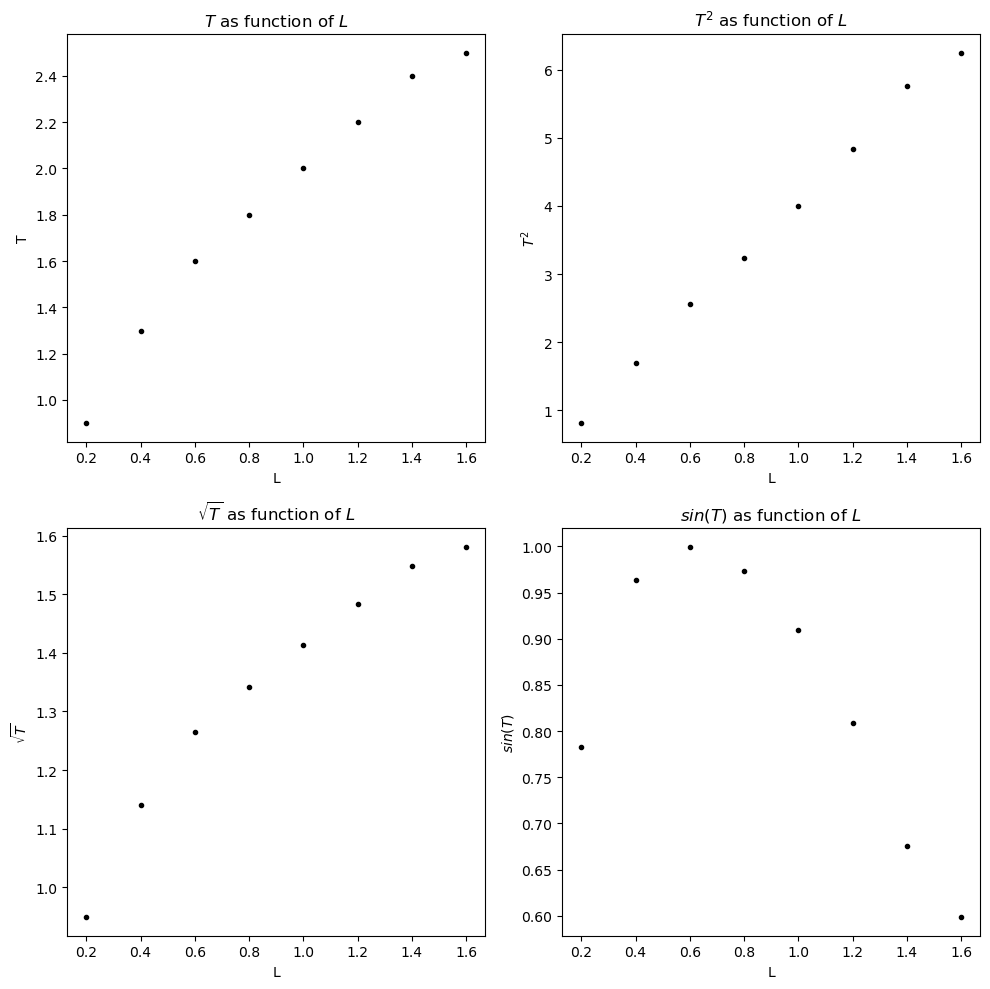
We believe that the chance of students understanding why you plot \(T^2\) against \(L\) rather than \(T\) is greater in this situation than when you prescribe what the graph should look like. They realize that they must always choose the most appropriate representation. In all these activities, it keeps coming back that you need to formulate as complete, clear, substantiated, and usable an answer to the research question as possible.
The described examples concern orientation on the problem and determining measurable quantities, choosing the range and interval between measurements, representing and interpreting measurements, and drawing conclusions. However, argumentation is equally important in formulating expectations, choosing measurement instruments and procedures, connecting practice with theory, and formulating questions for further research, to name a few. The challenge to the reader is to come up with and try out these generalizations themselves, for example in the demonstrations described in this book, but preferably also in other educational activities.
10.4. References#
- Pol23
Freek Pols. Development of a teaching-learning sequence for scientific inquiry through argumentation in secondary physics education. PhD thesis, Delft, University of Technology, 2023. doi:10.4233/uuid:df26ce2c-4b0f-41ee-93ff-301aa82457c3.
- PDDV22
Freek Pols, Peter Dekkers, and Marc De Vries. Defining and assessing understandings of evidence with the assessment rubric for physics inquiry: towards integration of argumentation and inquiry. Physical Review Physics Education Research, 18(1):010111, 2022. doi:10.1103/physrevphyseducres.18.010111.
- PDdV22(1,2)
Freek Pols, Peter Dekkers, and Marc de Vries. ‘would you dare to jump?’fostering a scientific approach to secondary physics inquiry. International Journal of Science Education, 44(9):1481–1505, 2022. doi:10.1080/09500693.2022.2083251.
- vdB13
Ed van den Berg. The pck of laboratory teaching: turning manipulation of equipment into manipulation of ideas. Scientia in educatione, 4(2):74–92, 2013.