17.13. Floating pearls#
| Author: | Peter Dekkers |
| Time: | 30 minutes |
| Level: | Grade 10 |
| Concepts: | Free fall, projectile motion, horizontal launch |

Fig. 17.24 Ticker (height 2.4 cm, frequency 100 drops/s) and parabola of drops.#
Introduction#
This demonstration beautifully shows the independence of motion in mutually perpendicular directions. In this demonstration, the example of horizontal projectile motion is used where water droplets are the projectiles. The principle is clarified almost entirely conceptually, without quadratic equations but with stunning visuals.
Equipment#
Dark room that can preferably be fully darkened
Overflow vessel (see Figure 17.25)
Two stands
Height-adjustable table
Clamps
Ticker timer
Bicycle valve tube (> 80 cm)
Faucet with (about 1.5 m) flexible tube
Sink
Stroboscope
Ruler
Warning
Stroboscopic lighting can trigger seizures in people with certain kinds of epilepsy; this demonstration is not suitable for them.
Preparation#
Place a stand on the table next to the faucet by the sink.
Attach a hose to the faucet.
Attach the overflow vessel to the stand at a considerable height, letting the hose from the faucet hang into it.
Attach one end of the valve tube to the outlet of the overflow vessel.
Attach the ticker timer with a clamp to the second, securely clamped stand, slightly lower than the vessel.
Normally, your ticker timer taps with a point on carbon paper to make dots on a paper strip. It will now tap on the valve tube to produce water droplets, but that point might puncture the tube. Therefore, remove the plate on which the point is situated, turn it over and re-attach it, with the point facing up and the tube underneath. Make sure it is loosely attached and water can still flow through the tube.
Position the ticker timer and valve tube so that a stream of water flows horizontally out of the hose and falls from a considerable height into the sink.
Finally, set up the stroboscope to illuminate the falling water stream from the side.
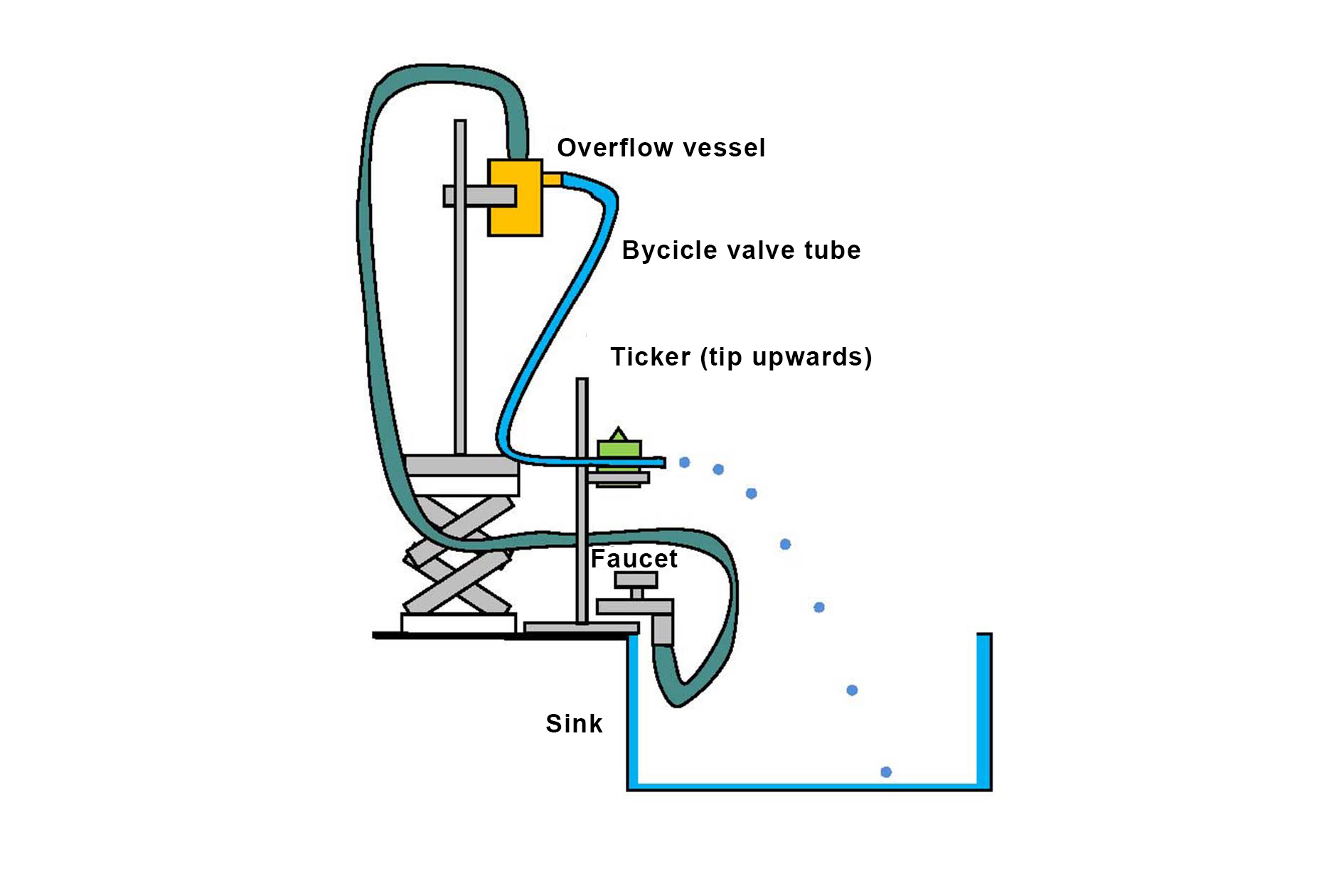
Fig. 17.25 The setup.#
Next, some fine-tuning is required:
Turn the faucet on slightly, adjust so that after a while, the outflow through the spout is exactly the same as the inflow from the faucet. The overflow vessel ensures a constant pressure on the outgoing water stream.
Adjust the positions of the vessel and the ticker timer so that the stream falls into the sink in a nice arc. During the demonstration you will want to change the height and make various arcs: ensure that for the whole intended range the water falls into the sink.
Turn on the ticker timer. Adjust the vibrating plate pressing on the valve tube so that it produces individual droplets. (You will only see the individual droplets under stroboscopic lighting but the ticker timer rattles, no longer hums, when properly adjusted.)
Darken the room, and illuminate the falling water with the stroboscope from the side. Adjust the frequency so that the droplets appear to hang motionless in the air, forming a parabola.
Adjust the flow rate by changing the height of the table with the overflow vessel.
Procedure#
Your demonstration might proceed as follows, starting from when the audience sees the droplet parabola.
“How long does a droplet take to fall from the ticker to the edge of the sink?” From the vibrating frequency, you get the time between two visible droplets (In the photos: 0.01s). That is the time it takes a droplet to move between the visible positions. Count the number of floating pearls in the arc (Figure 17.24) and you know the duration of the fall.
“The pattern seems regular. What is regular about it?” Not only the time taken but also the horizontal distance moved between successive droplets is equal (Figure 17.26). You can measure this. From this, the horizontal speed of each droplet follows. It remains nearly constant during the fall.
Fig. 17.26 Small initial speed.#
“How could we increase the horizontal speed?” If you hang the overflow vessel higher, the outflow speed increases (Figure 17.27). The arc widens and initially descends less steeply.
Fig. 17.27 Large initial speed.#
“If we hang the vessel higher, the outflow speed increases. So the arc widens. Does the fall of a droplet take longer now? How can you see that?” The number of floating pearls in the arc does not change, so the duration of the fall is the same as before. No matter how you change the height of the vessel, the duration of the fall is always the same for the same height of fall. The fall of the droplet is a combination of horizontal and vertical motion, and these two motions proceed independently.
“The vertical distance between the droplets increases. What does that mean for the vertical speed of the droplets?” The vertical distance between successive droplets grows: they accelerate in the vertical direction. Measurements of the vertical distances between the droplets roughly show: the same vertical distance is added to the falling distance of successive pairs of droplets. (The “increment” of the falling distance in successive time intervals is constant.)
“What is the name of this type of motion, in which the vertical speed increases uniformly?” This is a uniformly accelerated motion. Using ‘g’ and noting that droplets are produced at a rate of 100 Hz, the vertical distance expected between successive pairs of droplets increases by 1 mm. This is too small for live direct measurement with a ruler, but can be measured sufficiently accurately using a photo (Figure 17.27).
From the measurements, an approximate value for g can be determined. With time intervals of \(0.01\) s and noting that the distance increase is indeed \(0.001\) m in the photo, the increase in the average speed is \(\frac{0.001}{0.01} = 0.1\) m/s, and the acceleration is \(\frac{0.1}{0.01} = 10\) m/s\(^2\). During the fall, the vertical speed increases uniformly.
Tip
Always fun to finish: increase the stroboscope frequency a bit, and the droplets will climb up the parabola, ‘back into the faucet.’ Also nice: zoom in on the part where the stream breaks into individual droplets, the stroboscope beautifully shows this process. If you can’t use your own photos, you can use those from this article: the originals can be found on the website and enlarged. The scale of the photos is based on the height of the ticker: it is 2.4 cm in reality.
Physics background#
Each droplet undergoes identical horizontal projectile motion. The droplets are launched at fixed time intervals. When illuminated briefly at the end of each time interval, each droplet precisely occupies the position of its predecessor at each subsequent flash. Thus, the parabola of droplets appears to be hanging still in the air (if the stroboscope and ticker time are at the same frequency).
If illuminated at the end of slightly longer intervals (lower strobe frequency), the droplets appear to move slightly beyond where their predecessor was, and collectively they appear to move slowly downward. If illuminated at slightly shorter intervals, they appear to move upward, back toward the ticker timer. In the beginning of the stream, you don’t see individual droplets; they form later as the accelerating pieces of water are pulled apart. The ticker timer apparently creates almost evenly sized droplets with equal intervals. Cohesion does the rest.
