Speed of light in a liquid

14.9. Speed of light in a liquid#

Author:	Norbert van Veen
Time:	20-30 minutes
Age group:	15-18

Introduction#

Modern smartphones have a LiDAR sensor. This sensor allows you to measure the distance to objects. The LiDAR sensor is designed to measure only in air. As the speed of light in a transparent substance is slightly different than the speed of light in air, the measured distance is different. You can use this ‘measurement error’ to determine the speed of light in a transparent liquid.

../../_images/demo62_figure1.png — Fig. 14.17 The LiDar used in this experiment.
*left:* LiDAR sensor on the phone.
*right:* Screenshot of LiDAR app.#

Materials Needed#

Smartphone with LiDAR sensor (iPhone 12 or higher) and a LiDAR app (phyphox) or the app LiDAR pointer
Tripod
Pan
Liquid (e.g. water)
Tape measure

Preparation#

Place the phone in the tripod above the table. Ensure that the phone is perfectly horizontal. This can be checked with an app that indicates the tilt.
Place a pan directly under the phone’s LiDAR sensor (see Figure 14.17 at the right). Make sure the LiDAR sensor is aimed directly at the center of the pan.
Verify the distance from the phone to the bottom of the pan using a tape measure.

Procedure#

Provide some explanation about the operation of echo and sonar. Explain that this also works with invisible laser light, such as used in speed limit enforcement.
Explain the demonstration. Indicate that you will perform a distance measurement with a phone with and without water.
Draw a diagram on the board, such as the drawing in Figure 14.18.
Explain how the LiDAR sensor provides a distance measurement.
Explain that you will pour water into the pan and then measure the distance again.
Let the students predict what effect the water in the pan will have on the measurement.
Carefully pour the water into the pan. Ensure that the water has come to rest. Use a water height of 5-8 cm.
Perform the measurement and note the measured distance on the phone with (S4) and without water (S1). Note the height of the phone to the water surface (S2). Measure the depth of the water (S3).
Calculate the speed of light in water, assuming speed of light in air is 299702547 m/s.
The speed of light in water is determined with a single measurement. Ask students how they could obtain a more accurate value. (Students can repeat the demonstration with different water heights and use a more sophisticated way of determining the speed of light.)
The following question can be asked to assess students’ understanding: If we were to pour the same amount of another transparent liquid with a higher density into the pan instead of water, what would the LiDAR sensor indicate?
- A shorter distance than with water.
- A longer distance than with water.
- The same distance as with water.

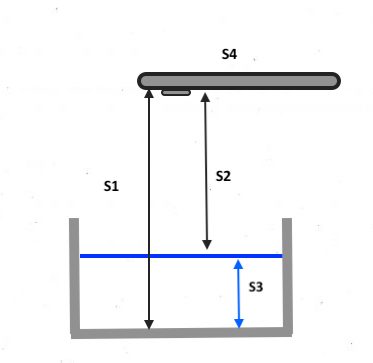
../../_images/demo62_figure2.jpg — Fig. 14.18 S1 is the actual distance between the phone and the bottom of the pan, S2 is the distance between the phone and the water surface. S3 is the water depth. S4 is the distance measured by the app.#

Physics background#

LiDAR is a technology that determines the distance to an object or surface with laser pulses and works on the same principle as radar. The LiDAR sensor determines the distance to the object or surface by measuring the time elapsed between sending a pulse and receiving a reflection of that pulse:

\[ s = \frac{c \Delta t}{2} \]

with \(s\) the distance in m, \(c\) the speed of light in m/s and \(\Delta t\) the time between sending and receiving the pulse. The laser pulses will travel more slowly in water:

\[ n_{a\rightarrow w} = \frac{c_{air}}{c_{water}} \]

This longer travel time results in an ‘erroneous’ measured distance (S4) of the distance from the LiDAR sensor to the bottom of the pan. The speed of light in water is calculated using the time that laser light stays in the water, see [Bewersdorff and Weiler, 2022]:

\[ t_{water} = t_{measured} - t_{air} \]

\[ t_{water} = \frac{S4}{c_{air}} - \frac{S2}{c_{air}} \]

\[ c_{water} = \frac{S3}{t_{water}} \]

Depending on the measurements, we find deviations from the literature value for \(c_{water}\) (\(225\cdot10^6\) m/s) between 0.5 – 10%.

../../_images/demo62_figure3.jpg — Fig. 14.19 The experimental setup#

Tip

Depending on the power of the LiDAR sensor, the water depth cannot be too great. There will be a power loss; maintain a depth between 5-8 cm.
Ensure the phone is securely fastened, as it may fall into the water.

References#

BW22: Arne Bewersdorff and David Weiler. Measuring the speed of light in liquids with a smartphone. The Physics Teacher, 60(6):516–517, 09 2022. doi:10.1119/10.0013860.

import numpy as np

#determining the speed of light in water with a single measurement

#constant
c_air = 299702547 #m/s, speed of light in air

#measurements in meters
s2 = 0.29
s3 = 0.01
s4 = 0.3

#calculations
t_water = s4/c_air - s2/c_air
c_water = s3/t_water

#printing the solution to see clearly
print("The speed of light in water is:", c_water*1e-8, "*10^8 m/s")

The speed of light in water is: 2.997025469999997 *10^8 m/s

Python data-analysis example#

The code cell below shows a full data-analysis with some of the measurements as collected by Norbert van Veen. We introduced a systematic error as it could easily be that one of the measurements (for instance the distance determined without water) has a small measurement error.

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# example with multiple measurements

#constant
c_air = 299702547 #m/s, speed of light in air

#measurements in meters
s1 = np.array([30,30,60.2,60.2,60.2,60.2,30,30,40,40,40,40,65.1,66])*1e-2
s4 = np.array([30.2,30.5,61.2,61.8,62.8,63.85,31.1,31.8,40.1,40.4,41.3,41.9,67.4,68])*1e-2
s2 = np.array([29,28,53.5,52.5,51.5,57.3,26,24,39,38,36,34,60,57.7])*1e-2

#calculations
s3 = s1 - s2
t_water = (s4-s2)/c_air
c_water = s3/t_water

#printing the water array - uncomment if you want to use it
#print(c_water)

#using curve_fit to find the speed of light in water and a possible systematic error 
def c_w(t,c_w,sys_err):
    return c_w*t + sys_err

var, cov = curve_fit(c_w,t_water,s3)

#printing the values from the curve fit
print('the systematic error is:', var[1]) 
print('the calculated value is:', var[0]) 


#defining arrays to plot the fitted values against the measured values
x_test = np.linspace(min(t_water),max(t_water),1000)
y_test = c_w(x_test,*var)

#plot of the water depth versus t_water
plt.figure()

plt.plot(s3,t_water,'k.')
plt.plot(y_test,x_test,'r--')

plt.xlabel('$waterdepth$ (m)')
plt.ylabel('$t_{water}$ (s)')
plt.grid()

plt.show()

print('The speed of light in water is:',round(var[0]*1e-8,1),'+/-',round(np.sqrt(cov[0,0])*1e-8,1),'*10^8 m/s')

the systematic error is: -0.0007806756712641851
the calculated value is: 232127024.99422067

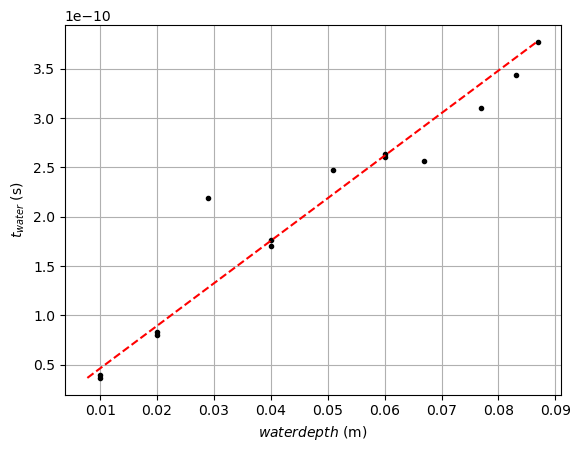
../../_images/d5765f017e65f1d328ff2972ab46eef2eb2804455d1e764d906013485a50c5c4.png

The speed of light in water is: 2.3 +/- 0.2 *10^8 m/s