Tension in a pendulum

17.14. Tension in a pendulum#

Author: Norbert van Veen
Time: 20-30 minutes
Age group: 14 - 18
Concepts: Tension, centripetal force
../../_images/demo66_figure1.jpg

Fig. 17.28 The setup with a ball attached to the force sensor.#

Introduction#

The pendulum experiment is often performed to determine the acceleration due to gravity \(g\) using the relationship between the length and the period of the pendulum. This demonstration is a variant of that. Students observe the measured force varying over time. To determine the oscillation period, students need to think about how the tension varies and how the position of the mass affects the magnitude of this tension.

Equipment#

  • Setup with stand and force sensor

  • Thin string

  • Measuring tape

  • Mass block (or ball)

  • Measurement interface

For this experiment we used Coach 7 to read out our device, however, many force measurement devices can be used.

Preparation#

  1. Start the software to read out your force sensor.

  2. Connect the force sensor to an interface and set it to the correct range.

  3. Attach the string to the force sensor and zero the sensor.

  4. Attach the mass block (or ball) to the string. See Figure 17.28 for the total setup.

  5. The force sensor will show a negative value. For didactic reasons, it is better to display this as a positive value. Create a new variable in a data table in which you multiply the force sensor value by -1.

Procedure#

  1. Let students calculate the mass based on the measured force of the stationary block.

  2. Optionally, show a graph of a harmonic oscillation (displacement versus time).

  3. Clearly explain that you are always measuring the tension in the string.

    • What direction does this force have?

    • How will the graph of tension versus time look when the block swings back and forth?

  4. Perform the measurement. Give the block a (small) displacement and press Start in Coach 7.

  5. Display the measured diagram (\(F_{\text{tension}}\) versus \(t\)) enlarged on the digital board.

    • In which position of the block is the tension minimal? And in which position is the tension maximal?

    • How can you read the oscillation period of this pendulum from the diagram and why does it need to be done this way?

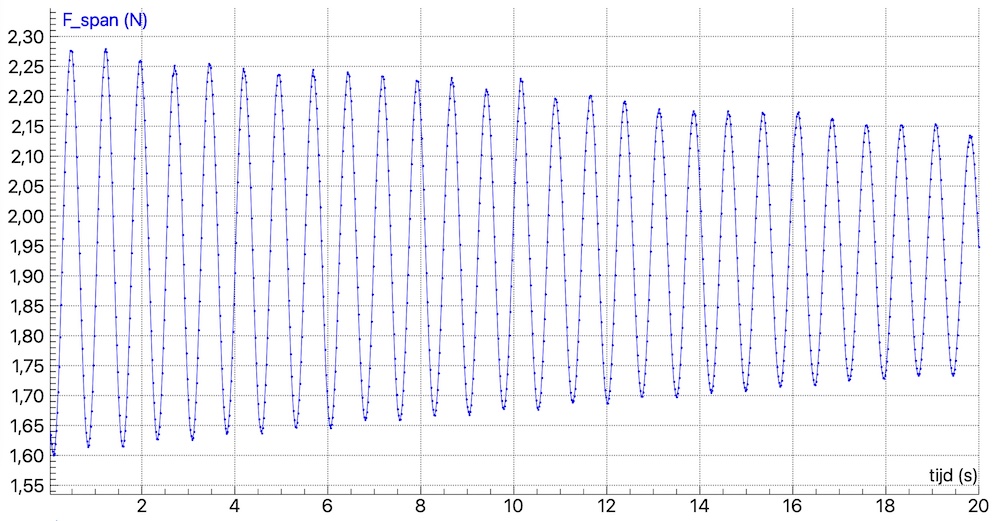
    ../../_images/demo66_figure2.jpeg

    Fig. 17.29 Measurements of the tension of a pendulum with a length of 0.55 m. Use the reading option in the diagram window of Coach 7 to read off the extreme values.#

  6. Let the students draw or sketch the force construction in the equilibrium position and in the extreme position of the pendulum.

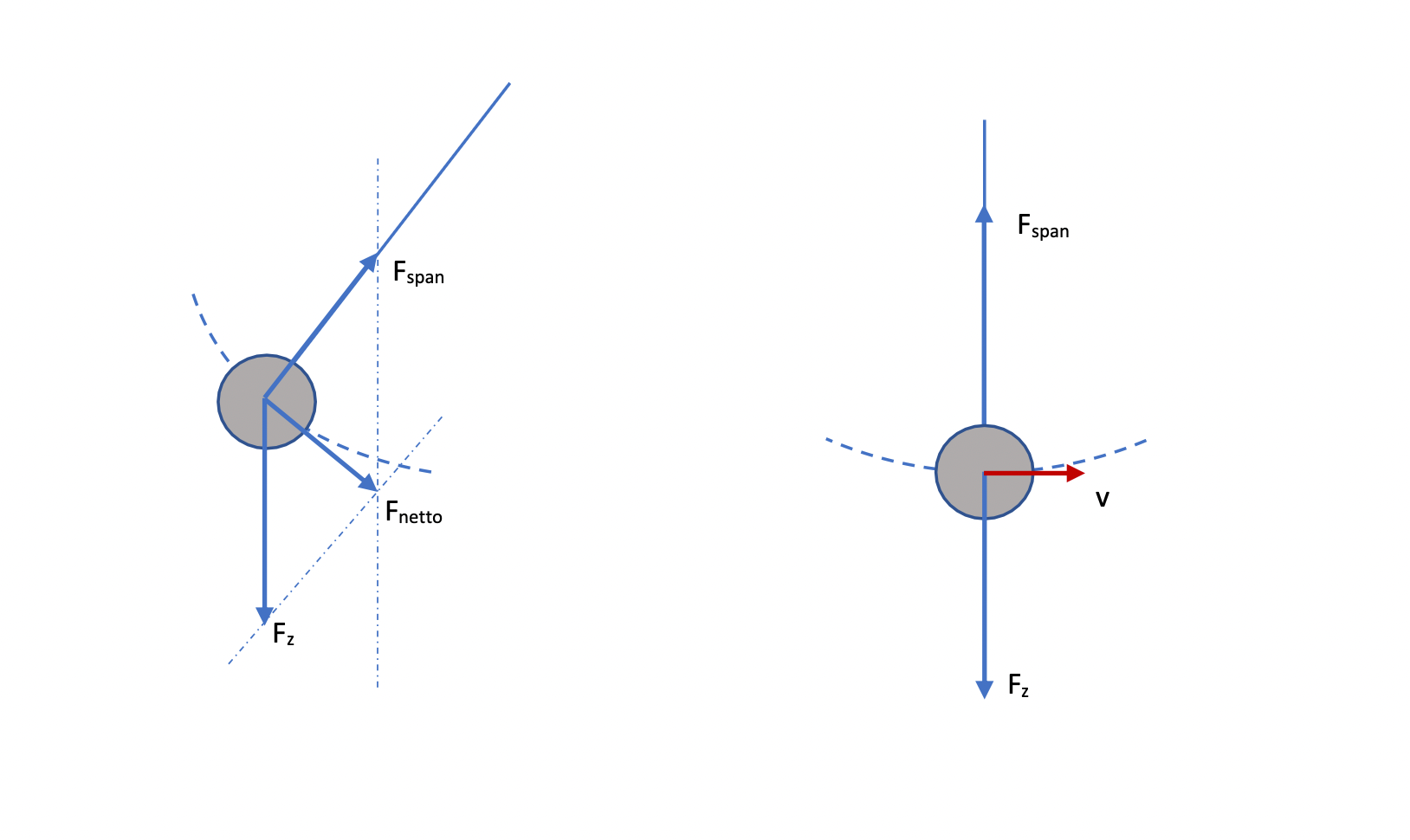
    ../../_images/demo66_figure3.png

    Fig. 17.30 Force construction in the extreme position and in the equilibrium position.#

  7. Have the students calculate the displacement angle in the extreme position.

  8. Students calculate the speed in the equilibrium position using the centripetal force.

  9. A question to check students’ understanding: When do you feel the “heaviest” while swinging? Why?

Physics background#

The length of the pendulum remains almost constant because the length of the strain gauge in the force sensor does not change for these tension values. The pendulum performs a harmonic oscillation if the displacement is small. The tension in the string is positive and does not change sign as the displacement does. In the extreme positions of the pendulum, the tension is minimal because the speed there is zero. In the equilibrium position, the tension is maximal because, in addition to compensating for gravity, it also provides the centripetal force. Through force constructions (equilibrium position and extreme position), students can see that the value of the tension changes as a function of the position of the block. Due to the symmetry of the pendulum, two minimal or two maximal values of the tension must be passed for one period of the pendulum. See also [Pendrill, 2023].

For further research you can use energy conservation laws to calculate the speed in the equilibrium position. Verify this speed using the centripetal force determined from the measured graph. Make a video measurement of the swinging block and verify your calculations using video measurement.

Tip

Ensure the hook of the force sensor is perpendicular to the loop of the string so that the block remains swinging in a plane.

References#

Pen23

Ann-Marie Pendrill. Serious physics on a playground swing—with toys, your own body, and a smartphone. The Physics Teacher, 61(5):355–359, 05 2023. doi:10.1119/5.0074171.

Contents