21. Relativistic dynamics and collisions

21.1. 4-force

In the previous chapter we have seen that 4-momentum is defined by taking the derivative of the 4-velocity with respect to proper time: \(P^\mu \equiv \frac{d U^\mu}{d \tau}\). This way, 4-momentum became a 4-vector that transforms according to the Lorentz Transformation.

In Special Relativity, we deal with inertial observers. The particles they encounter can, however, accelerate under the influence of forces. As momentum is now a 4-vector, we need to define a 4-force. Following Newton, momentum changes due to a force: \(\frac{d\vec{p}}{dt} = \vec{F}\). In chapter 2 we discussed Newton’s second Law in the form \(\vec{F} = m \vec{a}\). We saw that the acceleration did not provide any problems: we had rulers and clocks. Hence, we could measure the acceleration using know and measurable concepts like position, distance and time.

The connection between force and acceleration is of a different nature: it is a physical law, i.e. a formulation that reflects how we think nature works at its principle level. It is a hypothesis; something we need to check over and over. A rule that holds until we find inconsistencies: contradictions between theory and experiment. It takes only one experiment to overthrow a theory.

We postulate, that force is a 4-vector. Moreover, we require that in the limit of \(v/c \ll 1\), we recover Newton’s second Law from the spatial components of our new 4-vector force law. After all, for low velocities, Classical Mechanics of Newton and Galilei works like a charm. This indicates that we need to differentiate 4-momentum with respect to time. But, if we require force to be a 4-vector, we need to differentiate with respect to proper time. Thus, we postulate:

\[ \vec{F}=\frac{d\vec{P}}{d\tau}= \gamma(u)\frac{d}{dt}\left ( m\gamma(u)c,m\gamma(u)\vec{u}\right ) \]

with \(E=m\gamma(u)c^2\) we can rewrite this to

\[ \vec{F} = \gamma(u) \left ( \frac{1}{c}\frac{dE}{dt}, \frac{d}{dt}m\gamma(u)\vec{u} \right ) = \gamma(u) \left ( \frac{1}{c}\frac{dE}{dt}, \vec{f} \right ) \]

with the 3-force \(\vec{f}= \frac{d}{dt}(m\gamma(u)\vec{u})\)

21.1.1. Work and Impulse

How about our ideas of force performing work by that force acting over a distance or providing momentum by a force working during a time interval? These ideas and concepts still apply, but they take a relativistic form. Let’s see how that works.

First, the natural extension of the definition of work is now:

\[dW = F^\mu dX^\mu \]

If we repeat what we did in chapter 4, we will replace \(dX^\mu\) by \(U^\mu \equiv \frac{dX^\mu}{d\tau}\) and instead of \(F^\mu\) we write \(\frac{dP^\mu}{d\tau}\):

\[\begin{split}\begin{split} dW &= F^\mu dX^\mu \\ &= \frac{dP^\mu}{d\tau} U^\mu d\tau \\ &= m \frac{dU^\mu}{d\tau} U^\mu d\tau \\ &= mU^\mu d U^\mu \\ &=\frac{1}{2}m \ d \left ( U^\mu U^\mu \right ) \end{split}\end{split}\]

However, \(U^\mu U^\mu = \gamma^2 c^2 - \gamma^2 \vec{u}\cdot \vec{u} = c^2\). That is, it is a constant (for all inertial observers the same). Thus \( d U^\mu U^\mu \) = 0. And we must conclude that

\[dW = F^\mu dX^\mu = 0\]

Surprisingly, 4-force does perform zero work, always?! It is, on second thought, less surprising. Let’s see how it works out in terms of 4-momentum:

\[\begin{split}\begin{split} 0 = dW &= F^\mu dX^\mu \\ &= \frac{dP^\mu}{d\tau} dX^\mu \\ &= \gamma \frac{dP^0}{dt} cdt - \gamma \frac{dP^1}{dt} u_xdt - \gamma \frac{dP^2}{dt} u_ydt - \gamma \frac{dP^3}{dt} u_zdt \\ &= \gamma \frac{dE/c}{dt} c - \gamma \vec{u} \cdot \frac{d \gamma m \vec{u}}{dt} \end{split}\end{split}\]

Thus we can divide \(\gamma\) out of this equation and write \(c E/c = E\):

\[0 = \frac{dE}{dt} - \vec{u} \cdot \frac{d \gamma m \vec{u}}{dt} \Rightarrow \frac{dE}{dt} = \vec{u} \cdot \frac{d \gamma m \vec{u}}{dt}\]

But this is the relativistic equivalent of

\[ \mathcal{P} \equiv \frac{dE}{dt} = \vec{f} \cdot \vec{u}\]

In words: the inner product of 3-force and 3-velocity is the power \(\mathcal{P}\).

21.2. Collisions

We will now concentrate on collisions. From our earlier discussions, for collisions we assume that we can look ‘over’ the collision, that is: we applied conservation of momentum and -for elastic collisions- kinetic energy. The latter implies: no non-conservative forces that dissipate mechanical energy and the potential energy prior and after the collision is the same. We do that also for our relativistic collisions. But, we don’t require that it only holds for perfectly elastic collisions. Instead, we apply it to cases where there is no possibility to turn some of the energy involved into heat. So, we focus on collisions of elementary particles that do not convert part to their energy to heat.

The 4-momentum is conserved.
For \(\vec{P}=(\frac{E}{c},\vec{p})\) we have

\[ \sum_{i,before} \vec{P}_i = \sum_{j,after} \vec{P}_j \]

and the energy-momentum relation from the LT invariance of \(\vec{P}\cdot\vec{P}\)

\[ E^2 = (mc^2)^2 + (pc)^2 \]

With \(E=m\gamma(u)c^2\) and \(\vec{p}=m\gamma(u)\vec{u}\).

21.2.1. Example: head on collision

Two elementary particles collide

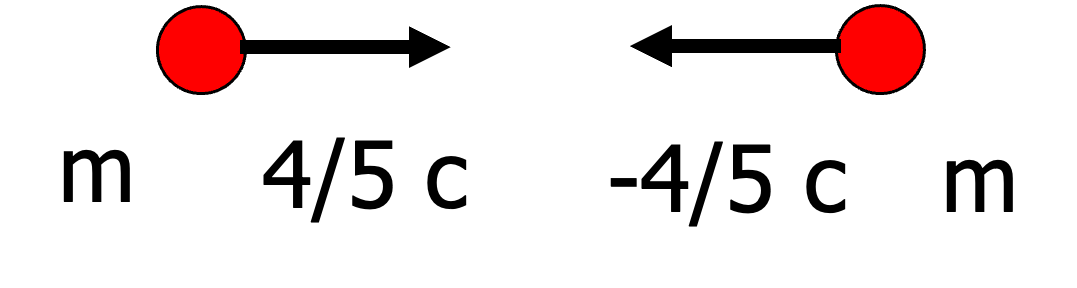
Both particles have mass \(m\), after the collision there is only one particle with unknown mass \(M\). What is the mass \(M\) and the velocity \(v\) of the one particle after the collision/fusion?

We consider the conservation of 4-momentum, in 1D:

\[\begin{split} \begin{array}{rcl} P_{before}^\mu &=& (m\gamma(u)c,m\gamma(u)u)+(m\gamma(-u)c,-m\gamma(-u)u)\\ &=& (2m\gamma(u)c,0)\\ P_{after}^\mu &=& (M\gamma(v)c,M\gamma(v)v) \end{array} \end{split}\]

with \(\gamma(u)=\gamma(-u)\). The 4-momentum is conserved per component, from the space component we see \(0=M\gamma(v)v\Rightarrow v=0\). With \(\gamma(u)=5/3\) and \(\gamma(v)=1\) we find for the time-component \(2m\frac{5}{3}=M\).

This leads to \(M=\frac{10}{3}m > 2m\). Thus, the energy prior to the collision was composed of energy associated with the masses themselves and with kinetic energy. After the collision, there is no kinetic energy but their is mass-energy and there is more of this than prior to the collision.

21.2.2. Example: decay of a photon into an electron and positron

We discuss if a photon (of sufficient energy \(E>1024\) keV) can decay into an electron \(e^-\) and positron \(e^+\).

If we place us in the Center of Mass (CM) frame of the electron \(e^-\) and positron \(e^+\) after the decay, then the total spatial momentum is \(\vec{p}=0\). The momentum before the decay of the photon is \(\vec{p}=\frac{hf}{c}>0\) therefore the decay cannot happen in free space. Momentum must be transferred to an additional different particle.

\[ \left ( \frac{E_e}{c},\vec{p} \right ) + \left ( \frac{E_p}{c},-\vec{p} \right ) \neq \left ( \frac{hf}{c},\frac{hf}{c} \right ) \]

21.2.3. Example: Electron positron annihilation

We consider an electron and positron annihilation, resulting in two photons (after the collision). Remember that the decay cannot happen into one photon as shown above (Remember: equations are invariant under time reversal).

In the CM of the \(e^-e^+\) system we have for the 4-momentum before

\[ P_{before}^\mu =(m_e \gamma(u)c, m_e \gamma(u)u,0,0)+ (m_e \gamma(-u)c, -m_e \gamma(-u)u,0,0) \]

After we have two photons, with different frequencies \(f,f'\) and traveling in different directions \(\hat{s},\hat{s}'\)

\[ P_{after}^\mu = \left ( \frac{hf}{c}, \frac{hf}{c} \hat{s}\right ) + \left ( \frac{hf'}{c}, \frac{hf'}{c}\hat{s}'\right ) \]

From the conservation of 4-momentum we have

\[\begin{split} \begin{array}{rcl} 2m_e\gamma(u) c &=& \frac{hf}{c}+\frac{hf'}{c}\\ 0 &=& \frac{hf}{c}\hat{s} + \frac{hf'}{c}\hat{s}' \end{array} \end{split}\]

From the second equation we see

\[ \frac{hf}{c}\hat{s} = -\frac{hf'}{c}\hat{s}' \Rightarrow \hat{s} = -\hat{s}',\quad f=f' \]

The two photons are emitted in opposite directions (in the CM system) with the same frequency.

Filling this into the first equation \(hf = m_e \gamma(u)c^2 \approx m_e c^2 = 512\) keV. The speed in the CM frame is typically \(u\ll c \Rightarrow \gamma(u)=1\).

NB: please observe that analysis in the CM frame is often a good idea.

21.2.4. Example: Compton scattering

Compton scattering describes the (elastic) scattering of an incoming photon by a (bound) charged particle, typical an electron.

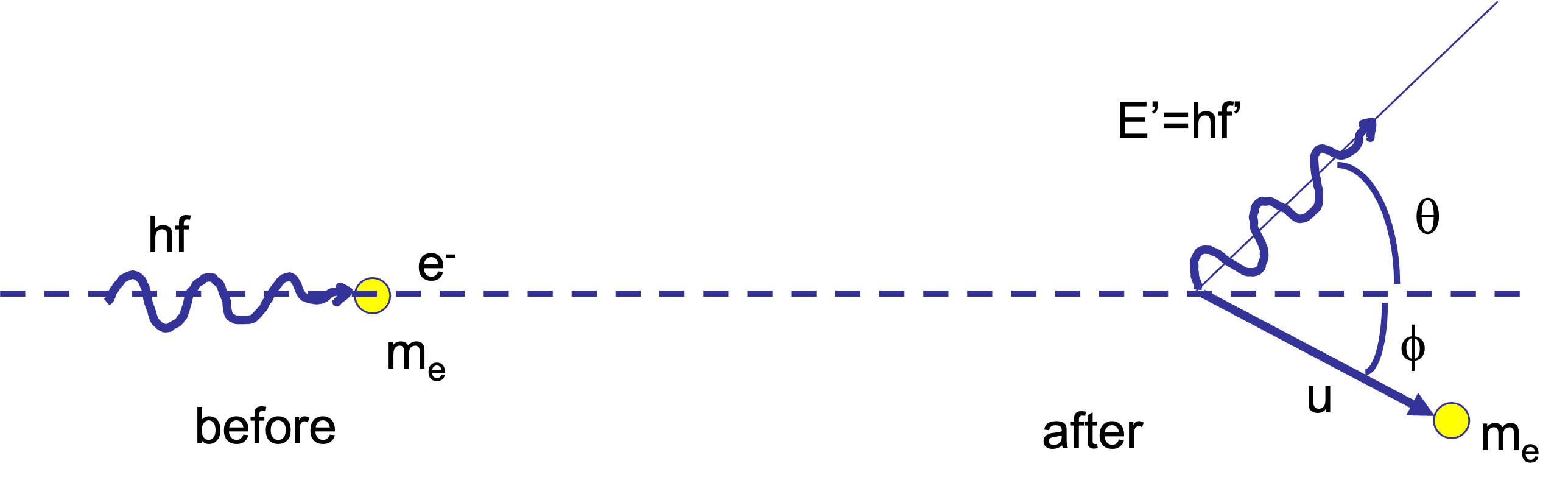
Fig. 21.1 Compton scattering of a photon by an electron

In the rest frame of the electron, we have for the 4 different 4-momenta:

\[\begin{split} \begin{array}{rcl} P_{e,b} &=& (m_e c,0,0,0)\\ P_{\gamma, b} &=& (E/c,E/c,0,0)\\ P_{e,a} &=& (\frac{E_e'}{c},m_e\gamma(u)u \cos\phi, -m_e \gamma(u)u \sin \phi,0)\\ P_{\gamma,a} &=& (\frac{E'}{c}, \frac{E'}{c} \cos\theta, \frac{E'}{c}\sin\theta,0) \end{array} \end{split}\]

We have

\[ P_{e,b} + P_{\gamma, b} = P_{e,a} + P_{\gamma,a} \]

Now we make use of the LT invariance of \(\vec{P}^2\)

\[ (P_{e,b} + P_{\gamma, b} - P_{\gamma,a})^2 = P^2_{e,a} \]

\[ P_{e,b}^2 + P_{\gamma, b}^2 + P_{\gamma,a}^2 + 2P_{e,b}P_{\gamma, b} - 2P_{e,b}P_{\gamma,a} - 2P_{\gamma, b}P_{\gamma, a} = P^2_{e,a} \]

where we know \(P^2_{e,b}=P^2_{e,a} = m_e^2c^2\) (totally elastic collison) and \(P_\gamma^2=0\) directly as shown before. Evaluating the cross terms gives

\[ m_e^2c^2 +0+0+2m_eE'-2m_eE-2 \frac{EE'}{c^2}(1-\cos\theta)=m_e^2c^2 \]

We isolate the energy after the collision \(E'\)

\[ E' = \frac{Em_ec^2}{m_ec^2 +E(1-\cos\theta)} \]

With \(E=hc/\lambda\) we obtain

\[ \frac{\lambda'}{hc} = \frac{m_ec^2 +\frac{hc}{\lambda}(1-\cos\theta )}{\frac{hc}{\lambda} m_ec^2} \]

Now we only multiply both sides by \(hc\) and on the right we divide out, to obtain

\[ \lambda' = \lambda + \frac{h}{m_ec}(1-\cos\theta) \]

Alternatively, we could try and solve the collision by directly using conservation of momentum. This is much more work than the \(P^2\) trick. The calculation goes as follows.

In the rest frame of the electron

\[ P_{before}^\mu = \left ( \frac{hf}{c},\frac{hf}{c},0,0 \right ) +(m_e c,0,0,0) \]

After the scattering

\[\begin{split}\begin{split} P_{after}^\mu = &\left ( \frac{hf'}{c},\frac{hf'}{c} \cos\theta, \frac{hf'}{c} \sin\theta,0 \right ) + \\ & + \left ( m_e\gamma(u)c,\, m_e\gamma(u)u \cos\phi,\, -m_e \gamma(u) u\sin\phi,\,0 \right ) \end{split}\end{split}\]

We have 3 equations, but 4 unknowns \((f', u, \phi, \theta)\). Therefore the outgoing frequency \(f'\) is not uniquely determined, but dependent on the scattering angle \(\theta\). We can eliminate 2 (here \(u,\phi\)) of the 4 unknowns, to remain with a relation for the other two.

For the spatial momentum we have

\[\begin{split} \begin{array}{rcl} \frac{hf}{c} &=& \frac{hf'}{c}\cos\theta + m_e \gamma(u)u\cos\phi\\ 0 &=& \frac{hf'}{c}\sin\theta - m_e \gamma(u)u\sin\phi \end{array} \end{split}\]

We rewrite the equations slightly, before squaring them and then adding them to eliminate \(\phi\)

\[\begin{split} \begin{array}{rcl} \frac{hf}{c} - \frac{hf'}{c}\cos\theta&=& m_e \gamma(u)u\cos\phi\\ \frac{hf'}{c}\sin\theta &=& m_e \gamma(u)u\sin\phi \end{array} \end{split}\]

We indeed eliminate \(\phi\) to

\[ \frac{h^2f^2}{c^2}-2\frac{hfhf'}{c^2}\cos\theta + \frac{h^2 f'^2}{c^2}=m_e^2 \gamma^2(u)u^2 \quad (*) \]

The right hand side of the equation is the space component squared of the momentum after: \(p^2_{e'} = m_e^2\gamma^2(u)u^2\), but this can be related to the energy via the momentum-energy relation for the moment after \((p_{e'}c)^2 = E^2_{e'}-(m_ec^2)^2\). We will use this to eliminate the unknown speed \(u\).

The energies can be related via the 0-component of the 4-momentum

\[\begin{split} \begin{array}{rcl} \frac{hf}{c}+m_e c &=& \frac{hf'}{c} + \frac{E'_e}{c}\\ \Rightarrow E^{'2}_e &=& (hf-hf'+m_ec^2)^2 \end{array} \end{split}\]

Substituting the energy \(E^{'2}_e\) into the momentum-energy relation and replacing the right hand side of equation \((*)\) after multiplying by \(c^2\) to

\[ h^2f^2-2hfhf'\cos\theta + h^2 f'^2= (hf-hf'+m_ec^2)^2 - (m_ec^2)^2 \]

Indeed we have removed the speed \(u\) and angle \(\phi\). We cannot do more, but remain with a relation for the frequency \(f'\) after scattering as function of angle \(\theta\). To this end we evaluate the square in the equation, cancel a few terms and rearrange to

\[\begin{split} \begin{array}{rcl} 2hfm_ec^2 - 2hf'm_ec^2 &=& 2h^2 ff' (1-\cos\theta)\\ \frac{c}{f'}-\frac{c}{f} &=& \frac{h}{m_ec}(1-\cos\theta) \end{array} \end{split}\]

Finally, by replacing the frequency with the wavelength \(f\lambda=f'\lambda'=c\)

\[ \lambda'-\lambda = \frac{h}{m_ec}(1-\cos\theta) \]

This is, of course, the same result as we derived earlier.

As \(\cos\theta<1\) we find \(\lambda'>\lambda\), which makes sense as the photon can only loose energy to the electron in the initial rest frame of the electron. After the scattering the electron can pick up some speed.

To analyze the outcome we check for

• \(\theta=0\) (no scattering): \(\Rightarrow \lambda'=\lambda\) which makes sense

• \(\theta=\pi\): backwards scattering, maximal \(\Delta \lambda = \frac{2h}{m_ec}\) largest energy transfer

21.3. Exercises

Exercise 21.1

A particle of mass \(M\) disintegrates into two fragments. In the rest frame of \(M\), fragment \(m_1\) has a mass of \(\frac{1}{4}M\) and a velocity \(u_1 /c = 3/5\).

Find the mass and velocity of the other fragment.

Exercise 21.2

A particle of mass \(m\) is initially at rest (in frame \(S\)). A photon of frequency \(f\) is traveling over the \(x\)-axis and will be absorbed by the particle. Subsequently, another photon is emitted. This photon is also traveling over the \(x\)- axis but in the opposite direction as the incoming photon.

The incoming photon energy equals \(mc^2\), the emitted photon \(\frac{1}{4}mc^2\). Find the velocity and mass of the particle after the process of absorbing and emitting the photons.

Exercise 21.3

An elementary particle of mass \(M\) moves in the frame of observer \(S\) with a velocity \(v/c = 12/13\). The particle is unstable and decays into a particle of mass \(m\) and a photon. The particle \(m\) has velocity \(u/c = 4/5\). Both \(M\) and \(m\) move along the \(x\)-axis in the positive direction.

a. Find the mass \(m\) in terms of \(M\).
b. What is the frequency of the photon?

Exercise 21.4

A particle of mass \(m\) moves with velocity \(v_1 /c = 1/2\) in the positive direction over the \(x\)-axis. At the same time, an identical particle is moving with the same velocity in the positive \(y\)-direction over the \(y\)-axis. At some point in time the two particles collide and as a result a new particle of mass \(M\) is formed.

Find the mass and velocity-vector of the new particle.

Exercise 21.5

A particle of mass \(\frac{3}{5}m\) is moving at velocity \(v_1/c = 4/5\) over the \(x-axis\). From the other side a particle with mass \(\frac{4}{5}m\) is approaching with velocity \(v_2/c = 3/5\). The two particles will collide. After the collision, they maintained each their original mass. The collision is perfectly elastic.

a. Find the velocities of both masses in the world of Galilei and Newton.
b. The same but now in the world of Lorentz and Einstein.

21.3.1. Answers

Solution to Exercise 21.1

Prior to the disintegration, particle \(M\) has 4-momentum:

\[P_i^\mu = \left ( Mc, 0 \right )\]

After the disintegration, we have two particles with 4-momentum:

\[P_{1,a}^\mu = \left ( \frac{1}{4}M \frac{5}{4}c, \frac{1}{4}M \frac{5}{4}\frac{3}{5}c \right )\]

and

\[P_{2,a}^\mu = \left ( m_2 \gamma_2 c, m_2 \gamma_2 u_2 \right )\]

From conservation of momentum we get:

\[\begin{split}\begin{split} 1 &= \frac{5}{16} + \frac{m_2}{M} \gamma_2 \rightarrow \frac{m_2}{M} \gamma_2 = \frac{11}{16}\\ 0 &= \frac{3}{16} + \frac{m_2}{M} \gamma_2 \frac{u_2}{c} \rightarrow \frac{m_2}{M} \gamma_2 \frac{u_2}{c} = -\frac{3}{16} \end{split}\end{split}\]

Take the ratio of the last two equations:

\[\frac{u_2}{c} = -\frac{3}{11}\]

and from this we find

\[\frac{m_2}{M} = \frac{4\sqrt{7}}{16}\]

Thus, we see that the mass after the disintegration is \(\frac{1}{4}M + \frac{4\sqrt{7}}{16}M \approx 0.911 \lt M\).

Solution to Exercise 21.2

Before the absorption of the photon the 4-momentum is:

\[P_i^\mu = \left ( \frac{hf}{c}, \frac{hf}{c}\right) + \left ( mc, 0 \right ) = \left ( 2mc, mc \right )\]

After emitting the photon, the particle has mass \(M\) and velocity \(u\). The emitted photon has as frequency \(\tilde{f}\) and 4-momentum \(\left ( \frac{h\tilde{f}}{c}, -\frac{h\tilde{f}}{c} \right ) = (\frac{1}{4}mc, -\frac{1}{4}mc) \). The total momentum after the process is:

\[P_f^\mu = \left ( \frac{1}{4}mc + M \gamma c, -\frac{1}{4}mc + M \gamma u \right )\]

Since 4-momentum is conserved, we find:

\[\begin{split}\begin{split} 2mc &= \frac{1}{4}mc + M \gamma c \\ mc &= -\frac{1}{4}mc + M \gamma u \end{split}\end{split}\]

We rearrange the two above equations:

\[\begin{split}\begin{split} M \gamma c &= \frac{7}{4}mc \\ M \gamma u &= \frac{5}{4}mc \end{split}\end{split}\]

If we divide the second equation by the first, we have:

\[ \frac{u}{c} = \frac{5}{7} \]

The mass of the particle is:

\[M = \frac{7}{4 \gamma }m = \frac{1}{2} \sqrt{6} \,m\]

Solution to Exercise 21.3

Initially, the 4-Momentum is

\[P^\mu_i = \left ( M\gamma(v) c, M\gamma(v) v\right ) \]

with $\(\frac{v}{c} = \frac{12}{13} \rightarrow \gamma(v) = \frac{13}{5} \)$

After the decay, we have

\[P^\mu_f = \left ( m\gamma(u) c + \frac{hf}{c}, m\gamma(u) u + \frac{hf}{c} \hat{f}\right ) \]

with \(\hat{f}\) a unit vector pointing in the \(\pm x\)-direction. We know \(\frac{u}{c} = \frac{4}{5} \rightarrow \gamma(u) = \frac{5}{3}\). Conservation of 4-momentum now leads to::

\[\begin{split}\begin{split} \frac{5}{3}mc +\frac{hf}{c} &= \frac{13}{5}Mc \\ \frac{4}{3}mc \pm \frac{hf}{c} &= \frac{12}{5}Mc \end{split}\end{split}\]

We still need to find out which direction the photon travels: parallel to \(m\) or in the opposite direction. According to the above conservation of 4-momentum both seem possible. We must require that in the above \(f \gt 0\), otherwise the energy of the photon would be negative. Rephrased: the direction of the photon is given via the sign of \(\hat{f}\).

First we inspect the negative sign of \(\pm\):

\[\begin{split}\begin{split} \frac{5}{3}mc +\frac{hf}{c} &= \frac{13}{5}Mc \\ \frac{4}{3}mc - \frac{hf}{c} &= \frac{12}{5}Mc \end{split}\end{split}\]

If we solve for \(f\), we get \(f \lt 0\), which conflicts our requirement. That leaves us with the \(+\)sign:

\[\begin{split}\begin{split} \frac{5}{3}mc +\frac{hf}{c} &= \frac{13}{5}Mc \\ \frac{4}{3}mc + \frac{hf}{c} &= \frac{12}{5}Mc \end{split}\end{split}\]

Solving for \(m\) gives: \(m = \frac{3}{5}M\). If we plug this back in, we find for the photon \(hf = \frac{8}{5}Mc^2\).

Solution to Exercise 21.4

The total 4-momentum before the collision is

\[P_i^\mu = \left ( 2m\gamma c, \frac{1}{2} m\gamma c, \frac{1}{2} m\gamma c \right ) \text{ with } \gamma = \frac{2}{3} \sqrt{3}\]

After the collision, we have only one particle with 4-momentum

\[P_f^\mu = \left ( M \gamma_f c, M\gamma_f u_x, M\gamma_f u_y \right ) \text{ with } \gamma_f = \frac{1}{\sqrt{1 - \frac{u_x^2 + u_y^2}{c^2}}} \]

In this process, 4-momentum is conserved.

From \(P^1\) and \(P^2\) we get

\[\begin{split}\begin{split} \frac{1}{2} m\gamma c &= M\gamma_f u_x \\ \frac{1}{2} m\gamma c &= M\gamma_f u_y \end{split}\end{split}\]

hence, \(u_x = u_y\). The new particle moves over the line \(x=y\).

If we combine \(P^0\) with \(P^1\), we find:

\[\begin{split}\begin{split} 2 m\gamma c &= M\gamma_f c \\ \frac{1}{2} m\gamma c &= M\gamma_f u_x \end{split}\end{split}\]

This gives \(\frac{u_x}{c} = \frac{1}{4}\). Thus the new particle moves with velocity \(\vec{u} = \frac{1}{4}c \hat{x} + \frac{1}{4}c \hat{y}\). We find its mass by calculating \(\gamma_f = \frac{1}{\sqrt{1-2\frac{1}{16}}} = 2\sqrt{\frac{2}{7}} \) and using this in the \(P^0\) equation:

\[ 2m\gamma c = M\gamma_f c \rightarrow M = \sqrt{\frac{14}{3}}m \]

Solution to Exercise 21.5

a. In classical mechanics, we use -for this type of collision- conservation of momentum and of kinetic energy. This gives us:

\[\begin{split}\begin{split} p: \,\,\,\,\frac{3}{5}m \frac{4}{5}c - \frac{4}{5}m \frac{3}{5}c &= \frac{3}{5}m u + \frac{4}{5}m U \rightarrow U = -\frac{3}{4}u\\ E_{kin}: \,\,\,\,\, \frac{1}{2}\frac{3}{5}m \left (\frac{4}{5}c \right )^2 + \frac{1}{2}\frac{4}{5}m \left (\frac{3}{5}c \right )^2 &= \frac{1}{2}\frac{3}{5}m u^2 + \frac{1}{2}\frac{4}{5}m U^2 \end{split}\end{split}\]

This set has as solution (not surprising): \(u = -\frac{4}{5}c, U = \frac{3}{5}c\).

b. Now we use 4-momentum conservation:

\[P_i^\mu = \left ( \frac{3}{5}m \frac{5}{3}c, \frac{3}{5}m \frac{5}{3}\frac{4}{5}c \right ) + \left ( \frac{4}{5}m \frac{5}{4}c, -\frac{4}{5}m \frac{5}{4} \frac{3}{5}c \right ) = \left ( 2mc, \frac{1}{5}mc \right ) \]

Note: the spatial part of momentum is thus non-zero, in contrast to the classical case.

After the collision we have:

\[P_f^\mu = \left ( \frac{3}{5}m \gamma_1 c, \frac{3}{5}m \gamma_1 u \right ) + \left ( \frac{4}{5}m \gamma_2 c, -\frac{4}{5}m \gamma_2 U \right ) \]

with

\[ \gamma_1 = \frac{1}{\sqrt{1-\frac{u^2}{c^2}}} \text{ and } \gamma_2 = \frac{1}{\sqrt{1-\frac{U^2}{c^2}}}\]

Next, we use conservation of 4-momentum: \(P_i^\mu = P_f^\mu\). This is, however, hard to do analyticalyl! Thus we use either a graphical or numerical method. If you do this, you will find:

\[u = - 0.7355c \text{\;\;\;\;\; and \;\;\;\;\; } U = + 0.8050 c\]