Collisions

10. Collisions#

10.1. What is it?#

In daily life we do understand what a collision is: the bumping of two objects into each other.

From a physics point of view, we see it slightly different. The objects don’t have to touch. It is sufficient if they undergo a mutual interaction ‘with a beginning and an end’. What do we mean by this? Firstly, the mutual interaction means that the objects interact with each other through a mutual force, i.e. a force (pair) that obeys Newton’s third law.

Secondly, we assume that this force works over a small distance only. Or re-phrased we will only consider the situation before the objects feel the force and compare that to after they have felt it. We don’t bother about the details of the motion of the objects during their interaction. Hence, when we depict a collision, we usually draw the situation before the collision, then some kind of ‘comic way’ of showing the collision and finally we draw the outcome of the collision, so after the interaction. In many case, people leave the middle part out of their drawing.

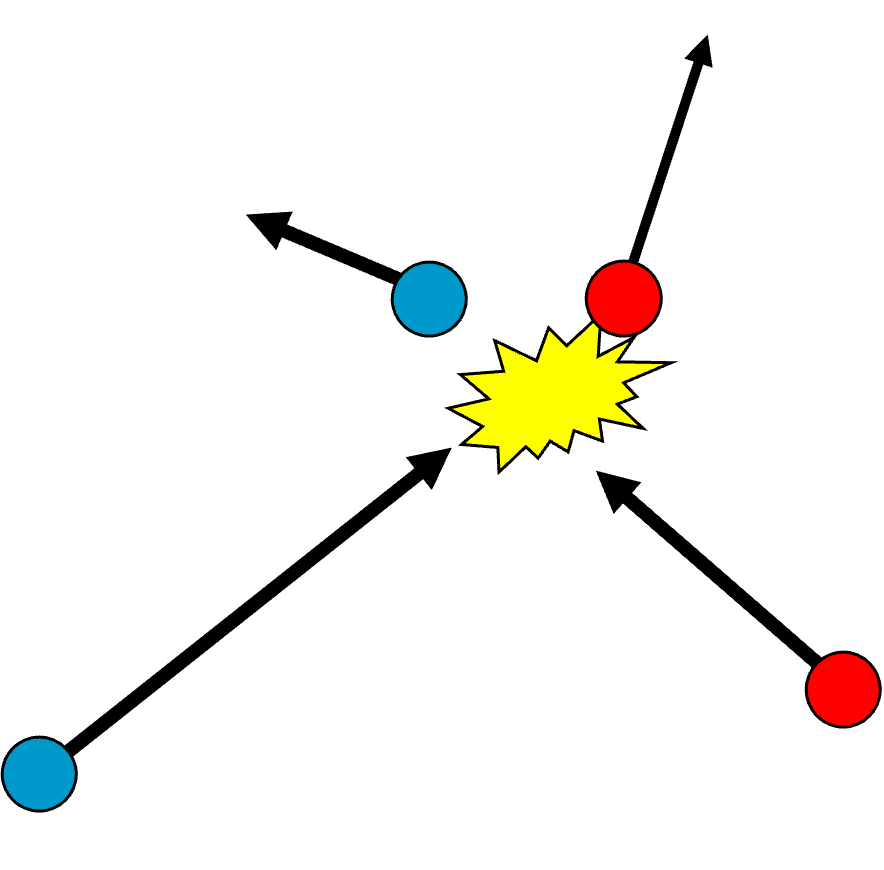
../_images/collision.png — Fig. 10.1 Collision of two particles.#

There are two principle type of collisions to distinguish: elastic and inelastic collisions. For an elastic collision the kinetic energy is conserved, whereas for an inelastic that is not the case. In the latter case, energy can be converted into deformation or heat.

Since the objects interact under the influence of their mutual interaction, we have conservation of momentum: $$ \sum_i \vec{p}_i^{before} = \sum_i \vec{p}_i^{after} $$

Why: no external forces implies constant total momentum.

10.2. Elastic Collisions#

For an elastic collision the kinetic energy is conserved by definition next to the momentum. That is the sum of the kinetic energy before the collision is the same as the sum after the collision. This type of collision is also called hard-ball collision; no energy is dissipated into heat or deformation. Think off colliding billiard balls.

For this to be possible, we need to have that the interaction force is conservative. Then, a potential energy exists. And this energy is such that the objects have the same potential energy before as after the collision. Consequently energy conservation leads to:

\[ E_{kin, before} + V_{before} = E_{kin, after} +\underbrace{V_{after}}_{= V_{before}} \Rightarrow E_{kin, before} = E_{kin, after} \]

10.2.1. Solving strategy#

Here we explain how to compute the velocities after the collision, given the initial situation before the collision. We show this by an example. Consider a head-on collision of two point particles on a line as shown in the figure.

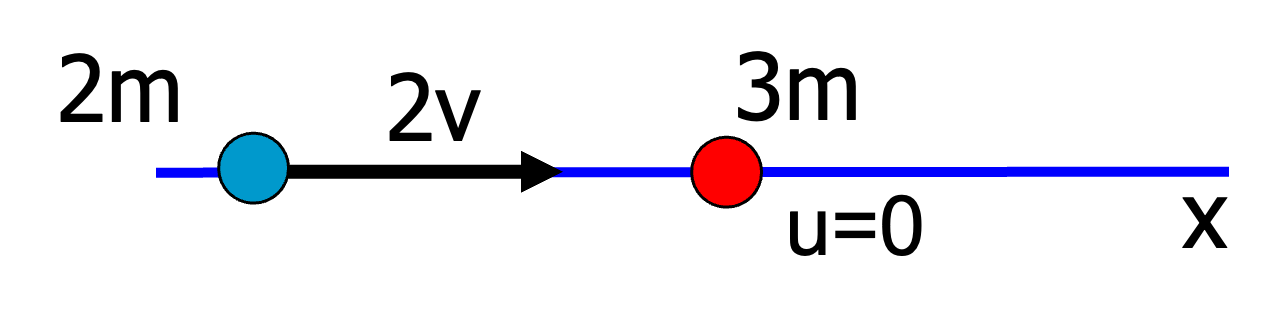
../_images/collision2.png — Fig. 10.2 Example of a 1D elastic collision.#

One particle with mass $3m$ is initially at rest ($u=0$), the other with mass $2m$ has velocity $v$. What are the velocities $v',u'$ of the particles after the collision?

We can write down two equations using conservation of momentum and kinetic energy before and after the collision

\[\begin{split} \begin{array}{rcl} 2m2v+0 &=& 2mv' + 3mu' \quad (*)\\ \frac{1}{2}2m(2v)^2 + 0 &=& \frac{1}{2}2mv'^2 + \frac{1}{2} 3mu'^2 \end{array} \end{split}\]

We have 2 equation and 2 unknowns $(v',u')$, therefore we can always solve this problem. The question is, what is the best strategy to do so? One equation involves the square of the velocity therefore a good strategy will help. We first bring the velocities $v,v'$ and $u,u'$ to the same side.

\[\begin{split} \begin{array}{rcl} 2m(2v-v')&=& 3mu'\\ \frac{1}{2}2m(4v^2-v'^2) &=& \frac{1}{2}3mu'^2 \end{array} \end{split}\]

Now we divide the two equations, this makes the solution very easy as the squares of the velocities always divide out.

\[ \Rightarrow 2v+v'=u' \quad (**) \]

We can use this to find both unknowns by adding equations $(*)$ and $(**)$

\[\begin{split} \begin{array}{lcl} 4v=2v'+3u' && 4v=2v'+3u'\\ 2v=-v'+u'|\cdot 2 && 2v=-v'+u'|\cdot -3 \\ \end{array} \end{split}\]

\[ \begin{array}{lcr} 8v=5u' \Rightarrow u'=\frac{8}{5}v && -2v=5v' \Rightarrow v'=-\frac{2}{5}v \end{array} \]

This solution strategy always works. NB: you need to practice this. Although it is conceptually easy, we often see that students have problems when actually solving for the 2 unknowns.

Actually, now we think about this strategy: isn’t it strange, the kinetic energy equation is squared in our unknowns. Shouldn’t we expect 2 solutions?

The answer is yes: there ought to be 2 solutions. Where is the second one? Note that when dividing the two equations, we have to make sure that we don’t divide by 0. That is very well possible that we do so: suppose $u' = 0$, then also $2v-v' = 0$ and we can not do the division. But what does that mean: $u'=0$ and $2v-v'=0$? Well, of course, then we have after the collision that the incoming particle $2m$ still has velocity $2v$ and the other particle $3m$ is still at rest.

In retrospect: of course this must be one of the solutions to the problem. We haven’t specified anything about the interaction force. But suppose it is absent, that is the particles don’t feel each other at all. Then of course the situation before the collision (a bit strange calling this a collision, but anyway), will still be present after the ‘collision’. If nothing happens to the particles, then obviously the sun of the momentum as well as of the kinetic energy stays the same. This actually provides a great check of your work: do you recover the initial conditions?

10.2.2. Collisions in the plane#

Consider now a 2D collision such that the two particles collide in the origin.

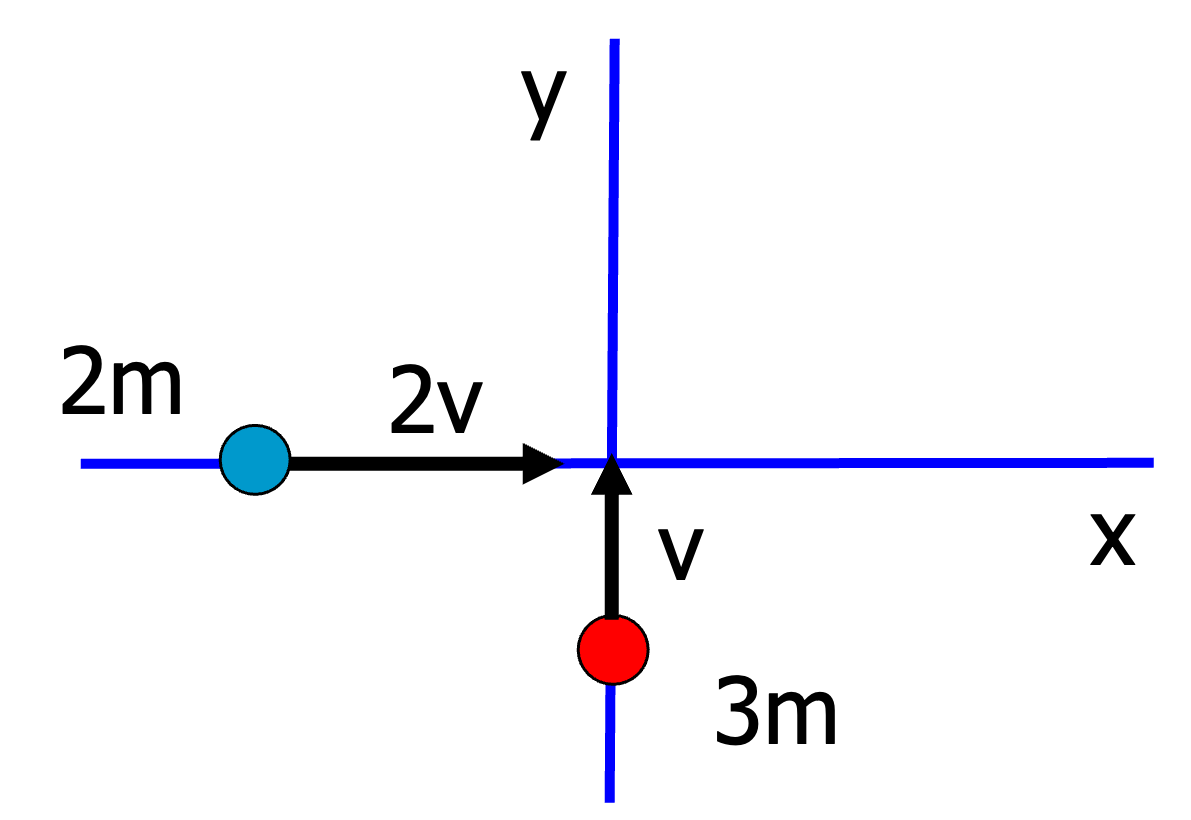
../_images/collision2D.png — Fig. 10.3 Example of a 2D elastic collision.#

If we write down the equation of conservation of momentum (in $x,y$ components) and of kinetic energy

\[\begin{split} \begin{array}{lcr} x-momentum:\;\;\;\;\;\;\;\;\;\; 2m2v+0 &=& 2mv'_x + 3mu'_x \\ y-momentum:\;\;\;\;\;\;\;\;\;\; 0+ 3mv &=& 2mv'_y + 3mu'_y \\ Ekin:\;\;\;\;\;\;\;\;\;\;\frac{1}{2}2m(2v)^2 + \frac{1}{2}3mv^2 &=& \frac{1}{2}2m v'^2 + \frac{1}{2}3mu'^2 \end{array} \end{split}\]

Now we have 4 unknowns ($v'_x, v'_y, u'_x, u'_y$) but only 3 equations. The outcome seems not to be determined by the initial condition? Of course, that cannot be the case. Think shortly why? The outcome is fully determined by the initial conditions, but we did not set up the equations in the best way because we did not first transform the problem into a 1D problem such that the collision is head-on.

We can use a Galilean Transformation to put one particle at rest. Here we set the blue particle to rest by subtracting $-2vt$. The red particle now has velocity $(-2v,v)$. The problem is still 2D.

\[\begin{split} \begin{array}{rcl} x' &=& x-2vt\\ y' &=& y \end{array} \end{split}\]

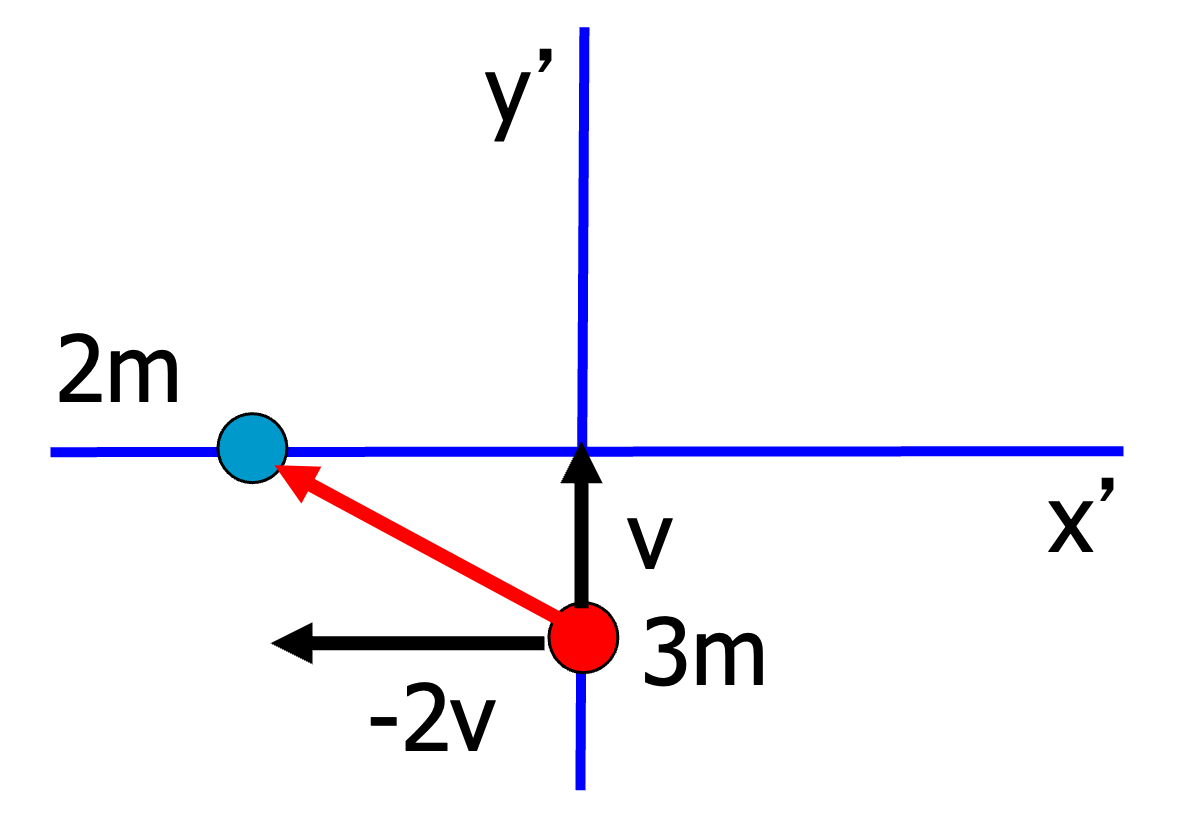
../_images/collisionTrans.png — Fig. 10.4 Applying the Galilean Transformation.#

Next, we can rotate the coordinate system, to obtain a 1D head-on collision that we can solve as above. Later the computed velocities can be converted back to the initial coordinate frame. It is a bit cumbersome, but again conceptually easy.

10.3. Collisions in the Center of Mass frame#

Now let’s consider the CM frame, with the definition of the Center of Mass coordinate as $\vec{R}=\frac{\sum m_i \vec{x}_i}{\sum m_i}$. As the mass is conserved during collision we have 1) $\sum m_i=const$ and as the momentum is conserved $\sum m_i \dot{\vec{x}}_i=const$, we see that the velocity of the CM does not change before and after collision

\[ \dot{\vec{R}}_{before}=\dot{\vec{R}}_{after} \]

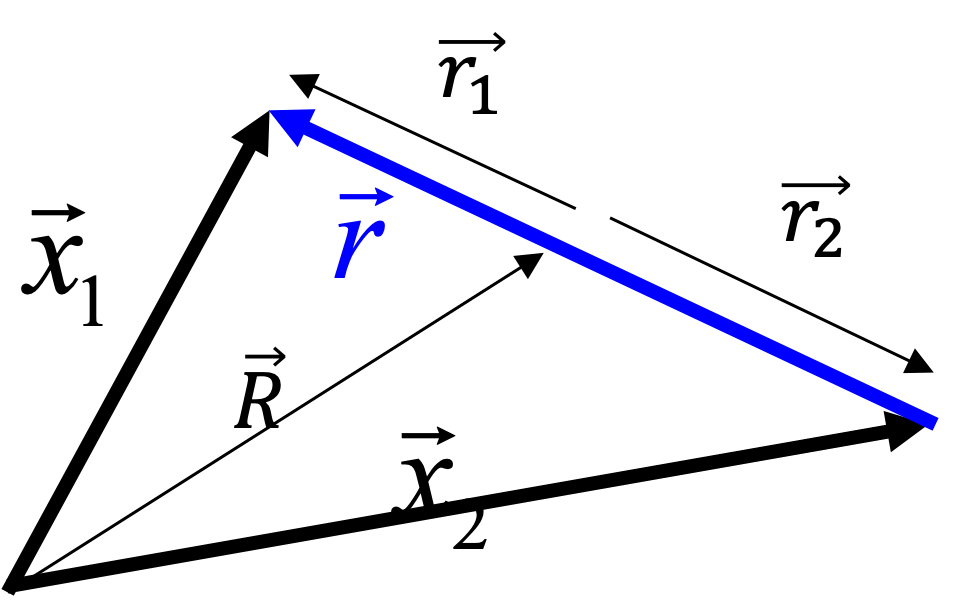
../_images/CMsketch.png — Fig. 10.5 Center of mass.#

For the relative coordinates $\vec{r}_i$ it holds that $\sum m_i \vec{r}_i =0$. Considering 2 particles: The relative distance $\vec{r}=\vec{r}_1-\vec{r}_2 = \vec{x}_1 -\vec{x}_2$ is Galilei invariant.

Using this property together with the reduced mass $\mu$ we obtain expressions for $\vec{r}_1=\frac{\mu}{m_1}\vec{r}$ and $\vec{r}_2=-\frac{\mu}{m_2}\vec{r}$, therefore

\[\begin{split} \begin{array}{lcr} m_1\vec{r}_1 &=& \mu \dot{\vec{r}}_1\\ m_2\vec{r}_2 &=& -\mu \dot{\vec{r}}_2 \end{array} \end{split}\]

This means the momenta of both particles are always equal in magnitude and opposed in direction in the CM frame. Only the orientation of the pair $\dot{\vec{r}}_{1,2}$ can change from before to after the collision.

../_images/CMmomentum.png — Fig. 10.6 Collision in center of mass frame.#

10.4. Inelastic Collisions#

For inelastic collisions only the momentum is conserved, but not the kinetic energy. The total energy is of course always conserved. The kinetic energy after the collision is always less than before the collision. This difference is converted to deformation or heat.

The amount of “inelasticity” or loss of energy can be quantified by the coefficient of restitution $e$

\[ e\equiv \frac{v_{rel,after}}{v_{rel,before}} \]

\[ e^2 \equiv \frac{E_{kin,after}}{E_{kin,before}} \text{ in CM frame} \]

For $e=0$ the collision is fully inelastic, for $e=1$ it is fully elastic. The definition of the coefficient must be independent of the frame of reference therefore relative velocities must be used: $$v_{rel,after} \equiv \| \vec{v}' -\vec{u}' \| \text{ and } v_{rel,before} \equiv \| \vec{v} -\vec{u} \|$$

In the Center of Mass frame, this can als be written as the ratio of the kinetic energy before and after the collision: $E_{kin,rel}=\frac{1}{2}\mu \dot{r}^2$.

10.5. Examples#

10.5.1. Newton’s Cradle#

Click on the image below for a video on Newton’s cradle (gives you also the possibility to ‘play’ with different numerical solvers, from (too) simple to advanced).

10.5.2. Colliding Superballs#

Watch this video on bouncing superballs. We discussed this problem in chapter 7.

Animation

Question

Do you agree with the explanation in the movie?

We seem to violate the conservation of kinetic energy: there is much more kinetic energy after the collision than before! Can you figure out what is happening?

Hint: Look carefully at the bouncing of the blue ball with the earth. Is it really true that the velocity after bouncing is $v$ and that the earth does not move? Probably not, as this violates conservation of momentum!

10.5.3. Elastic Collision#

Click on the image below to start a widget on the elastic collision of two particles.

Or open the widget full screen

10.5.4. Inelastic Collision#

Click on the image below to start a widget on the inelastic collision of two particles.

Or open the widget full screen

10.6. Exercises#

Here are some exercises that deals with oscillations. Make sure you practice IDEA.

Exercise 10.1

A particle of mass $3m$ and velocity $2v$ will collide with a particle of mass $2m$ and velocity $-3v$. The problem is 1-dimensional.

The collision is elastic. Find the velocities of the masses after the collision.
The collision is completely inelastic. Find the velocities of the masses after the collision.
The restitution coefficient is: e=1/5. Find the velocities of the masses after the collision.

Exercise 10.2

A particle of mass $2m$ moves over the x-axis with velocity $v$. It will collide with a particle of mass $m$ that moves over the y-axis also with velocity $v$. The collision is completely inelastic.

Find the velocity of the particles after the collision and calculate the loss of kinetic energy.

Exercise 10.3

A tennis ball is dropped from a height of 1m (with zero initial velocity) on the tennis court. The restitution coefficient is $\frac{1}{2}\sqrt{2}$. After how many bounces does the tennis ball no longer reach a height of 0.25m. Friction with the air can be ignored.

Exercise 10.4

In Hollywood films often one of the persons is shot. That person (whether dead, wounded or ‘just fine’ for the hero) is blown of its feet and may fly a meter or more backwards.

The shooter, however, does not fly or fall backwards.

a) Show that if the victim moves backwards significantly, then the shooter shoot do at least the same. b) A bullet weighs several grams and may have a velocity of several hundred m/s. Estimate what the backward velocity of a victim is. For comparison: when we walk, our velocity is 1 to 2 m/s. Conclusion?

10.6.1. Answers#

Solution to Exercise 10.1

3m has velocity -2v and 2m has velocity 3v
Both particles have zero velocity.
3m has velocity -2/5 v and 2m has velocity 3/5 v.

Solution to Exercise 10.2

\[\vec{v}_{after} = \frac{2}{3}v \hat{x} + \frac{1}{3}v \hat{y}\]

\[\Delta E_{kin} = -\frac{2}{3}mv^2\]

Solution to Exercise 10.3

After each bounce, the tennis ball reaches half of the height it had before the bounce. Thus after two bounces, the ball reaches 25cm and with the third bounce only 12.5cm.

Solution to Exercise 10.4

a) We can consider the shooting as a collision. Bullets don’t bounce back, they penetrate a body. So the victim ‘gains’ maximum momentum if the bullet stays in the body. Then according to conservation of momentum, we have for this inelastic collision:

\[m_b v_b + M_v \cdot 0 = \left ( m_b + M_v \right ) U\]

Thus the velocity of the victim after being shot is:

\[U = \frac{m_b}{m_b + M_v} v_b \]

For the shooter a similar argument holds: before the shot, bullet & shooter have zero momentum. After firing, the bullet has. Thus conservation of momentum requires:

\[0 = m_b v_b + M_s U_s\]

and we find for the velocity of the shooter:

\[U_s = -\frac{m_b}{M_s} v_b\]

Conclusion: as the mass of the bullet is negligible both shooter and victim have similar velocities. As their mass is comparable, it is clear: from a physics point of view, if the victim is blown backward, than also the shooter is.

b) From the above we get, using $m_b \approx 10 \cdot 10^{-3}$kg, $v_b \approx 500$m/s and $M_v \approx 70$kg:

\[U_v = \frac{m_b}{m_b + M_v} v_b \approx 7 cm/s\]

That is much too little to ‘knock’ someone over. Hollywood is good at ‘dramatic effects’, not so good at physics.

10.7. Do it yourself#

Is the restitution coefficient of a bouncing tennis ball a constant or does it depend on the velocity at bouncing? You can ‘easily’ find out yourself. What you need is a tennis ball, a ruler (e.g. from IKEA) and your mobile.

Experiment: drop a tennis ball with zero initial velocity from various height, $H$. Record with the camera of your mobile making sure the ruler is visible in the images. Read out the height before and after the bounce and compute the restitution coefficient $e$. Plot $e$ as a function $H$ and you will have answered the above question.