7. Conservation Laws / Galilean Transformation

In the previous chapters, we have seen that from Newton’s three laws, we can obtain conservation laws. That means, under certain conditions (depending on the law), a specific quantity can not change.
These conservation laws are very important in physics. They tell us that no matter what happens, certain quantities will be present in the same amount: they are conserved.
Conservation of energy follows the concept of work and potential energy. Conservation of momentum is a direct consequence of N2 and N3. And finally, under certain conditions, angular momentum is also conserved. In this chapter we will summarize them. The reason is: their importance in physics. These laws are very general and in dealing with physics questions they give guidance and very strict rules that have to be obeyed. They form the foundation of physics that can not be violated. They provide strong guidance and point at possible directions to look for when analyzing problems in physics.

7.1. Conservation of Momentum

Consider two particles that mutually interact, that is they exert a force on each other. For each particle we can write down N2:

\[\begin{split} \left . \begin{array}{ll} \frac{d\vec{p}_1}{dt} = \vec{F}_{21} \\ \frac{d\vec{p}_2}{dt} = \vec{F}_{12} = - \vec{F}_{21}\end{array} \right \} \rightarrow \frac{d}{dt} \left ( \vec{p}_1 + \vec{p}_2 \right ) = 0 \Rightarrow \vec{p}_1 + \vec{p}_2 = const \end{split}\]

The total (linear) momentum is conserved if only internal forces are present; “action-reaction pairs” always cancel out.
This law has no exception: it must be obeyed all the time. The total momentum is constant, momentum lost by one must be gained by others.

7.2. Conservation of Energy

As we have seen when deriving the concept of potential energy, for a system with conservative forces the total amount of kinetic and potential energy of the system is constant. We can formulate that in a short way as:

\[ \sum{E_{kin}} + \sum{V} = const \]

Again: energy can be redistributed but it can not disappear nor be formed out of nothing.

If non-conservative forces are present, the right hand side of the equation should be replaced by the work done by these forces.

\[ \sum{E_{kin}} + \sum{V} = \sum W \]

In many cases this will lead to heat, a central quantity in thermodynamics and another form of energy. The “loss” of energy goes always to heat. With this ‘generalization’ we have a second law that must always hold. Energy can not be created nor destroyed. All it can do is change its appearance or move from one object to another.

7.3. Conservation of Angular Momentum

Also angular momentum can be conserved. According to its governing law \(\frac{d\vec{l}}{dt} = \vec{r} \times \vec{F}\) it might seem that we can for two interacting particles again invoke N3 “action = -reaction” and the terms with the forces will cancel out. But we need to be a bit more careful, as outer products are involved which are bilinear. So, let’s look at the derivation of “conservation of angular momentum” for two interacting particles:

\[\begin{split} \left . \begin{array}{ll} \frac{d\vec{l}_1}{dt} = \vec{r}_1 \times \vec{F}_{21} \\ \frac{d\vec{l}_2}{dt} = \vec{r}_2 \times \vec{F}_{12} = -\vec{r}_2 \times \vec{F}_{21}\end{array} \right \} \rightarrow \frac{d}{dt} \left ( \vec{l}_1 + \vec{l}_2 \right ) = \left ( \vec{r}_1 -\vec{r}_2 \right ) \times \vec{F}_{21} \end{split}\]

As we see, this is only zero if the vector \(\vec{r}_1 -\vec{r}_2\) is parallel to the interaction forces. This particular case is called central force. Luckily, in many cases the interaction force works over the line connecting the two particles (e.g. gravity). In those cases, the angular momentum is conserved. Mathematically we can write this as:

\[ \text{if } \vec{F}_{21}\, ||\, (\vec{r}_1 -\vec{r}_2)\ \Rightarrow \ \vec{l}_1 + \vec{l}_2 = const \]

7.4. Conservation of Mass

Within the world of Classical Mechanics, mass is also a conserved quantity. Whatever you do, what ever the process, the total mass in the system stays the same. We can not create nor destroy mass. From more modern physics we know that this is not true. On the one hand we can destroy mass. For instance, when an electron and a positron collide, they can annihilate each other resulting in two photons, i.e. ‘light particles’ that do not have mass. Similarly, we can create mass out of light. This is the inverse of the annihilation: pair production. If we have a photon of at least 1.022 MeV (= 1.66 10\(^{-13}\)J), then -under the right conditions- an electron-positron pair can be created.

Moreover, Albert Einstein showed that mass and energy are equivalent - expressed via his famous equation \(E = mc^2\). His theory of Relativity showed us that in collisions at extreme velocities mass is not conserved: it can both be created or disappear. Rephrased: it is actually part of the energy conservation, mass is in that context just a form of energy.

Emmy Noether, symmetries and conservation laws

We discussed the conservation laws as consequences of Newton’s Laws. That in itself is ok. However, there is a deeper understanding of nature that leads to these conservation laws. And from the conservation laws we can go to Newton’s Laws, thus ‘reversing the derivations’ and starting from this new, different way of looking at nature.

What is it and how do we know? To answer this question we have to resort to Emmy Noether, a German mathematician. Noether made top contributions to abstract algebra. She proved, what we now call, Noether’s first and second theorems, which are fundamental in mathematical physics. Noether is often named as one of the best if not the best female mathematicians ever lived. Her work on differential invariants in the calculus of variations has been called “one of the most important mathematical theorems ever proved in guiding the development of modern physics”.

Fig. 7.1 Amalie Emmy Noether (1882-1935). From Wikimedia Commons, public domain.

Noether shows, that if a dynamic system is invariant under a certain transformation, that is it has a symmetry, then there is a corresponding quantity that is conserved. Ok, pretty abstract. What does it mean, any examples? Yes! Here is one.

In physics we believe that it does not matter if we do an experiment now and repeated it exactly under the same conditions an hour later, the outcome will be the same. Or rephrased: if we translate it in time, the outcome is the same; the laws of physics are invariant. This is in mathematical terms a symmetry, a symmetry with respect to time. Noether’s theorem then shows, that there is a conserved quantity and this quantity is energy. Hence, based on the idea that time itself has no effect on physical laws, we immediately arrive at conservation of energy.

Second example: we also believe that place or position in the universe doesn’t matter. The physicals laws are not only always the same (time invariance), they are also the same everywhere (space invariance). From this symmetry, via Noether’s work, we immediately get that momentum is a conserved quantity. Thus, these two invariances or symmetries -time and space - provide us directly with conservation of energy and momentum and from that we could easily derive Newton’s second and third law. Much of modern physics is now build on the ideas put forward by Emmy Noether. That goes from quantum mechanics to quarks to string theory.

7.5. Galilean Transformation

There is one important element of Classical Mechanics that we have to add: for which type of observer do Newton’s Laws hold? The original thought was: for inertial observers. These are observers that are at rest with respect to an inertial frame of reference.

But this merely shifts the question to: what is an inertial frame of reference. One possible answer is: an inertial frame of reference is a frame in which Newton’s Laws hold. That is: a particle on which, according to an observer in such a frame, no net force is acting will keep moving at a constant velocity.

All inertial frames of reference move at a constant velocity with respect to each other. They can not accelerated. To picture what it means, an inertial frame of reference or an inertial observer, we sometimes use the idea that such a frame or observer moves at a constant velocity with respect to the fixed stars. And indeed, for a long time people believed that the stars were fixed in space. But from more modern times we do know, that this is not the case: stars are not fixed in space nor do they move at a constant velocity.

Later on, we will see, that it is possible to do without the restriction that Newton’s Law strictly speaking only hold in inertial frames. But first we will look into inertial frames and the ‘communication’ between two observers in two different frames. An important requirement of any physical law is that it looks the same for all inertial observers. That doesn’t mean that the outcome of using such a law is the same. As a trivial example, take two inertial observers S and S’. According to S, S’ moves at a constant velocity, \(V\), in the \(x\)-direction. S’ observes a mass \(m\) that is not moving in the frame of reference of S’. For simplicity, we will assume that each observer is in its own origin. S’ rightfully concludes, based on Newton’s 1\(^{st}\) law that no force is acting on \(m\). S agrees, but doesn’t conclude that \(m\) is at rest. This is trival: both observers can use Netwon’s second law which for this case states that \(\frac{d\vec{p}}{dt} =0 \rightarrow \vec{p} = const \rightarrow \vec{v} = const\). But the constant is not the same in both frames.

To make the above loose statements more precise. We have two coordinates systems CS and CS’. The transformation between both is given by a translation of the origin \(\vec{R}\) and a rotation given by the rotation matrix \(D\) (in 2D or 3D) in the form

\[ \vec{x}' = D\, (\vec{x}-\vec{R}) \]

Now the statement: Newton’s equation of motion \(\vec{F}=m\vec{a}\) have the same form in CS and CS’ can be formulated as the requirement on the transformation \(\dot{D} =0\) and \(\ddot{\vec{R}}=0\), i.e. the rotation is time independent and the origin offset must not accelerate.

In the case \(\dot{D}\neq 0\) or \(\ddot{\vec{R}}\neq 0\) Newton’s equation of motion obtain additional terms (called fictitious or inertial forces). We will treat these cases later in the chapter on non-inertial systems.

We assume that a CS without inertial forces exist, and such a system we call inertial system. I.e. we can write down Newton’s equation in the form of \(\vec{F}=m\vec{a}\). If one CS is an inertial system, then CS’ is also a inertial system if they are linked by a coordinate transformation \(\vec{x}' = D\, (\vec{x}-\vec{R})\) with \(\dot{D}=0\) and \(\ddot{\vec{R}}=0\). The transformation that fulfills such a change is called the Galilean Transformation.

7.6. Communication Protocol

The transformation between inertial frames may only contain a constant velocity (by \(\ddot{\vec{R}}=0\)). In addition the frames must not rotate with respect to each other as a function of time (\(\dot{D}=0\)). As a consequence, velocities, as observed by two different inertial observers, differ by a fixed, constant velocity, whereas accelerations are the same for both observers.

This can easily be seen by the basic Galilean Transformation between two inertial frames, \(S\) and \(S'\). According to observer \(S\), \(S'\) is moving at a constant velocity \(V\). Both observers have chosen their coordinate system such that \(x\) and \(x'\) are parallel (we ignore the possibility of the rotational shift for simplicity in all the discussion and assume \(D\) as the identity matrix, that is: S and S’ are not rotated with respect to each other). Moreover, at \(t=t'=0\), the origins \(O\) and \(O'\) coincide. The picture below illustrates this.

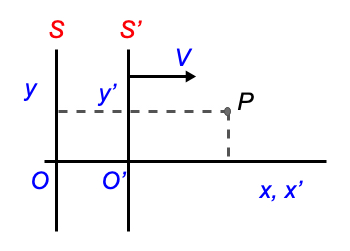
Fig. 7.2 Two inertial observers S and S’ and their coordinate systems.

Consider for simplicity a 2D point \(P\) with coordinates \((x',y')\) and time \(t'\) for \(S'\). What are the coordinates according to \(S\)? First of all: in classical mechanics, there is only one time, that is: \(t=t'\). Until the days of Einstein this seemed self evident; we now know that nature is more complex.

For the spatial coordinates, we see immediately: \(y=y'\). And for the \(x\)-coordinate \(S\) can do the following. To go to the \(x\)-coordinate of \(P\), first \(S\) goes to the origin \(O'\) of \(S'\). \(O'\) is a distance \(Vt\) from \(O\). Thus, the distance to \(P\) along the \(x\)-axis is \(Vt+x'\). If we sum the above up, we can formulate the relation between the coordinate system of the two observers. This transformation is known as Galilean Transformation, GT for short.

Galilean Transformation

\[\begin{split} \begin{split} x' &= x - Vt \\ y' &= y \\ t' &= t \end{split} \end{split}\]

7.6.1. Velocity is relative; acceleration is absolute

A direct consequence of the Galilean Transformation is that velocity is observer-dependent (not surprising), but for observers in inertial frames, observed velocities differ by a constant velocity vector.

In what follows we will derive the relations between velocity as well as acceleration as observed by S and S’. Note that we need to be precise in our notation: S denotes quantities without a prime (‘), but S’ does. This is obvious for the coordinates as S uses \(x\) whereas S’ will write \(x'\). It is, however, also wise to use primes on the velocity: S will denote the \(x\)-component as: \(v_x = \frac{dx}{dt}\). So, S’ will note denote velocity by \(v\), but by \(v'\). Hence S’ will write \(v'_{x'} = \frac{dx'}{dt'}\). Now, obviously, \(t'=t\) so we could drop the prime on time, but it is handy to do that in the second step.

First we look at velocity.

\[\begin{split} \begin{split} v'_{x'} &\equiv \frac{dx'}{dt'} \Rightarrow v'_{x'} = \frac{d(x-Vt)}{dt} = v_x - V\\ v'_{y'} &\equiv \frac{dy'}{dt'} \Rightarrow v'_{y'} = \frac{dy}{dt} = v_y \end{split} \end{split}\]

Thus indeed velocity is ‘relative’: different observers find different values, but they do have a simple protocol to convert information from the other colleague to their own frame of reference.

Secondly, we look at acceleration.

\[\begin{split} \begin{split} a'_{x'} &\equiv \frac{dv'_{x'}}{dt'} \Rightarrow a'_{x'} = \frac{d(v_x-V)}{dt} = a_x\\ a'_{y'} &\equiv \frac{dv'_{y'}}{dt'} \Rightarrow a'_{y'} = \frac{dv_y}{dt} = a_y \end{split} \end{split}\]

So, we conclude: acceleration is the same for both observers.

Consequently, N2 holds in both inertial systems if we postulate that \(m' = m\). In other words: mass is an object property that does not depend on the observer.

Thus, two observers, each with its own inertial frame of reference, will both see the same forces: \(\vec{F} = m\vec{a} = m'\vec{a}' = \vec{F}'\).

This finding is stated as: Newton’s second law is invariant under Galilean Transformation. Invariant means that the form of the equation does not change if you apply the Galilean coordinate transformation. Later we will expand this to Lorentz invariant transformation in the context of special relativity. The concepts of invariance is very important in physics as hereby we can formulate laws that are the same for everybody (loosely speaking).

7.7. Navier-Stokes and Galileo invariance

In what follows, we look at an example of the consequences of GT.

In hydrodynamics the conservation of mass in a fluid or gas is described in 1D by

\[ \frac{\partial \rho }{\partial t} + \frac{\partial (\rho v)}{\partial x}=0 \]

with \(\rho(x,t)\) the mass density (unit kg/m\(^{3}\)) and \(v(x,t)\) the flow velocity field. This continuity equation was introduced by Claude Navier and George Stokes around 1840 and it is Galileo invariant.

You can visualize the statement of the equation and derivation as follows. In a liquid (but also for gasses) the mass that flows into a volume element and out of it is conserved. Through an area \(A\) perpendicular to the flow direction the inflow of mass into a small element of length \(dx\) is \(\rho A vdt|_{x}\) and the out flow is \(\rho Avdt|_{x+dx}\). As the mass is conserved we have \(M(t+dt)-M(t) = \rho A v|_{x}dt - \rho Av|_{x+dx}dt\). Now we replace \(M(t)=\rho Adx\) and can rearrange to find the continuity Navier-Stokes equation.

Intermezzo Continuity Equation

You will find these type of “conservation equations” for different kind of phenomena later in your study, they are called continuity equations. A certain property, here mass, is continuous and its change in time must be compensated by in or out flow of the same quantity. The general form of the equation is

\[ \frac{\partial \rho}{\partial t}+div\ \vec{j} = 0 \]

Where the divergence is the inner product of the nabla operator with the vector field \(\nabla \cdot \vec{j}(\vec{x},t)\) and \(\vec{j}\) represents the flux of the quantity. You will see continuity equations again as conservation of charge in Electromagnetism, as heat transfer in Thermodynamics, in semi-conductors (for electron and holes) in Solid State and even in Computer Vision as Optic Flow.

We will now show that the continuity equation is GT invariant. We use the formalism of transformation again later for Maxwell’s equations when going to the special theory of relativity.

For an observer \(S'\) with coordinates \(x'=x-Vt, t'=t\) the equation needs to be transformed, i.e. the partial derivatives. The density \(\rho( x(x',t'), t(x',t'))\) is a function of two variables \(x',t'\). The chain rule gives us in general

\[\frac{\partial f(x(x',t'))}{\partial x} = \frac{\partial f}{\partial x'}\frac{\partial x'}{\partial x} + \frac{\partial f}{\partial t'}\frac{\partial t'}{\partial t}\]

and thus for the space derivative

\[ \frac{\partial}{\partial x}= \frac{\partial}{\partial x'}\frac{\partial x'}{\partial x} + \frac{\partial}{\partial t'}\frac{\partial t'}{\partial x} \]

Luckily the GT is simple and the derivatives simply \(\frac{\partial x'}{\partial x}=1\) and \(\frac{\partial t'}{\partial x}=0\). Therefore we have

\[ \frac{\partial}{\partial x}=\frac{\partial}{\partial x'} \]

For the time derivate we find

\[ \frac{\partial}{\partial t}= \frac{\partial}{\partial t'}\frac{\partial t'}{\partial t} + \frac{\partial}{\partial x'}\frac{\partial x'}{\partial t} \]

with \(\frac{\partial t'}{\partial t}=1\) and \(\frac{\partial x'}{\partial t}=-V\) we have

\[ \frac{\partial}{\partial t}= \frac{\partial}{\partial t'}-V \frac{\partial}{\partial x'} \]

Combining the above for the transformed equation in \(x',t'\)

\[ \frac{\partial \rho }{\partial t'} -V\frac{\partial \rho }{\partial x'} + \frac{\partial (\rho v)}{\partial x'} = 0 \]

If we now realize that \(v'\equiv v-V\), and recall \(V=const\), then the equation reads

\[ \frac{\partial \rho }{\partial t'} + \frac{\partial (\rho v')}{\partial x'}=0 \]

therefore also an observer in \(S'\), with \(\rho' (x',t')=\rho (x,t)\), can write the Navier-Stokes equation as

\[ \frac{\partial \rho' }{\partial t'} + \frac{\partial (\rho' v')}{\partial x'}=0 \]

in his own coordinates such that the form of the equation is preserved between \(S\) and \(S'\).

If we cannot find a \(\rho'\) and \(v'\) such that the equations have the same form, the Navier-Stokes equations would not have been Galilei invariant (which is bad of course as all relevant physical laws must be invariant under this coordinate transformation).

7.8. Worked Example

In class you have seen the Superballs example. You can watch it here again. The explanation is not really correct there, we will reason the observations here.

If you let a smaller and a larger ball drop together, stacked on top of each other, the smaller ball will bounce back much stronger (higher) than if you let the small ball fall without stacking it on the lager ball. How can that happen?

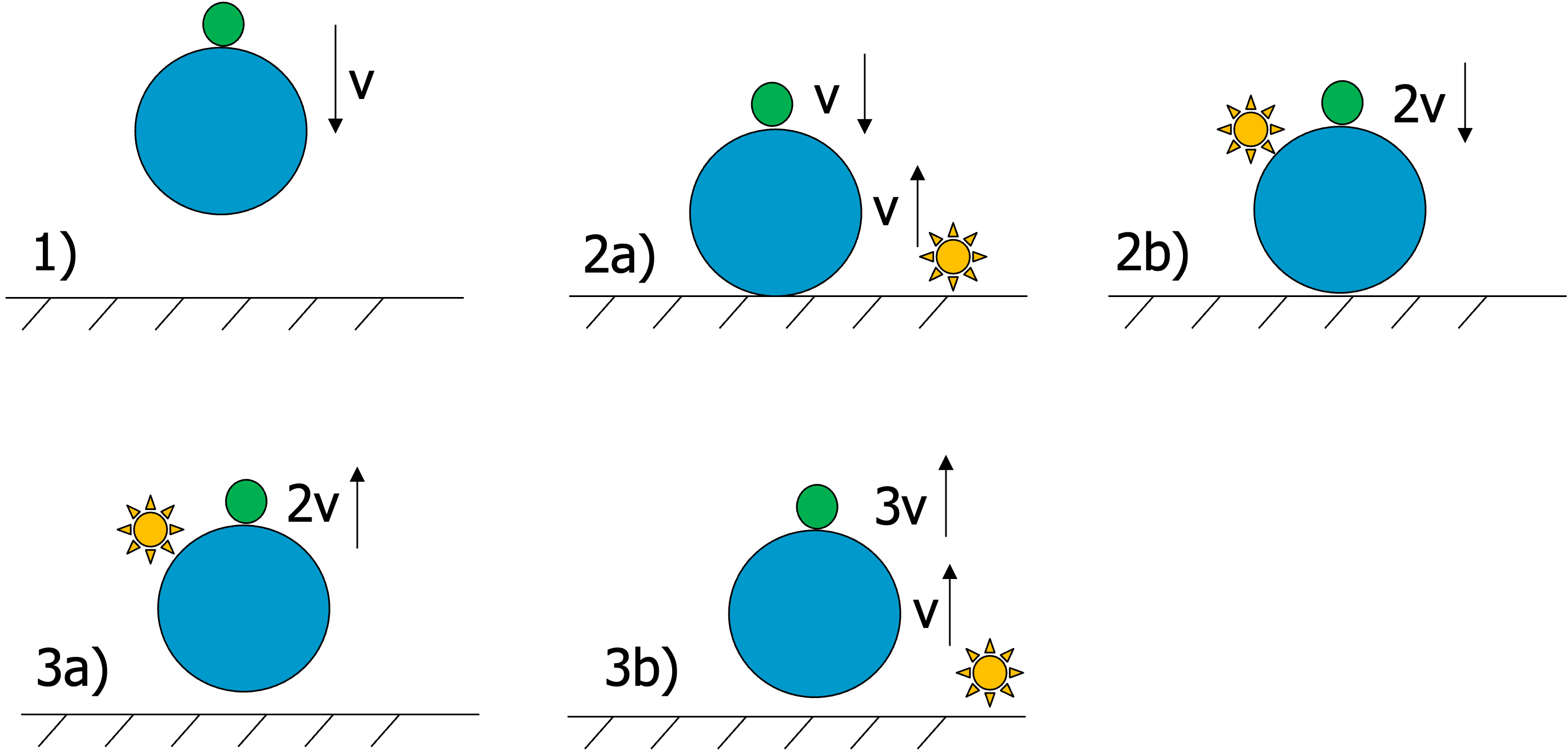
Fig. 7.3 Bouncing balls.

To explain this we use the Galilean Transformation (GT).

• Situation 1). Both balls are falling with velocity \(\vec{v}\) towards the ground.

• Situation 2a). The larger ball just hit the ground. As the mass of the ground is much larger than that of the large ball, it is (elastically) reflected, i.e. the direction of the velocity is reversed but the magnitude stays the same. The small ball is still moving downwards with \(\vec{v}\).

• Situation 2b). We apply a GT of the observer (yellow star) from the ground to an observer moving with the larger ball. The observer moving with the larger ball sees the smaller ball moving with \(2\vec{v}\) towards it.

• Situation 3a). The smaller ball hits the larger ball and is reflected due to its smaller mass. In the frame of the observer on the larger ball, the smaller ball now moves with \(2\vec{v}\) away from it.

• Situation 3b). We apply a GT of the observer (yellow star) from the larger ball back to an observer on the ground. For the observer on the ground the larger ball has velocity \(\vec{v}\) upwards from 2a), therefore the smaller ball has velocity \(3\vec{v}\) upwards.

The smaller ball has now velocity \(3\vec{v}\) instead of \(\vec{v}\) if you drop it without the larger ball. NB: If you would use three balls instead of two, the third ball would have a velocity of \(7\vec{v}\) using the same reasoning as above.

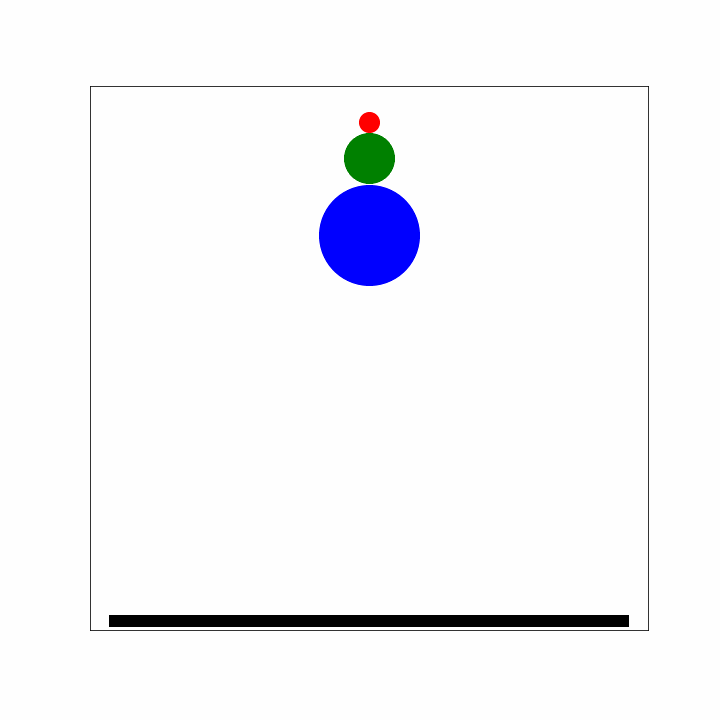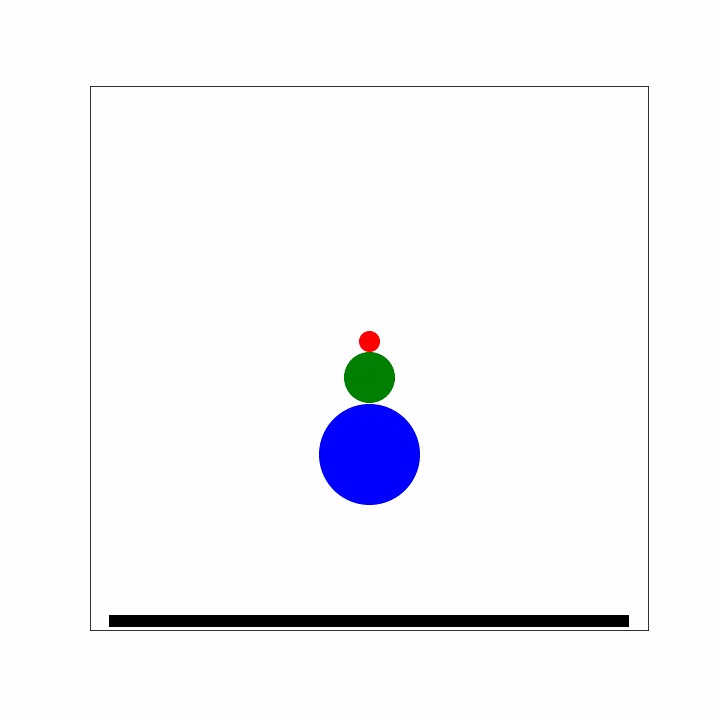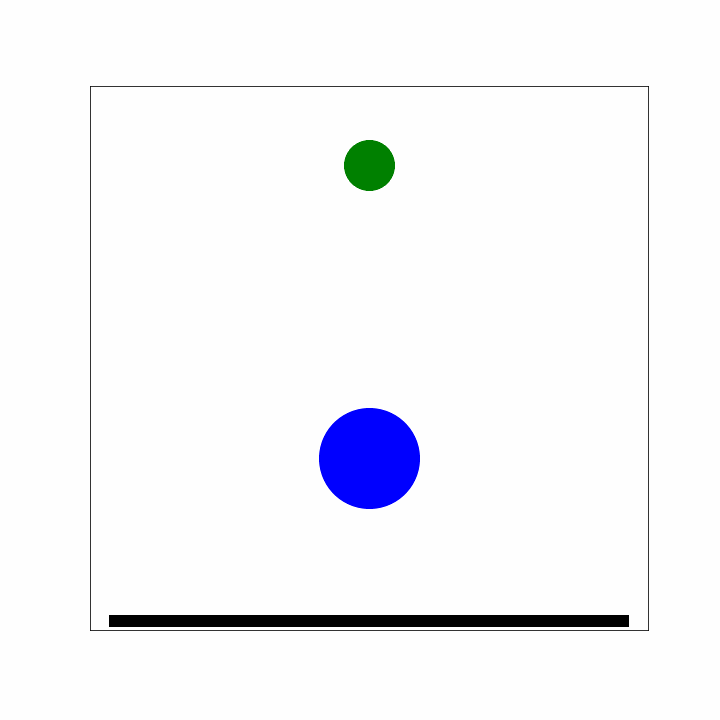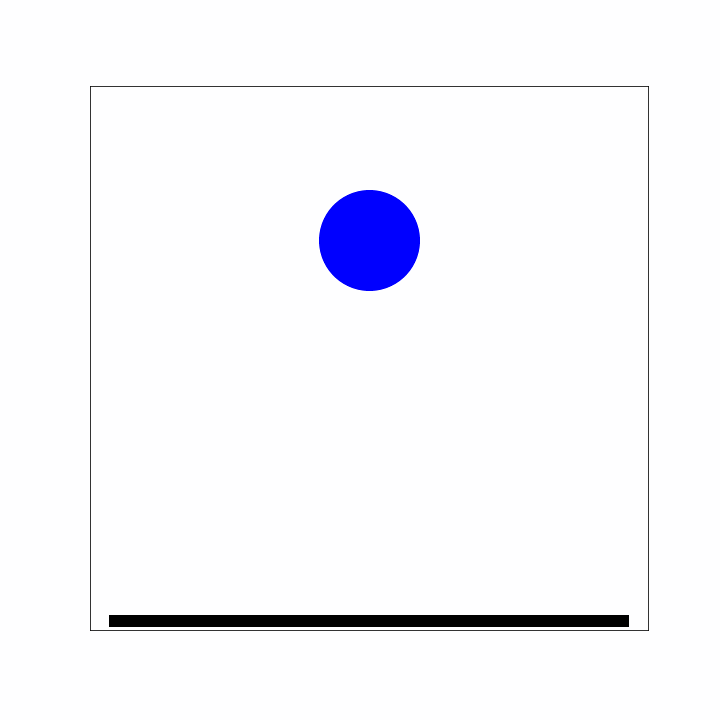
Fig. 7.4 Bouncing of three (super)balls.

How much higher does the smaller ball fly with velocity \(3\vec{v}\) compared to \(\vec{v}\)?

Answer
We equate the kinetic energy when the ball is just reflected with the potential energy when the ball reached it maximal height before falling back.

\[ \frac{1}{2}mv^2 = mgh \Rightarrow h = \frac{v^2}{2g} \]

Therefore the ball with \(3v\) flies 9 times higher.

What is very fishy about this whole outcome?
In situation 1) the kinetic energy is \(\frac{1}{2}m_s v^2 + \frac{1}{2}m_\ell v^2\), but in situation 3b) it is \(\frac{1}{2}m_s (3v)^2 + \frac{1}{2}m_\ell v^2\) while the potential energy is zero in both cases. This clearly does not add up! But energy must be conserved under all circumstances!

The conclusion is, that we did make an approximation and did not solve the energy and impulse conservation equations for elastic collisions. Even for the case \(M \gg m\) there is some momentum transfer. If you solve for the velocity of \(m\) after the collision with \(M\), you obtain

\[ v' = \frac{\frac{m}{M}-1}{\frac{m}{M}+1} v \]

For \(M \gg m\) you indeed see \(v'=-v\). Thus the smaller ball will have a smaller velocity than reasoned above and the larger ball with also have a smaller velocity (in the experiment you can clearly notice that it does not fly as high as when it drops without the small ball on top). In real life, the balls also deform which makes the collision inelastic.

7.9. Examples

Example 7.1

Consider yourself biking at a constant velocity on an unlikely day with zero wind. Still, you experience a frictional force from the air, with the following observation: the faster you bike, the larger this force. An experimentalist is trying to measure the friction force of the air and relate it to your velocity. She finds that, by and large, this force turns out to scale with the square of your velocity \(v_b\)

\[ F_f \propto v_b^2 \]

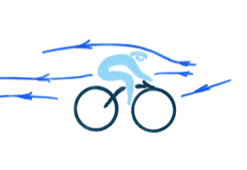
Fig. 7.5 Air resistance on cyclist.

Understanding the Galilean transformation, you immediately see that this can’t be correct. In your frame of reference, your velocity is zero. And thus, the friction force would be zero. But that cannot be true: both observers should see the same forces. What you see, is that the air is blowing at a speed \(v_{air}−v_b\) past you. And indeed, the faster you bike, according to the experimentalist, the faster you see the air moving past you: velocity is relative.

You quickly realize that a proper description of the air friction must depend on the relative velocity between you and the air. relative velocities are invariant under Galilean transformation:

\[ F_f \propto (v_b - v_{air} )^2 \]

Example 7.2

Riding a bike while it rains. You have done this 100s of times. Your front gets soaked, while the backside of your coat stays dry. Or if you have a passenger on your carrier he/she will not get wet, while you take all the water. From a GT to the reference frame of the biker it is obvious why this is the case. The rain is not falling straight from the sky, but at an angle towards him.

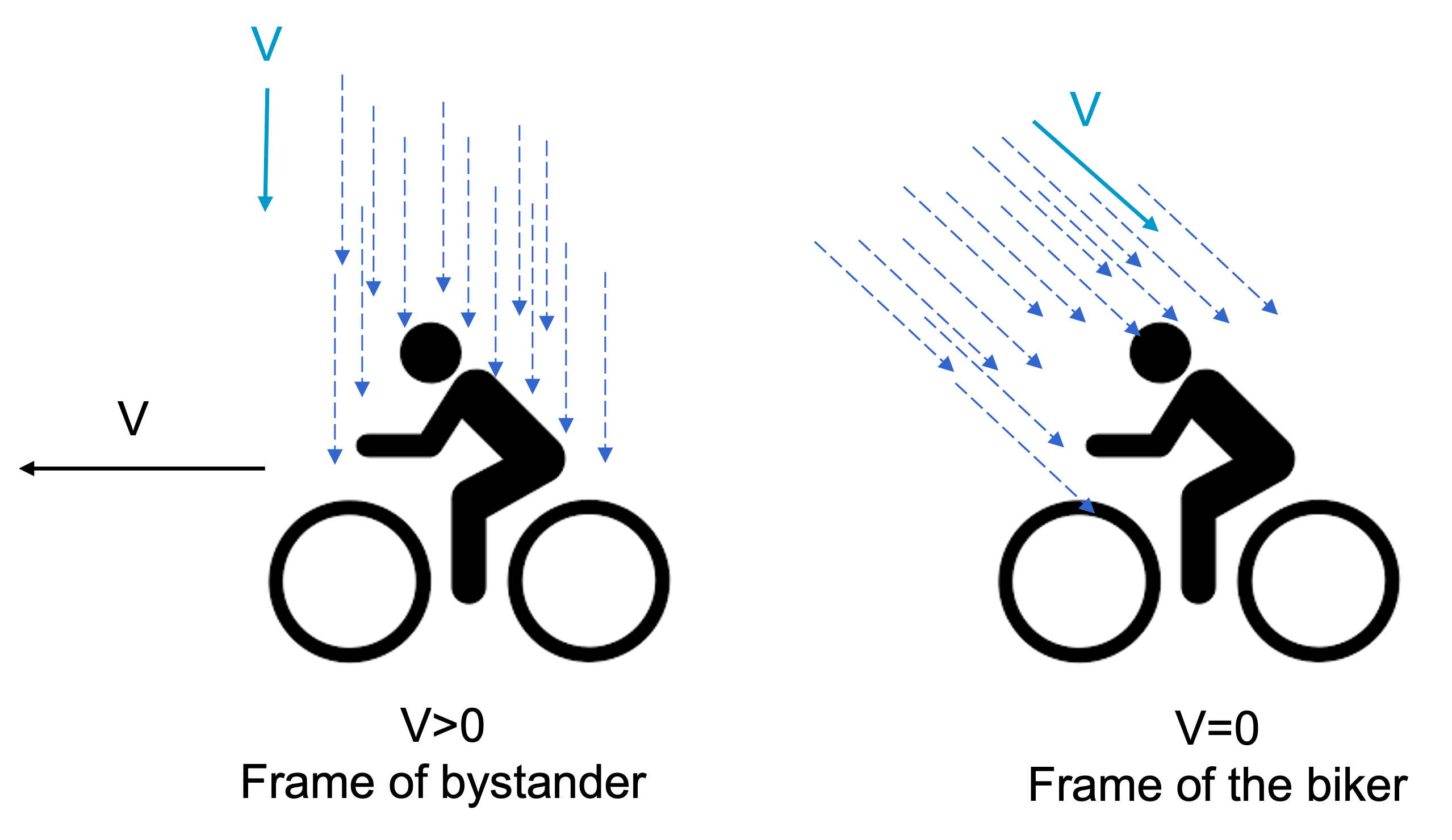
Fig. 7.6 Riding a bike in the rain.

NB: For Dutch bikers you have had this experiences with head wind and rain all your life.

7.10. Demo

A ball is bouncing at a wall. The mass of the wall is much greater than that of the ball. So, acceleration of the wall can be ignored.

On the left side, we see this from the perspective of an observer, S, standing next to the wall. The right side shows what observer S’ sees, who is traveling with the ball as it moves towards the wall. Notice, that both S and S’ are inertial observers. That is, they keep their velocity and are no part of the collision. What would Galilei say?

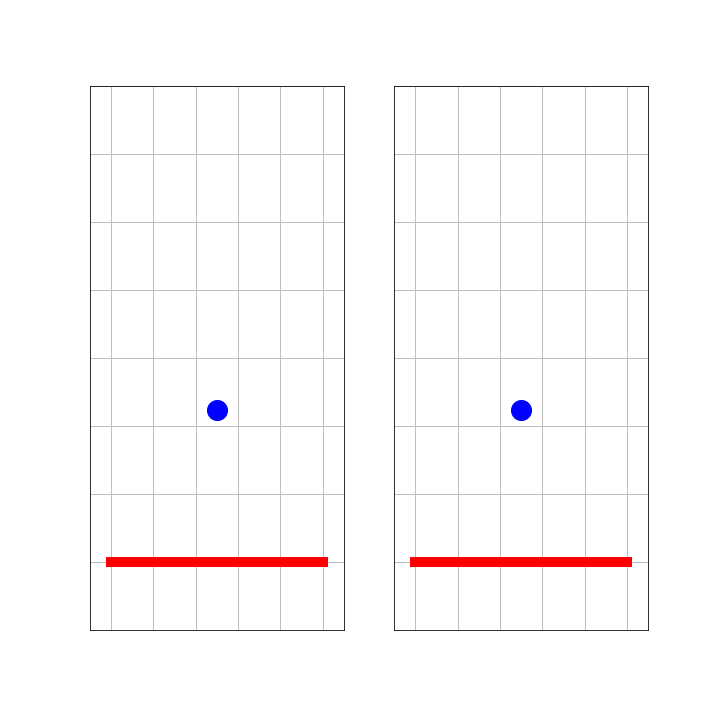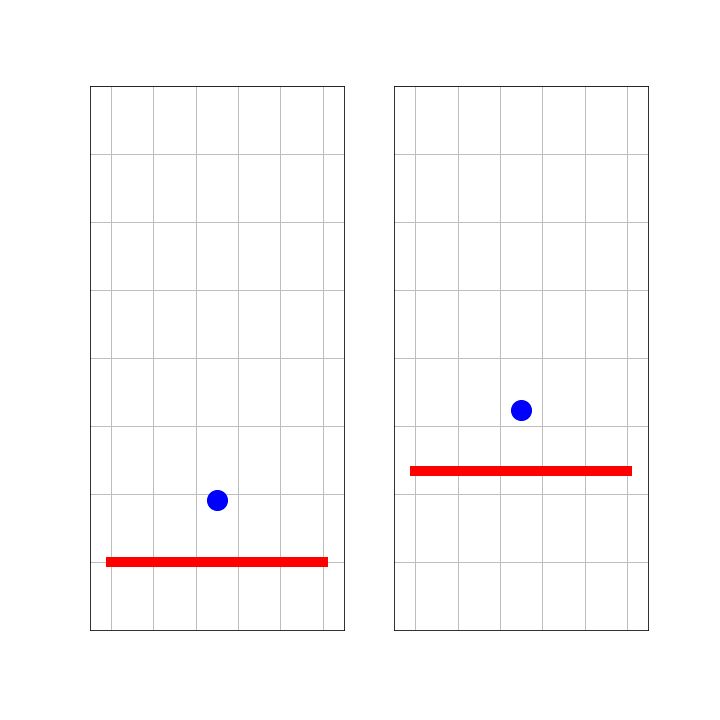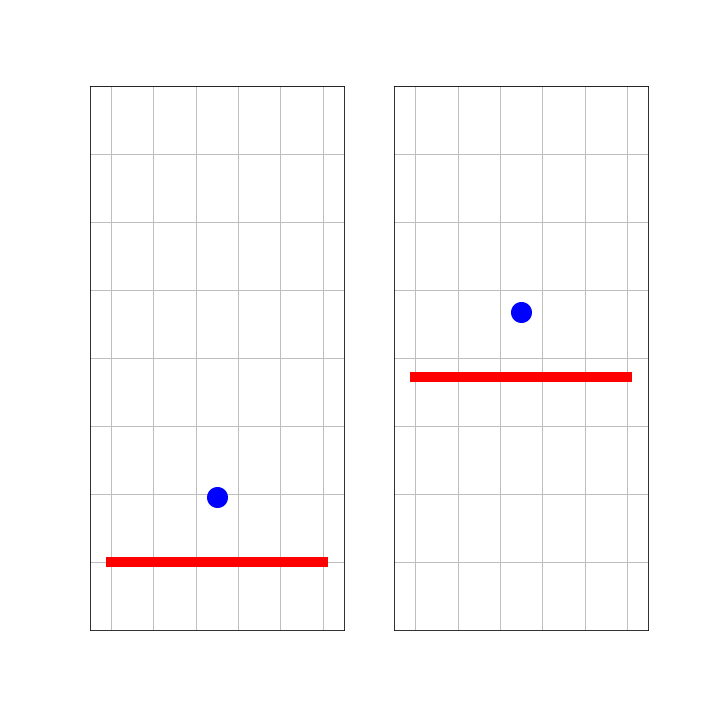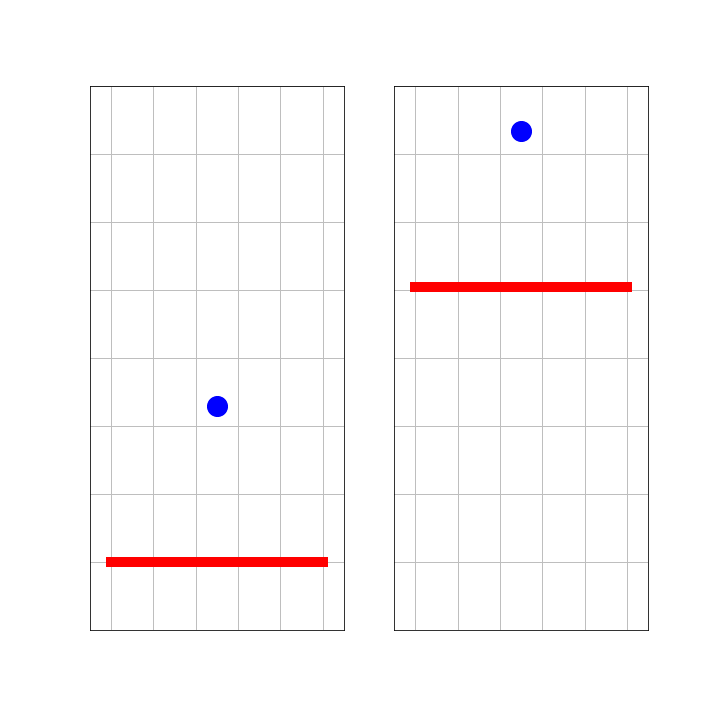
Fig. 7.7 Ball bouncing at a wall.

7.11. Exercise

Exercise 7.1

A train is passing a station at a constant velocity \(V\). At the platform that the train passes, an observer \(S\) sees that in the middle of the train (train length \(2L\)), at \(t=0\) an object is released with a constant velocity \(u\). The object moves towards the back of the train and, at some point in time, will hit the back.

Inside the train, observer \(S'\) sees the same phenomenon. Show that both find the same time for the object hitting the back of the train. Ignore the effect of gravity.

Exercise 7.2

Show that the equation of motion \(\dot{\vec{p}}=\vec{F}\) is invariant under rotation of the coordinate system, i.e. the orientation of the axes in the inertial frame do not matter.

Exercise 7.3

Observer \(S'\) (coordinate system \(x’,y’,z’\)) moves with constant velocity V with respect to observer \(S\) (coordinate system \(x,y,z\)). The \(x\) and \(x’\)-axes are parallel and taken such that V is parallel to them. At time \(t=0\) the origin \(O’\) of \(S’\) coincides with the origin \(O\) of \(S\).
\(S\) observes a mass \(m\) moving over the \(x\)-axis with at \(t=0\) velocity \(V/2\). At time \(t=0\), \(m\) is in \(O\). \(m\) is accelerating at a constant acceleration \(a\). According to \(S\), there is an obstacle at \((x_w,0,0)\), with which \(m\) will collide.

Show that the collision takes place at the same time for \(S\) and \(S'\).

7.11.1. Answers

Solution to

In fig:Ex71.svg the situation is sketched. Please note, that we have drawn information as seen by \(S\) and by \(S'\) in the same figure. For instance: the velocity of the train is denoted by \(V\), that is without a prime. This is the velocity of the train according to \(S\). Observer \(S'\) would, of course, say that the velocity of the train is zero: \(V'=0\).
Similarly, the velocity of the object is in the figure given as \(u'\), pointing in the negative \(x, x'\)-direction. That is the velocity of the object according to \(S'\). We can plot the velocity of the object as seen by \(S\). However, we do not know if the object, according to \(S\), is moving to the left or to the right. That obviously depends on the magnitude of \(V\) and \(u'\). It is straightforward to figure out what\(S\) will see: velocity is relative, i.e. using GT we have for any velocity in the \(x, x'\)-direction:

\[ v' = v - V\]

Thus, if according to \(S\) the object is moving in the negative \(x,x'\)-direction the magnitude of \(u'\) is larger than that of \(V\). If, according to \(S\) the object is not moving, then \(u'=-V \lt 0\). And if, according to \(S\) the object moves to the right \(u' \gt -V\) but may still be negative.

According to \(S'\) the object moves at constant velocity \(u' \lt 0\) over the $x’4-axis. Its trajectory is:

\[x_o'(t) = u' t \text{ with } u' \lt 0\]

The object will hit the back wall of the train when:

\[x_o'(T) = -L \rightarrow T= \frac{L}{-u'}\]

According to \(S\), the object has velocity \(u = u' + V\). It may be moving to the left but also to the right. Furthermore, according to \(S\), the back of the train is moving with velocity \(V\). Thus \(S\) describes the situation via:

\[\begin{split}\begin{split} x_o(t) & = ut \\ x_b(t) &= -L +Vt \end{split}\end{split}\]

and will conclude that the object hits the wall at

\[x_o(\tau) = x_b(\tau) \rightarrow \tau = \frac{L}{V-u}\]

\(S\) and \(S'\) use Gt to communicate. Hence, they both can use \(u'=u-V\). When substituting this relation we find:

\[\tau = \frac{L}{V-u} = \frac{L}{-u'} =T \]

Solution to

Consider two inertial observers, \(S\) and \(S'\). \(S'\) uses a coordinate system that is rotated with respect to that of \(S\), but otherwise ‘steady’. We can write the relation between the two coordinates via a rotation matrix \(R\):

\[\vec{r}' = R\vec{r}\]

As the rotation is steady, i.e. not a function of time (it is a ‘one-time rotation’), we easily find the relation for the velocities of both observers:

\[\vec{v}" \equiv \frac{d\vec{r}'}{dt} = \frac{dR\vec{r}}{dt}= \underbrace{\frac{dR}{dt}}_{=0} \vec{r} + R\frac{d\vec{r}}{dt} =R\vec{v} \]

Since the mass, \(m\) of an object is an invariant, we also have:

\[\vec{p}' = R\vec{p}\]

If we now take the time derivative of the momentum as used by \(S'\) we get:

\[\frac{d\vec{p}'}{dt} = \frac{dR\vec{p}}{dt}= \underbrace{\frac{dR}{dt}}_{=0} \vec{p} + R\frac{d\vec{p}}{dt} = R\frac{d\vec{p}}{dt}\]

Using Newton’s second law, we find:

\[ \frac{d\vec{p}'}{dt} = R\frac{d\vec{p}}{dt} = R\vec{F}\]

However, \(R\vec{F} = \vec{F}'\) as every vector gets rotated. Thus:

\[\frac{d\vec{p}'}{dt} = \vec{F}'\]

And we see that N2 has the same form in \(S\) and \(S'\).

Solution to

We start with a sketch.

Observer \(S\) sees the mass \(m\) moving with velocity \(V/2\) at \(t=0\). The acceleration is constant and equal to \(a\). Thus, the trajectory of \(m\) according to \(S\) is:

\[x(t) = \frac{1}{2}Vt + \frac{1}{2}at^2 \]

The collision will take place at \(t=T\):

\[x(T) = x_w \rightarrow \frac{1}{2}Vt + \frac{1}{2}at^2 = x_w \rightarrow T = \frac{\sqrt{V^2+8ax_w}-V}{2a}\]

where we have used that \(T>0\).

\(S'\) will describe this as follows.

\[\begin{split}\begin{split} x'(t) &= -\frac{1}{2}Vt + \frac{1}{2}at^2 \\ x_w'(t) &= x_w - Vt \end{split}\end{split}\]

The collision will take place at:

\[x'(T') = x_w'(T') \rightarrow -\frac{1}{2}VT' + \frac{1}{2}aT'^2 =x_w -VT'\rightarrow \frac{1}{2}VT' + \frac{1}{2}aT'^2 = x_w\]

And this has obviously the same solution.