8. Rutherford & the atom

8.1. Atomic theory

The idea that matter is made of atoms is old. However, the notion of atoms as we have now is relatively young.

In the ancient Greek world, it was as early as the fifth century B.C. that Leucippus and later one of his pupil Democritus proposed that the world, i.e. matter, is made up of tiny, indivisible particles -which he called atoms, derived from the Greek word ‘atomos’, which means uncuttable. These particles float in a vacuum, that was called void by Democritus. We currently have a view that is remarkably close, but at the same time quite different from these first ideas.

In ancient India even earlier (records go back to the eighth’ century B.C.) philosophers like Uddalaka Aruni talk about matter being made up of tiny particles. They did not use terms like atoms, but instead referred to the ‘building blocks’ of matter as ‘kana’ which means particles. In the Islamic world, atomic theories were developed in e.g. the Asharite school by Al Ghazali (1058-1111). In his thinking, atoms are the only material things that live forever. Everything else, any event or interaction is due to God’s intervention.

Although these early thoughts point at atoms as the underlying elements of matter and as such resemble our current understanding of matter, they also differ quite a bit. The early ideas are based on philosophy and the notion that matter is either a continuum that can always be cut in smaller parts that still maintain all characteristics of the original material or that at some point a further splitting in smaller pieces is no longer possible without at least losing some of the characteristics.

In more recent history, the notion of atoms as elementary building blocks is guided by experiments. The English physicist and chemist John Dalton (1766-1844) did ground braking work. For instance, he noticed that water, when decomposed, always resulted in the same elements: hydrogen and oxygen. Moreover, the relative weights of these two was always the same. Furthermore, he came to the conclusion that there is a uniques atom for each element. More chemists noted that many substances were made of the elements in very specific ratio’s. In our modern view we would say: water is formed in a 1 to 2 ratio of oxygen and hydrogen, never in 1 to 2.1 or any other non-integer number.

Although the evidence from chemistry was clear, the notion of atoms as the building blocks remained controversial. One generally accepted the laws of definite proportion (e.g. water is decomposed in a fixed ratio in hydrogen and oxygen), but the hypothesis that everything was made of atoms was not. As a consequence, the work of Ludwig Boltzmann (1844-1906) on statistical thermodynamics that is entirely based on an atomic (or molecular) view was not accepted during Boltzmann’s life.

In the second half of the nineteenth century William Thomson (1824-1907) -later Lord Kelvin- proposed the so-called vortex theory of the atom. Based on the discoveries by chemists of only a few different atoms that made up the rest of matter, Thomson proposed that atoms are stable vortices, not in an ordinary fluid like water, but in the omni-present luminiferous aether. Stable vortices have the shape of rings with no end. In air they are easily made and made visible with smoke and are indeed surprisingly stable. According to the vortex theory, atoms are vortices in aether. The simplest one is a single ring, which was hydrogen. More complicated forms, called knots represented the other elements.

Fig. 8.1 Various vortex knots, each represents another element. From Wikimedia Commons, public domain.

Fig. 8.2 Lord Kelvin (1824-1907). From Wikimedia Commons, public domain.

At the end of the nineteenth century, in 1897, Joseph John Thomson discovered the electron. It allowed him to further refine the scientific model of the atom and it made an end to the vortex theory. In Thomson’s view, an atom had internal structure: the electrons were moving in it. As electrons have a negative charge and atoms are neutral, there must be a balancing positive charge in an atom as well. Thomson had no idea what that would be and he figured that the positive charge was everywhere in the atom (that he thought of as being a sphere), with the electrons moving inside that sphere as tiny particles. From this picture, the Thomson model got its name: the plum pudding model, although it is a bit misleading as the idea was that the positively charged sphere was more a liquid in which the electrons ‘float’ than a solid.

Fig. 8.3 Plum pudding model according to Joseph Thomson. From Wikimedia Commons, public domain.

Fig. 8.4 Joseph John Thomson (1856-1940). From Wikimedia Commons, public domain.

The model did not hold very long as we will see in the next paragraph. Nevertheless, it marks the start of physicist becoming really interested in an atom theory.

8.2. Rutherford’s scattering experiment

8.2.1. Introduction

The plum pudding model was abandoned in 1911. In 1909 Ernest Rutherford (1871-1937), a former student of Joseph Thomson, performed an ground-breaking experiment. Rutherford had been working on the newly discovered radio-activity of certain elements. He discovered that there were two types of radiation that were different from the X-rays. He called them 'alpha' and 'beta' rays and later proved that 'alpha' rays consisted of He-nuclei. Rutherford in cooperation with Frederick Soddy was the first one to prove Marie Curie's conjecture that radioactivity was an atomic phenomenon, which could lead to changes in the atom itself, from one element to another. Prior to that, the atom was seen as the ultimate, indestructible form of matter: atoms could not change from one form (element) to another.

Fig. 8.5 Marie Curie (1867-1934). From Wikimedia Commons, public domain.

Rutherford together with Hans Geiger (one of the inventors of what we now call the Geiger counter) and Ernest Marsden, built an apparatus that could count the alpha particles. Moreover, he could show that the alpha particles were He-nuclei with a positive charge of 2e. In 1917 he showed that Nitrogen could become Oxygen by bombarding it with the alpha particles. This was the first time that someone succeeded in artificially changing one element into another.

8.2.2. Scattering at a gold foil

As mentioned Rutherford is responsible for overthrowing the plum pudding model and replacing it by our modern view: an atom is made of a tiny, positively charged nucleus with the electrons orbiting around it.

The start was formed by Rutherford’s observation that some of the alpha-particles were deflected by the thin metal sheet in front of his alpha-counter. This puzzled him as the plum pudding model could not explain this. Hence, Rutherford, Geiger and Marsden set up an experiment in which they led the alpha particles scatter at a very thin gold foil. The experimental setup is schematically depicted in Fig. 8.6. A radioactive source emits alpha particles. The source is placed in a lead box to shield the experimenter from the radiation. The Source would emit \(\alpha\)-particles through a small diaphragm onto the gold foil. The diaphragm made sure that all \(\alpha\)-particles were traveling on the same line. After moving through the gold foil, the particles could be deteced by looking via a microscope at the tiny light flashes an \(\alpha\)-particle caused when hitting the detection screen. The microscope & detection screen could be placed under an angle with the original trajectory of the \(\alpha\)-particles. By measuring at all possible angles, the scattering of the \(\alpha\)-particles by the gold foil could be completely mapped and quantified.

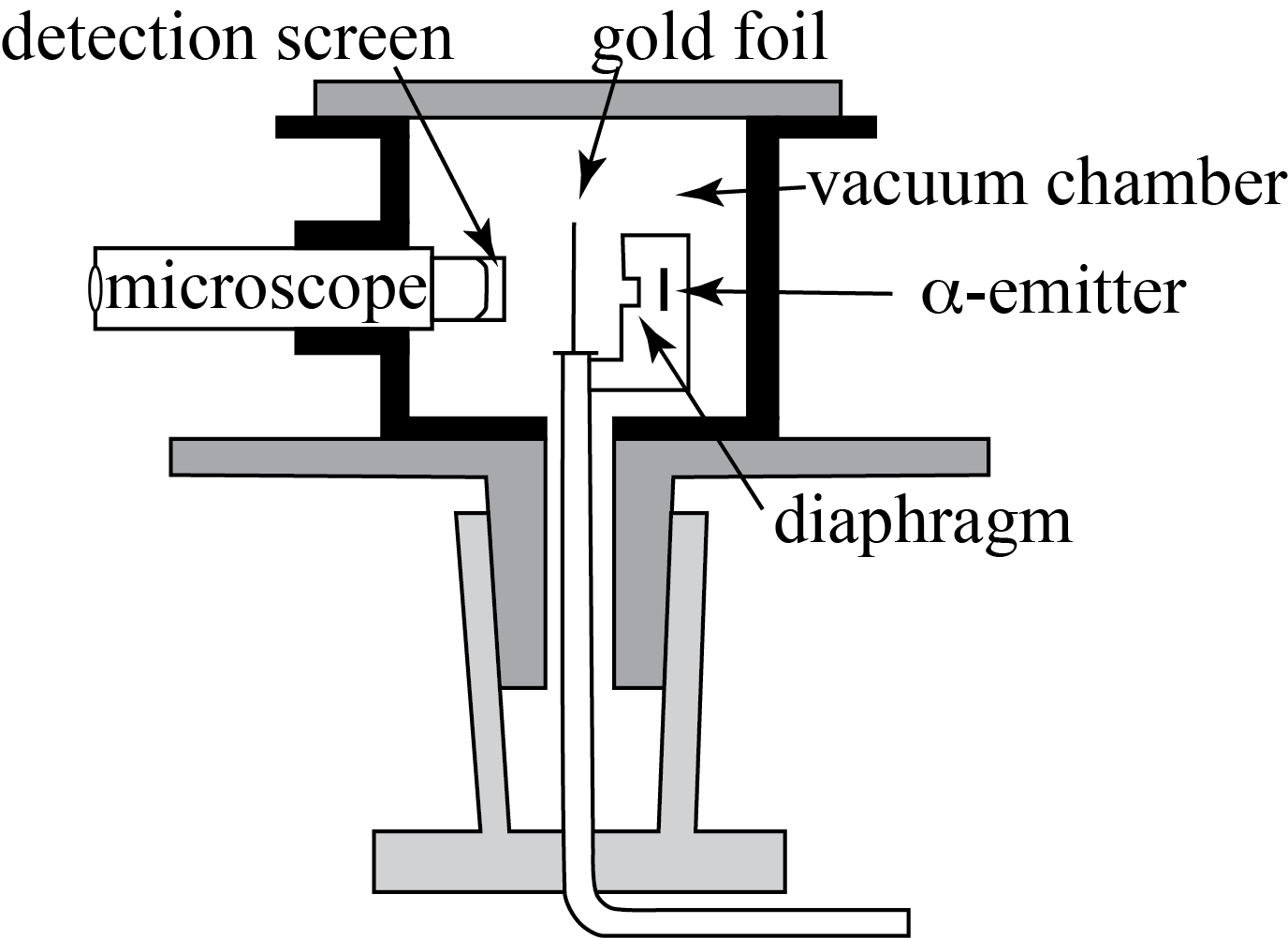
Fig. 8.6 Experimental Setup of \(\alpha\)-scattering at a gold foil.

Fig. 8.7 Ernest Rutherford (1871-1937). From Wikimedia Commons, public domain.

The story goes, that Rutherford’s students would, together with Geiger, do the measurements as an assignment of their studies. The principle is simple: set the microscope under a known angle and, for a given period in time, count the number of hits. Repeat this for the next angle of the microscope. Obviously, the first measurements where all done on the side of the foil opposite to the \(\alpha\)-emitter. Based on the plum pudding model one was expecting only small deviations of the undisturbed trajectory.

When the experiments were basically done, so goes the story, still a student was left over that also needed an assignment. One of Rutherford’s assistant suggested that this student would then measure with the microscope at the same side of the foil as the \(\alpha\)-emitter. They did not expect anything to see, but they needed an assignment for this student. Whether the story of the student assignments is true or not, fact is that the team found also hits on the detector for angles of about 180\(^\circ\). That is, some \(\alpha\)-particles seem to bounce back from the foil!

There is no way that the plum pudding model could explain this. The argumentation to show that, goes as follows.

1. The size of the atoms of gold is known: they are on the order of

   \(r_0 \approx 10^{-10}\)m.
   This value can be found from the density of gold, the mass of a gold atom and the mass and volume of the gold foil (or any other amount of gold). By treating the atoms as small spheres that are stacked back to back, the size of the atom is easily found.

2. An $\alpha$-particle has a charge of 2e and is deflected by a gold atom due to the charge of the gold atom. As gold has number 79 in the periodic table, we know that the charge of a gold atom is +79e in the 'plum pudding' and -79e of all electrons floating in the pudding.
   However, an $alpha$-particle is much heavier than an electron. Hence in the Coulomb interaction between the

   \(\alpha\) -particle and an electron, the acceleration (or deflection) of the ‘heavy’ \(\alpha\)-particle is negligible: the electrons are pushed out of the way (or actually attracted); they don’t influence the trajectory of the \(\alpha\)-particle.
   It is the positive charge of the pudding itself, that does the deflection. The atom (i.e. the pudding) can not move out of the way as it is part of the gold foil which is many orders of magnitude heavier than the incoming particle.
   We will estimate the maximum deflection of an \(\alpha\)-particle. First we need to find the force from the positive charge of a gold atom on a particle. Assume the particle is at a distance \(r\) from the center of a gold atom. See Fig. 8.8.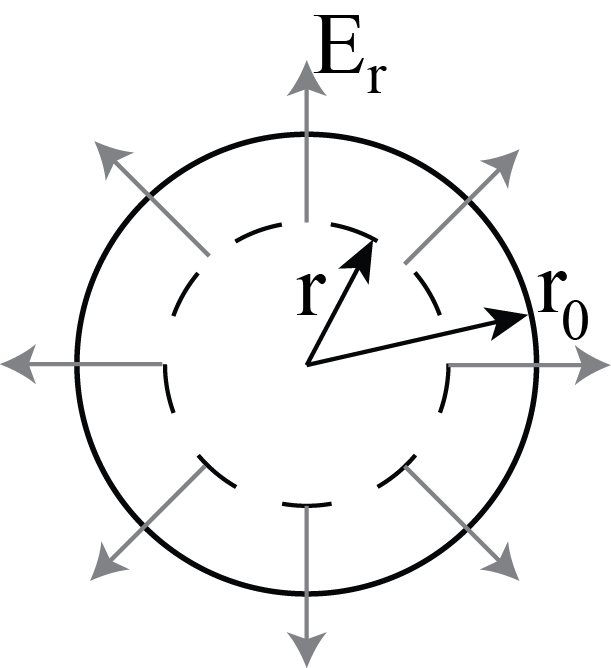

   

   Fig. 8.8 Electric field inside a gold atom according to the plum pudding model.

   We can use spherical symmetry and Gauss’ law for the electric field:

   \[ \iint \vec{E} \cdot d\vec{\sigma} = \frac{Q(r)}{\epsilon_0} \rightarrow 4\pi r^2 E_r = \frac{1}{\epsilon_0} \frac{4}{3}\pi r^3 \rho \rightarrow E_r = \frac{\rho}{3 \epsilon_0}r \]

   with \(\rho \) the positive charge density of the atom.

   From the electric field, we compute the force on the particle :

   \[ F_c = q_\alpha E_r = \frac{q_\alpha \rho}{3\epsilon_0} r \leq \frac{q_\alpha \rho}{3\epsilon_0} r_0 \]

   If we put back in the total charge of the gold atom, \(Q_g\), we find that the force on the \(\alpha\)-particle is always smaller than:

   \[ F_c \leq \frac{q_\alpha Q_g}{4 \pi \epsilon_0} \frac{1}{r_0^2} \]

   The deflection of the particle is biggest if the Coulomb force is perpendicular to the trajectory. So, we take that for our estimate. The true effect, when passing through the atom, will be smaller.

3. It is easiest to compute the change of momentum. The particle comes in with a know momentum $p$. If the change in momentum

   \(\Delta p\) is much smaller than \(p\) itself, the deflection will be small.

   

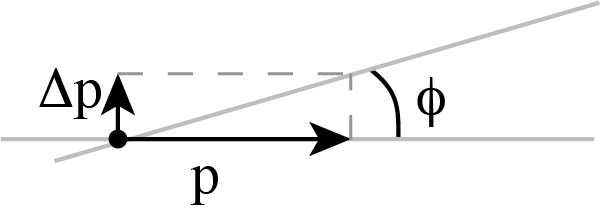
   Fig. 8.9 Relation of angle of deflection and change in momentum.

   \[\tan \phi = \frac{\Delta p}{p} \Rightarrow \phi \approx \frac{\Delta p}{p} \text{ if } \phi \ll 1\]
4. The momentum change is due to the force working for a time period

   \(\Delta t\) on the particle:

   \[ dP = Fdt -\rightarrow \Delta p \approx F_c \Delta t\]

   The time the particle is in the atom is estimated by

   \(\Delta t \approx \frac{2r_0}{v_0} \) with \(v_0\) the velocity of the incoming \(\alpha\)-particle. Again we assume that the change in momentum is small.

5. If we put everything together, we find:
   \[ \frac{\Delta p}{p} \ll \frac{q_\alpha Q_g}{4 \pi \epsilon_0} \frac{1}{r_0^2} \cdot \frac{2r_0}{v_0} = \frac{q_\alpha Q_g}{r \pi \epsilon_0} \frac{1}{r_0 v_0} \ll 1\]

   We have used the known charge of a gold atom (79e) and that of the \(\alpha\)-particle, the radius of the gold atom and the incoming velocity of the \(\alpha\)-particle, \(v_0 \approx 1.6 \cdot 10^{7}\)m/s.

With this estimate and the fact that Rutherford’s gold foil was about 400 atoms thick, there is no way that we can explain \(\alpha\)-particles bouncing back.

Rutherford and his colleagues, had no other option than concluding that the positive charge of the gold atom must be confined to a much smaller part of space. After all, the only parameter in our estimate that is not measured is \(r_0\). That was estimated based on the plum pudding model.

They redid the calculation, but now with \(r_0\) as a free parameter to be backed out of the calculation. They changed the requirement of small scattering angles (i.e. small deviation from the original path) to the experimental finding that scattering angles of about 180\(^\circ\) were possible. That gave that \(r_0\) is on the order of \(10^{-14}\)m.

Conclusion: the atom has a nucleus that is much smaller than the size of the atom that contains all positive charge. The electrons must orbit this nucleus as a mini-solar system. These electrons ‘define’ the size of the atom.

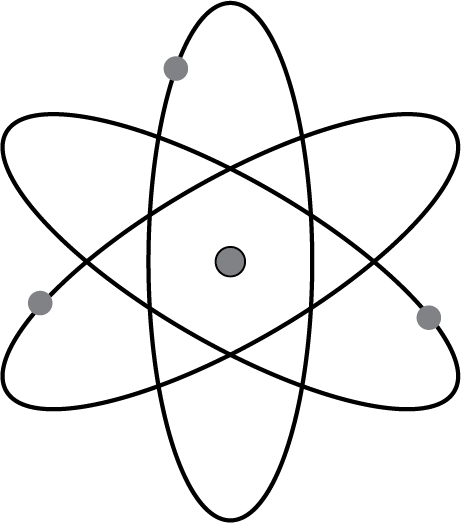
Fig. 8.10 Rutherford’s model of an atom.

This new model would spark a whole new set of questions, helping for one of the biggest changes in physics: Quantum Theory.

8.2.3. Collapse of matter?

An immediate consequence of this new view on atoms and matter came from the analogy with Newton’s work on the solar system and the Kepler Laws. As both Gravity and Coulombs forces are central, conservative forces and are inversely proportional to the square of distance from the two interacting particles

\[ \vec{F}_g = - G \frac{m_1 m_2}{r_{12}^2}\hat{r_{12}} \]

\[ \vec{F}_C = \frac{1}{4\pi \epsilon_0} \frac{q_1 q_2}{r_{12}^2}\hat{r_{12}} \]

the motion of a ‘tiny’ planet around the ‘massive’ sun is mathematically completely analogous to that of a ‘tiny’ electron around its ‘massive’ nucleus.

Thus an electron orbits the nucleus in an ellipse. Consequently, it is in a permanent state of acceleration. However, from Maxwell’s theory of Electro-Magnetism it is well known (already in the time of Rutherford as the theory of Maxwell dates back to around 1860) that accelerating charged particles radiate energy in the form of electro-magnetic waves. This means that the electron constantly looses energy and thus moves to an elliptical orbit closer to the nucleus until, eventually, its orbit collapses onto the nucleus. This process would go very fast and matter in its present form could not exist. Now we know, that the idea of an atom being a miniature solar system is wrong. But out of questions and dilemma’s as these grew very quickly quantum mechanics opening a whole new world and a completely different picture of things at the small scales. A world with new rules and new consequences, where our intuition based on daily life and large scale structures composed of many, many atoms fails.

8.3. Scattering Theory

The work of Rutherford and co-workers forms the start of a new branch of physics: nuclear physics. By using radiation in the form of X-rays (i.e. high energy photons) and electrons or protons, physicists are able to probe the internal properties of molecules, atom, nuclei and even elementary particles (or at least, what we once thought were elementary particles).

The idea is to send high energy particles towards the object of investigation and look at the scattering that is a consequence of the interaction between the object and the incoming particles. The internal structure of the object dictates the scattering. Thus, by measuring the scattering features and back tracing the underlying physical interaction can be found.

It is done with facilities of a very large scale to research particles at the smallest scales. For instance, in CERN researchers accelerate particles (protons, electrons, etc) to velocities almost the speed of light. Then, they let these particles collide, that is undergo interactions involving enormous amounts of energy, and measure the fragments and all kind of exotic particles that result from these collisions.

Fig. 8.11 Circular Accelerator of CERN depicted in its environment. ESO/José Francisco, licensed under CC-BY 4.0.

The principles used in scattering can be illustrated by revisiting Rutherford’s experiment.

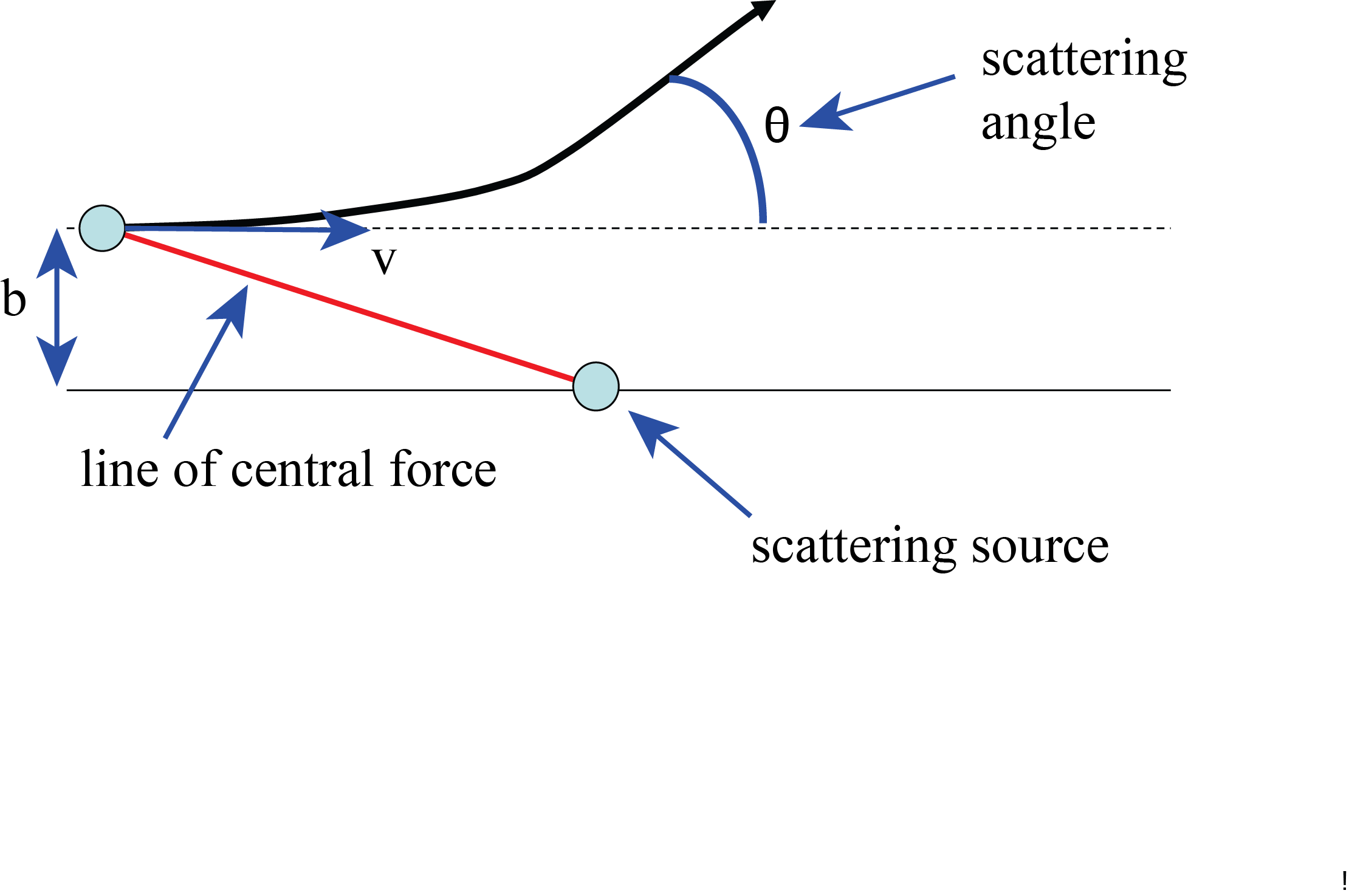
Fig. 8.12 Scattering of an incoming particle at a fixed source.

Consider Fig. 8.12: a particle of mass \(m\) and velocity \(v\) is moving towards a fixed second particle. The latter is fixed in the origin and act like a force-source. The force is central, i.e. works along the direction of the red line in Fig. 8.12. In the drawing the forces is repelling and the incoming particle will deviate from its straight line. Eventually it will continue moving over a straight line, when the influence of the force is no longer felt. The angle of the new direction with the incoming one, is \(\theta\), the scattering angle. We are looking for the relation between \(b\), the distance at which the incoming particle would have passed by the origin if there was no force and the scattering angle \(\theta\).

Fig. 8.13 left: scattering in 2D, right: scattering in 3D.

In Fig. 8.13 scattering in a 2D world and in the 3D world is schematically depicted. In the 3-dimensional world the scattering takes place in the solid angle \(d\theta\). Like the 2d equivalent, where the scattering angle can go from 0 to \(2\pi\) (that is the full circle), in 3d it goes from 0 to \(4\pi\) reflecting that it is now a full sphere.

8.3.1. Coulomb Scattering

We will take the case of scattering of an electrically charged particle due to the Coulomb force.

\[ \vec{F}_C = \frac{1}{4 \pi \epsilon} \frac{q_1 q_2}{r^2} \hat{r} = \frac{k}{r^2} \hat{r} \]

This is a central force (we have fixed charge \(q_2\) in the origin). Thus, the angular momentum is conserved.

\[ \vec{l} = cont \Rightarrow l = mr^2 \dot{\phi} = cst \]

Moreover, the force is conservative, thus a potential exists

\[ V(r) = -\int_\infty ^r \frac{k}{r^2} dr = \frac{k}{r} \]

and the mechanical energy is conserved

\[E_{kin} + V = E_0 \Rightarrow \frac{1}{2}m\dot{r}^2 +\frac{l^2}{2mr^2} + \frac{k}{r} = E_0 \]

So far, this is completely analogues to the Kepler case. Here we will proceed with a different solution strategy. From the conservation of energy we get $\( \frac{dr}{dt} = \sqrt{ \frac{2}{m} \left ( E_0 - \frac{k}{r} - \frac{l^2}{2mr^2} \right ) } \)$

Look for a solution of the form \(r(\phi (t))\) and thus write

\[\frac{dr}{dt} = \frac{dr}{d\phi } \frac{d\phi }{dt} = \frac{dr}{d\phi } \frac{l}{mr^2} \]

where we have used that \(l\) is a constant. This gives:

\[\begin{split} \begin{split} d\phi &= \frac{l}{r^2} \frac{dr}{\sqrt{2m \left ( E_0 - \frac{k}{r} - \frac{l^2}{2mr^2} \right ) }} \\ &= \frac{-ld(1/r)}{\sqrt{2m \left ( E_0 - \frac{k}{r} - \frac{l^2}{2mr^2} \right ) }} \\ &= \frac{-d(1/r)}{\sqrt{\frac{2mE_0}{l^2}- \frac{2mk}{l^2}\frac{1}{r}- \frac{1}{r^2}}} \end{split} \end{split}\]

Substitute \(s = 1/r \) and write the terms under the square root into a square:

\[\begin{split} \begin{split} d\phi &= \frac{-d(s)}{\sqrt{\frac{2mE_0}{l^2}- \frac{2mk}{l^2}s- s^2}} \\ &= \frac{-d(s)}{\sqrt{\underbrace{\frac{2mE_0}{l^2} +\frac{m^2 k^2}{l^4}}_{=\beta ^2} - \left ( \underbrace{s +\frac{mk}{l^2}}_z \right )^2}} \\ &= \frac{-dz}{\sqrt{\beta^2 - z^2}} \end{split} \end{split}\]

This has as solution \(\sin\) and \(\cos\). We can write it as

\[z = \beta \cos (\phi - \phi_0 ) \]

If we now substitute back we obtain:

\[ \frac{1}{r(\phi )} = -\frac{mk}{l^2} + \beta \cos ( \phi - \phi_0 ) \]

Fig. 8.14 scattering path in 2D, \((r,\phi )\) coordinates.

In Fig. 8.14 the solution is depicted. Note that the incoming \(\alpha\)-particle now comes from the right. The reason for this is, that it is somewhat easier to make the final step: we haven’t specified the initial conditions, so our solution still contains two unknown (integration) constants. The first one is easy to spot: \(\phi_0\). The second one is in the value of the energy, \(E_0\) which is not specified.

This can be easily cured:

\[\begin{split}\text{initial condition : } \phi = 0, r=\infty, \dot{r} = -v \\\text{initial distance above }x\text{-axis} = b \end{split}\]

With this the energy is now given, as well as the angular momentum \(l = mbv\)

We can also find \(\phi_0\): substitute the initial condition in our \(r(\phi )\) solution:

\[\frac{1}{\infty } = -\frac{km}{l^2} + \beta \cos \phi_0 \]

Thus \(\beta \cos \phi_0 = \frac{km}{l^2} \)

Moreover, if we take the derivative of \(r\), we find another relation between \(\beta\) and \(\phi_0\):

\[ \frac{dr}{dt} = \frac{l}{mr^2} \frac{dr}{d\phi} = -\frac{l}{m} \frac{d(1/r)}{d\phi} = -\frac{l}{m} \cdot -\beta \sin ( \phi - \phi_0 ) \]

Use again our initial condition: \(\phi = 0 \rightarrow \frac{dr}{dt} = -v\) and the last two equations give:

\[-v = -\frac{l}{m} \beta \sin \phi_0 \Rightarrow \beta \sin \phi_0 = \frac{mv}{l}\]

If we combine both expressions for \(\phi_0\), we get

\[\cot \phi_0 = \frac{km}{l^2} \cdot \frac{l}{mv} = \frac{k}{mbv^2}\]

In other words: \(\phi_0\) is not a free constant, but given by the initial conditions, i.e. \(v\) and \(b\).

Now we need to make the connection to the scattering angle \(\theta\). For that we look at Fig. 8.15.

Fig. 8.15 Relation of the scattering angle \(\theta\), \(\phi_0\) and \(r_{min}\).

First, we check what the value of \(r(\phi)\) is, if \(\phi = \phi_0\):

\[ \frac{1}{r(\phi )} = -\frac{km}{l^2} + \beta \cos (\phi - \phi_0 ) \Rightarrow \frac{1}{r(\phi_0)} = -\frac{km}{l^2} + \beta\]

It is clear, that this is the minimum value, \(r_{min}\) of \(r\), i.e. the closest the \(\alpha\)-particle gets to the origin. However, the angle between the incoming direction and the outgoing direction of the particle must be \(2\phi_0\). We can see this, because the incoming and outgoing trajectory are identical, or rephrased, the problem must be symmetric around the line from the origin to the point of closet approximation. We can conclude this from the argument, that if we reverse the velocity of the particle once it has disappeared to infinity, the particle will travel over exactly the same trajectory back to its original position before the scattering experiment. Why? Look at the governing equation that we started with: the conservation of energy. That is quadratic in \(v\) and thus, if we change at the end from \(v\) to \(-v\) we will get exactly the same solution but now run backwards.

Our main conclusion of the above is:

\[2\phi_0 + \theta = \pi \Rightarrow \tan \frac{\theta}{2} = \tan \left ( \frac{\pi}{2} - \phi_0 \right ) = \cot \phi_0 = \frac{k}{mbv^2}\]

And we finally have our relation that couples \(b\) to \(\theta\):

\[ b(\theta) = \frac{k}{mv^2} \frac{1}{\tan \frac{\theta}{2}} \]

Obviously, in scattering experiments with elementary particles as done in CERN, one of the question is: what kind of interaction is going on. So, in a real experiment \(b(\theta )\) is measured and from the gathered data physicist try to understand the internal structure of objects in the scattering experiments and get a grip on the interaction forces and energies involved.

With the above result from our scattering theory, we can re-visit Rutherford’s experiments. We had already discussed that the maximum effect and thus the maximum scattering angle, is realized when the \(\alpha\)-particle is passing the plum pudding atom at exactly a radius \(r_0\) distance.

Rutherford and co-workers have probably done a similar calculation:

\[ \tan \frac{\theta}{2} \approx k \frac{1}{r_0} \frac{1}{mv^2} = \frac{1}{4\pi \epsilon_0} \frac{2e \cdot 79e}{r_0} \frac{1}{mv^2} \approx 2\cdot 10^{-4} )\]

And thus we find:

\[ \theta \leq 0.02^\circ \]

With a gold foil of only 400 atoms thick, the maximum scattering angle they could expect, based on the plum pudding model, is

\[ \theta \approx 400 \cdot 0.02^\circ \lt 10^\circ \]

However, they found \(90^\circ\) and even \(180^\circ\). The plum pudding theory could not hold! If they tried to change the only parameter they could: \(r_0\), they found \(r_0 \approx 10^{-14}\)m to get scattering of 180\(^\circ\). The conclusion was inevitable: atoms are miniature solar systems, empty with a tiny nucleus in the center.