8.4. Exercises#
Each exercise carries the difficulty level indication:
[*] Easy
[**] Moderate
[***] Advanced
The highest difficulty level is meant for students who wish to challenge themselves and/or have previous experience in programming.
Exercise 8.5 ([*] Calling functions)
Using the given function which calculates the mean, find the list which has the highest mean and the value of that mean. Using the function we do not need to write the logic of calculating the mean again for every list, but instead we put the logic in one function and re-use the same function for every list.
As always, draft the pseudocode before you start coding in Python.
Hint: use a for loop and track the highest mean.
list1 = [3, 5, 7, 9, 2, 4, 6, 8, 10, 1, 3, 5]
list2 = [7, 9, 2, 4, 7, 5, 3, 1, 8, 6]
list3 = [2, 4, 6, 9, 10, 3, 5, 6, 9]
list4 = [1, 3, 5, 7, 9, 1, 3, 5, 7, 2, 4, 6, 8, 10]
list5 = [4, 6, 8, 10, 2, 4, 6, 8, 10, 1, 3, 5, 7, 9]
numbers_lists = [list1, list2, list3, list4, list5]
def calculate_mean(list_numbers):
sum = 0
for i in list_numbers:
sum += i
return sum / len(list_numbers)
# Your code here
Exercise 8.6 ([*] BMI)
Body mass index (BMI) can be calulated as: \(BMI = weight / height^2\)
Exercise A: Calculate the BMI of various people using a for loop and return
BMIs as a list.
weights = [60, 76, 55, 90]
heights = [1.70, 1.80, 1.65, 1.90]
bmi = []
# Your code here
print(bmi)
Exercise B: Imagine later we want to calculate the BMI of another list of people. We could copy the code, but if we want to do this more often it is better to write a function and avoid code duplication.
Rewrite the code into a function called calculate_bmi, then call the function
and save the output in the variable bmi. Finally, print the results.
weights = [60, 76, 55, 90]
heights = [1.70, 1.80, 1.65, 1.90]
def calculate_bmi( # Your code here):
# Your code here
return # Your code here
bmi = calculate_bmi( # Your code here)
print(bmi)
Exercise 8.7 ([*] Local vs. global)
This exercise will help you understand the difference between local and global variables in Python. You will see how variable scope affects the behavior of your code. You will be given a block of code. Pay attention to how variables are used and modified. Run the code and observe the output.
counter = 10
def increment_counter():
counter = 5 # Local variable
counter += 1
print("Inside function, counter:", counter)
increment_counter()
print("Outside function, counter:", counter)
Now modify the function increment_counter so that it uses the global variable counter instead of creating a local variable.
# Your altered code here
Exercise 8.8 ([**] Motif finding)
It’s often useful to know if a given DNA sequence contains a specific
motif: in Python, a variable should be True if the motif is found
and False otherwise. DNA sequences are strings composed of the characters
A, T, C, and G. A motif is a specific sequence of these characters.
This is an example of how you can find this:
dna_sequence = "ATGCGATACGCTTGA"
motif = "GCT"
if motif in dna_sequence:
found = True
else:
found = False
print("Motif found:", found)
We might want to do this for multiple DNA sequences or multiple motifs, and different combinations of these. This is where functions come in: with functions, this logic can easily be applied to any combination of DNA sequences and motifs.
dna_sequence = "ATGCGATACGCTTGA"
motif = "GCT"
def find_motif(dna, motif):
found = False
# Your code here
return found
found = find_motif(dna_sequence, motif)
print("Motif found:", found)
Exercise 8.9 ([**] Gravity)
In this exercise we write a function to calculate the gravitational force. The gravitational force is given by the following formula:
\(F_g = \frac{G * m_1 * m_2}{r^2}\)
Exercise A:
Imagine we want to make a function which calculates the gravity on Earth.
Let’s call this funcion gravity_earth.
Which of the variables become constants and which should be input parameters?
Hint: You will need to Google to find the required constant values for this function.
# Your code here
Exercise B:
Apply your function (gravity_earth) to calculate the gravitational force on an
object with mass of 10 kg.
m = 10 # kg
# Your code here
Solution
The simplified gravity (according to Newton) uses \(F = m \times a\) with \(a\) set to 9.81, so the solution would be 98.1 N. However, the more basic (i.e., relativistic) formula we use in this exercise with the most current known values of the Earth’s mass and radius and \(G\) constant give a slightly different number of 97.9 N.
Exercise C: Imagine we want to compare the gravitational force an astronaut experiences on different planets. Given that the astronaut weighs 90 kg, write a function which calculates the gravitational force on the astronaut on different planets.
# Your code here
Exercise 8.10 ([*] Mutable parameters)
In this exercise, you will explore how variables behave when passed to a function, and how mutating a list (which is a mutable object) inside a function affects the original list defined outside the function. You will also observe the behavior of immutable objects such as integers and strings when passed to a function.
You are given a list of cell counts from different biological samples. The function you will implement will add a new value to this list to update it with new data. Additionally, the function will attempt to modify an integer variable, but notice the difference in behavior between the mutable list and the immutable integer.
We have a function update_sample that:
Appends a new value to a list of cell counts (this list is defined outside the function).
Attempts to modify a variable (an integer) defined outside the function.
After running this code, observe the behavior of the list and the integer variable outside the function.
# Global list (mutable) and integer (immutable) defined outside the function
cell_counts = [100, 120, 130]
total_samples = 3
def update_sample(new_count, cell_counts = cell_counts, total_samples = total_samples):
# Add new sample count to the list (mutable object)
cell_counts.append(new_count)
# Attempt to modify total_samples (immutable object)
total_samples += 1 # This will not affect the global variable!
# Call the function with a new sample count
update_sample(150)
# Print the list and the integer outside the function
print("Updated cell counts:", cell_counts) # Expected to be updated
print("Total samples:", total_samples) # Expected to NOT be updated
assert cell_counts == [100, 120, 130, 150], "cell counts should be updated"
assert total_samples == 4, "total samples should be updated"
Why is the list cell_counts updated, but total_samples does not change?
Modify the code to fix the behavior of total_samples so that it updates correctly.
Hint: You might need to use the global keyword or return the updated value from the function.
Exercise 8.11 ([**] Reverse complement)
In this exercise we will create a function which returns the reverse complement of a DNA sequence. This is a useful case to create a function as finding the reverse complement of any sequence follows the same logic, so instead of copy-pasting the code, we create a function and call it every time we need to find the reverse complement of a sequence.
The function should be able to find the reverse complement of any DNA sequence
(so also for varying lengths). Name the function reverse_complement.
You can assume that DNA consists only of A, T, C and G.
After you’ve defined the function, call it for the given DNA sequence and print the output.
Example of a reverse complement:
DNA: ACCTGTAAA
Reverse Complement: TTTACAGGT
Hint: A list or string can be reversed using reversed_var = var_name[::-1]
DNA = "TTGTGATATAGGTACCAGTCACGTTGACGTAGTCTAGCTAGCATGTCAAGCACTTGAA"
# Your code here
Exercise 8.12 ([**] Documenting functions)
Note: this exercise contains an introduction, which is absent from the downloadable exercise (.py) file.
Introduction
When learning how to code it is not only important how to make code that works, but also that the code is understandable. This is important in collaborations and even in solo projects (since after a while you can get confused with your own code which you wrote earlier). Generally, this is done with comments throughout your code, but there are two ways which are specific to functions: docstrings and type hints.
A docstring is a special kind of comment in Python used to describe what a function does. It is placed directly below the function definition and enclosed in triple quotes (“””). A well-written docstring typically includes:
A brief description of what the function does.
Information about the parameters the function takes (names, types, and descriptions).
A description of the return value, including its type.
Any exceptions that the function might raise (if applicable).
Example of a docstring:
def add(a, b):
"""
Adds two numbers together.
Parameters:
a (int or float): The first number.
b (int or float): The second number.
Returns:
int or float: The sum of the two numbers.
"""
return a + b
Type hints (also called type annotations) are a way to explicitly specify the data types of variables, function parameters, and return values. They help in improving code readability and can assist tools that perform type checks, which can catch potential errors before running the code.
Type hints do not affect how the code runs, but they provide additional information for the developer and anyone reviewing the code.
Example:
def add(a: int, b: int) -> int:
"""
Adds two integers together.
Parameters:
a (int): The first integer.
b (int): The second integer.
Returns:
int: The sum of the two integers.
"""
return a + b
In this example:
The parameters a and b are expected to be of type int.
The function is expected to return a value of type int.
In this exercise, we work with a function that calculates a person’s heart rate training zones based on their age and resting heart rate. The function uses the Karvonen formula to calculate the target heart rate zones for light, moderate, and intense exercise.
The formula is:
Target_HR = Resting_HR + (Maximum_HR − Resting_HR) × Intensity
where:
Maximum_HR = 220−age
Intensities: light (50%), moderate (70%), intense (85%).
Exercise A: Add the correct type hints and create a docstring for the function given.
Your type hints should be the same as those given in the solution. For the docstring it is mostly important to see if it contains the same elements; the wording will usually be different per programmer.
def calculate_heart_rate_zones(age, resting_hr):
max_hr = 220 - age
# Intensities for light, moderate, and intense exercises
intensities = [0.50, 0.70, 0.85]
heart_rate_zones = []
for intensity in intensities:
heart_rate_zones.append(resting_hr + (max_hr - resting_hr) * intensity)
return heart_rate_zones
# Example input parameters
age_of_person = 30 # years
resting_heart_rate = 60.0 # beats per minute
# Call the function with the example inputs
heart_rate_zones = calculate_heart_rate_zones(age_of_person, resting_heart_rate)
# Print the result
print("Heart Rate Zones:", heart_rate_zones)
Docstrings are not only useful as a summary when looking directly at the source code, but also when using functions when not looking at the source code.
We can then access docstrings using Python’s help function.
Exercise B:
Call the help function on the function that you just created the docstring for
and your docstring should be displayed.
Note: you can also do this with functions you have not created yourself, e.g.:
import numpy as np
help(np.linspace)
help(# Your code here)
Exercise 8.13 ([*] Hardcoding - cell count threshols)
One mistake which is often made in code in general, but also in functions specifically (since functions especially are designed to be generic and flexible), is hardcoding. This is where one variable is set to a specific value, which restricts the use cases of a particular piece of code.
In this exercise, you are provided with code that determines whether a sample contains a sufficient number of cells for a study. The code is hardcoded to check if the sample contains at least 100 cells, which works for some studies but not for others. Modify the code such that it would also work for studies which have different thresholds.
def is_sufficient_cells(cell_count):
# Hardcoded threshold for 100 cells
if cell_count >= 100:
return True
else:
return False
# Example 1: Study with 100 cell threshold (works fine)
sample_cell_count = 120
print("Is the sample sufficient?", is_sufficient_cells(sample_cell_count))
# Example 2: Study with 200 cell threshold (doesn't work correctly)
print("Is the sample sufficient for a study requiring 200 cells?", is_sufficient_cells(sample_cell_count))
It is important to note that not everything needs to be 100% flexible, for example, in this cases leaving the cell count hardcoded might be fine, as it might only be used by your lab which always uses the same amount, or the number is an industry standard which is always used. This makes this a consideration between flexibility and simplicity.
There is also another way to solve this using default parameters, which looks like this:
def function(force, mass = 10):
Exercise 8.14 ([*] Hardcoding - projectile motion)
One mistake which is often made in code in general, but also in functions specifically (since functions especially are designed to be generic and flexible), is hardcoding. This is where one variable is set to a specific value, which restricts the use cases of a particular piece of code.
In this exercise, you are provided with code that calculates the maximum height of a projectile based on a fixed gravitational acceleration. The code works perfectly on Earth, but fails on other planets like Mars or Jupiter, where the gravitational constant differs. Your task is to modify the code to work in any scenario by fixing the hardcoded gravitational constant.
The formula for the maximum height of a projectile is:
\(h_{max} = \frac{v_0^2 sin^2(\theta)}{2g}\)
Where:
\(v_0\) is the initial velocity
\(\theta\) is the launch angle (in degrees)
\(g\) is the gravitational acceleration
import math
def max_height(v0, theta):
# Hardcoded gravitational constant for Earth
g = 9.81 # m / s^2
theta_rad = math.radians(theta)
h_max = (v0**2 * math.sin(theta_rad)**2) / (2 * g)
return h_max
# Example 1: Earth (works fine)
initial_velocity = 50 # m/s
angle = 45 # degrees
print("Max height on Earth:", max_height(initial_velocity, angle))
# Example 2: Mars (g = 3.71 m/s², doesn't work correctly)
print("Max height on Mars:", max_height(initial_velocity, angle))
It is important to note that not everything needs to be 100% flexible, for example, in this case leaving the gravitational constant hardcoded might be fine, as it is highly likely you’re coding something which will only ever be used on Earth and it makes the function simpler to use. This makes this a consideration between flexibility and simplicity.
There is also another way to solve it using default parameters, which looks like this:
def function(force, mass = 10):
Exercise 8.15 ([*] Returning multiple values)
In this exercise we will practice using functions that return multiple values and see how to store multiple values. One common reason to return multiple values with one function is that the outputs require the same input parameters and both output values are always required for our use case. In other cases one of the outputs might be an intermediary output of the final output, but the intermediary is still useful to us.
In this example you will work with a function that calculates the perimeter and area of a rectangle. The goal is to help you understand the utility of returning multiple values from a function and how to correctly assign these values to different variables.
Exercise A:
You are provided with a function calculate_rectangle that calculates both the
perimeter and area of a rectangle given its length and width.
Your task is to call the function, capture the returned values, and correctly
assign them to the variables perimeter and area.
Print out the results to verify that you have correctly handled the function’s output.
def calculate_rectangle(length, width):
perimeter = 2 * (length + width)
area = length * width
return perimeter, area
# Given parameters
length = 5.0 # meters
width = 3.0 # meters
# Your code here
Exercise B: Do the same as in A, but with a slightly different function.
def calculate_rectangle_list(length, width):
perimeter = 2 * (length + width)
area = length * width
return [perimeter, area]
# Given parameters
length = 5.0 # meters
width = 3.0 # meters
# Your code here
Exercise 8.16 ([**] Halloween route)
For Halloween in your neighborhood, you get a list with adresses randomly distributed over a map. It is up to you to find the optimal route to pass by every house and walk the shortest distance overall.
Exercise A:
Make a function named dist which calculates the distance between the
current location and a future location.
Hint: you might want to use np.sqrt.
current_location = [0,0]
future_location = [3,4]
def dist (current, future):
# Your code here
Exercise B:
Now instead of getting one future location, you get an array with locations.
Make a function best_location to find the best future location, which is
closest to the current location.
Hint: you might want to use np.where, and feel free to reuse (part of) your
above dist function.
future_locations= np.array( [ [10,0],[10,5] , [10,-5],[-8,0], [-8,4],[-8,-4],[-2,1],[-5,2.5],[3,1.5],[7,3.5]])
# print(np.shape(future_locations))
def best_location(current, future):
# Your code here
Exercise C:
By using the previous best_location function, write code to automatically
find the most optimal route along all future_locations. Do this by repeatedly
finding the best next step.
An array, called route, should be generated, which is the optimally
rearranged version of future_locations, starting and ending at the current
location [0,0]. Whether you are correct can be directly seen after plotting
the route below.
Hint: you might want to use numpy.delete(arr, obj, axis=None)
arr: Input array
obj: Row or column number to delete
axis: Axis to delete
def find_best_location(current,future):
route = np.zeros((len(future)+2, 2))
# Your code here
return route
With this code you can visualize your route:
route = find_best_location(current_location, future_locations)
print(route)
import matplotlib.pyplot as plt
plt.plot(route[:,0],route[:,1],'*-')
plt.show()
Exercise 8.17 ([**] Black Friday)
Functions can use multiple return statements using if-else statements. The first return encountered will be the value returned from the function. For example:
def function(x):
if x >= :
return ...
elif x >= :
return ...
elif x >= :
return ...
return ...
Exercise A: In this exercise, you are calculating the total price after applying discounts. In this case the store has different applicable discounts for increasing totals:
20% off from 50 euros
30% off from 100 euros
50% off from 200 euros
Implement function calculate_discount that returns the discounted price
based on the price before discount.
Test your function by passing the following values to it:
100, 70, 250, 30, -10
# Your code here
Exercise B: Sometimes the store website does not work correctly for the store and the price before discount ends up being negative. This should not happen, so we would like the function to throw an error if the total is negative.
# Your code here
# If the code was altered correctly this code line should give an error
print("Total = ", calculate_discount(-3))
Exercise 8.18 ([**] Roman centurion)
Imagine a cruel Roman centurion (or a very smart virus), who releases only one out of all prisoners alive. He does this by removing every \(N^{th}\) prisoner, until he is left with a sole survivor.
Your task is to predict, with a given number of prisoners and value for
kill_every, which prisoner will survive.
Given the number of prisoners nb_prisoners and the kill-every number
kill_every, make a function which predicts which prisoner will survive.
For example nb_prisoners=10, kill_every=3, results in prisoner number 4
surviving:
0 1 2 3 4 5 6 7 8 9 -> kill 2
0 1 3 4 5 6 7 8 9 -> kill 5
0 1 3 4 6 7 8 9 -> kill 8
0 1 3 4 6 7 9 -> kill 1
0 3 4 6 7 9 -> kill 6
0 3 4 7 9 -> kill 0
3 4 7 9 -> kill 7
3 4 9 -> kill 4
3 9 -> kill 9
3 -> the fourth prisoner survived (note Python counts from 0)
Exercise A: Predict what is the best programming approach. Before you start programming, think about the easiest way to implement. Check the images below for three representations of possible Python implementations.
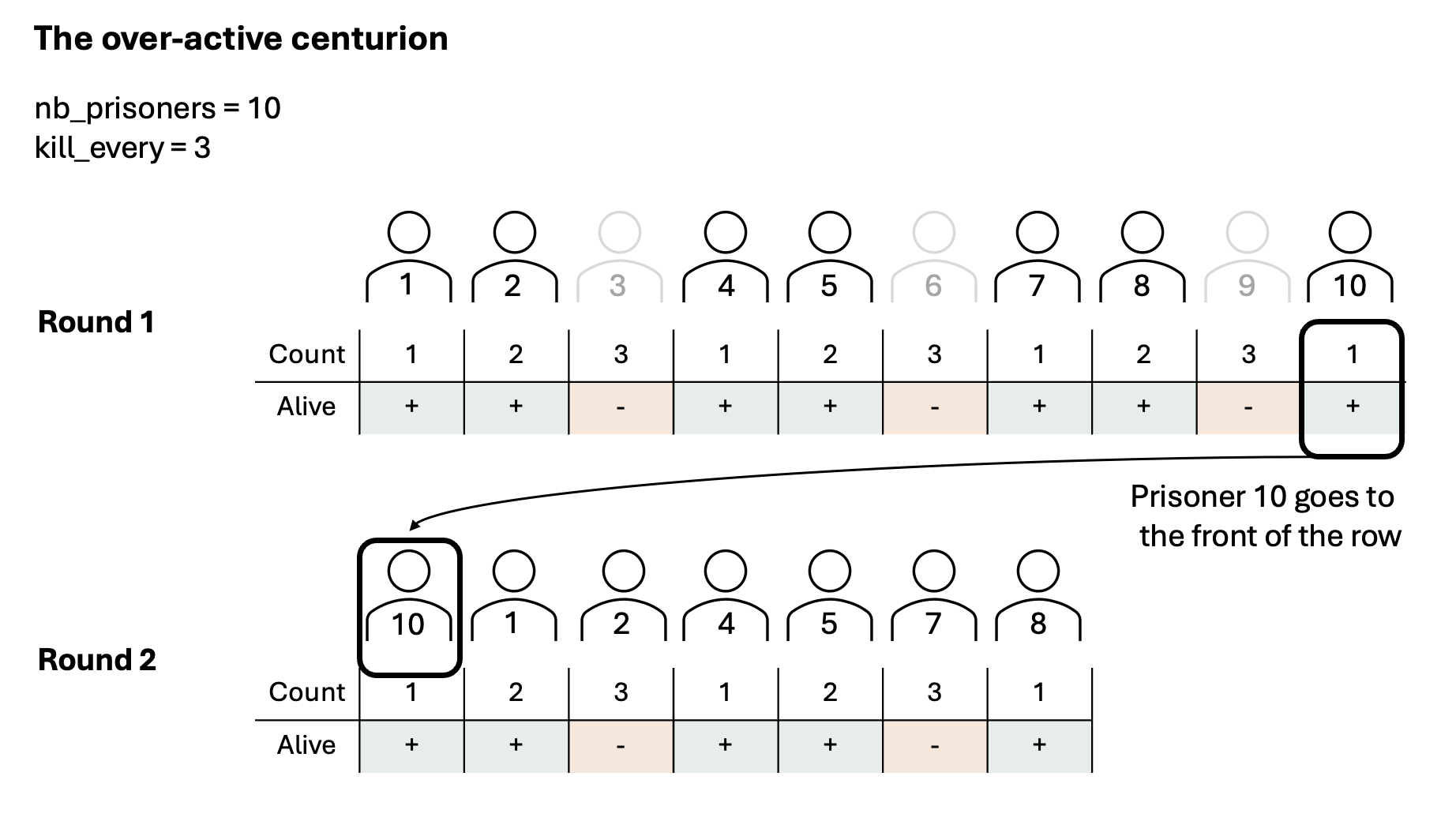
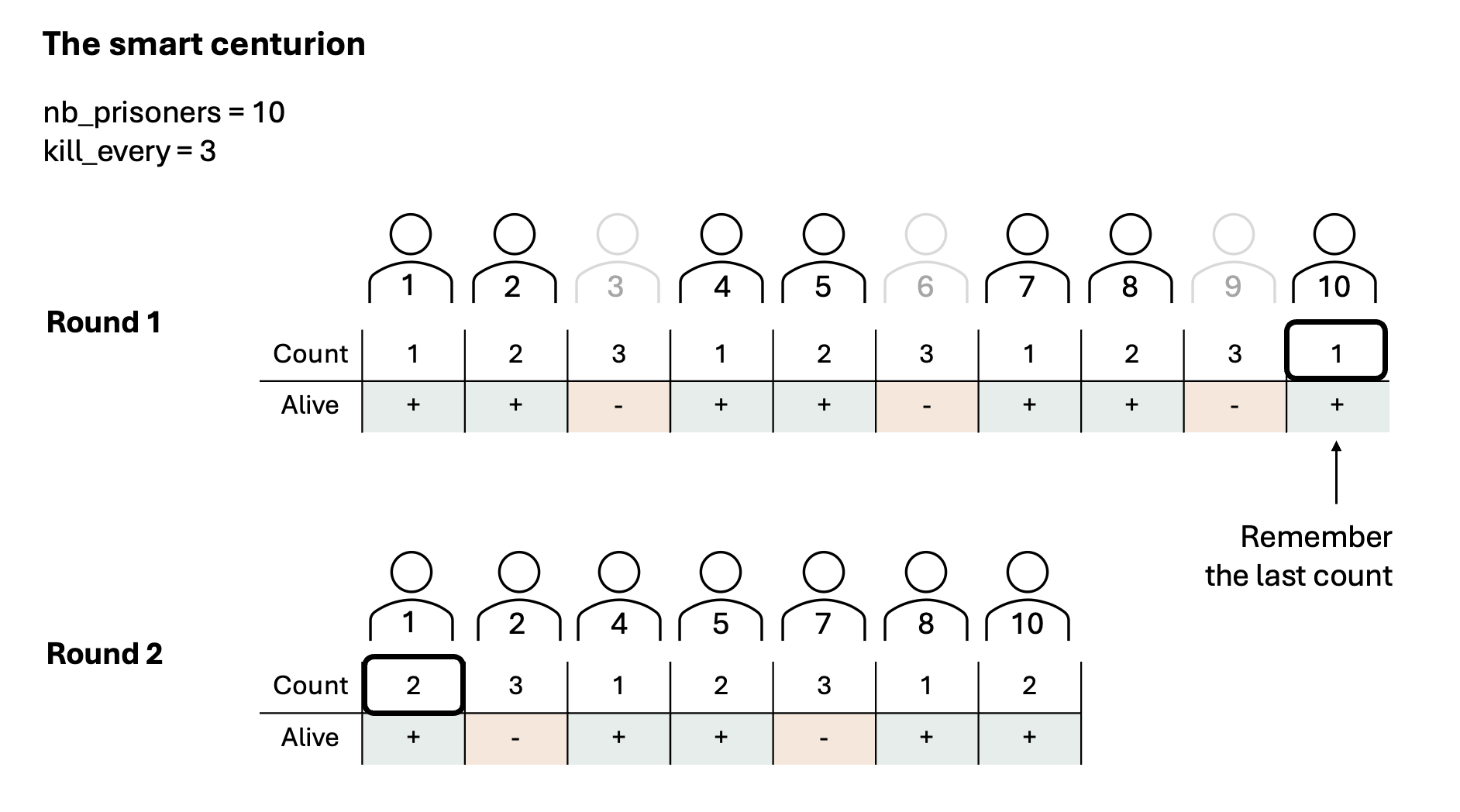
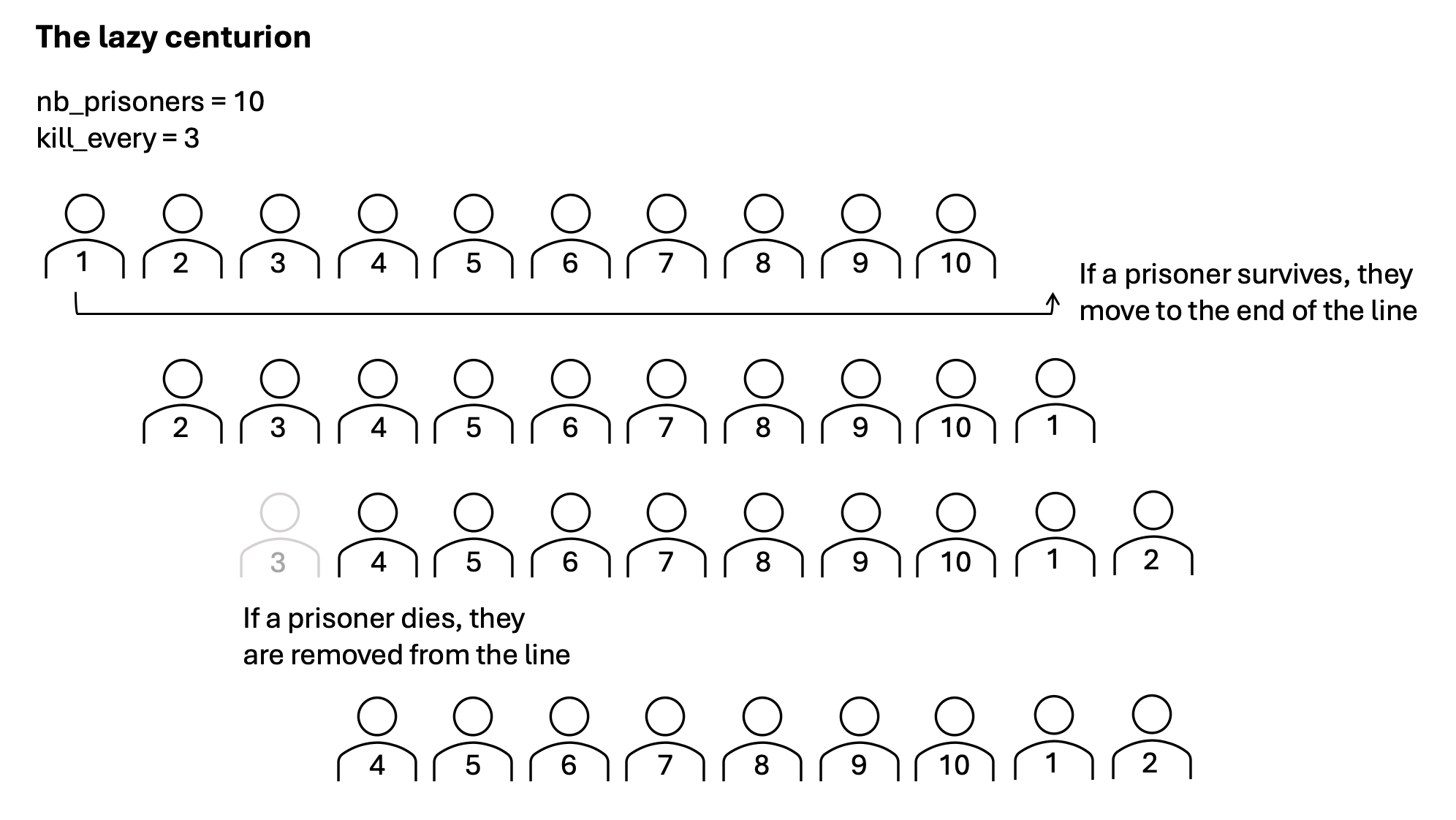
Exercise B: Implement your choice of centurion.
If you cannot choose, you are recommended to start with the lazy centurion (who sits down, lets the prisoners walk and kills every \(N^{th}\) person).
Note that stitching of NumPy arrays is done with
np.concatenate([a,b]).Write pseudocode first.
Don’t forget to check your intermediate answers, especially the ones in the second and third iteration.
Define the number of prisoners and kill_every and test your function. You can try
several combinations; you may want to start with nb_prisoners=10 and kill_every=3 from the example above.
import numpy as np
def decimate(nb_prisoners, kill_every):
# Your code here
Exercise C (Optional): Implement one or both of the other centurions.
Exercise 8.19 ([**] Central dogma)
In this exercise, you will work with genomic sequences using dictionaries, lists and strings.
Specifically, you will write a function that compares two DNA sequences and checks for certain types of mutations.
Transcription
TFIID is a protein complex essential for the initiation of transcription by RNA Polymerase II. It contains multiple subunits, including the TATA-binding protein (TBP). TBP binds specifically to the TATA box, a DNA sequence typically found in the promoter region of many genes. This binding helps position TFIID at the correct location on the DNA, which in turn helps recruit other transcription factors and RNA Polymerase II to initiate transcription.
Usually, this TATA-box sits 25 nucleotides upstream of the transcription start site. An unknown number of nucleotides later, you will find the start codon.
Chemically, DNA is transcribed from 3’ to 5’ with respect to the template strand. In bioinformatics, the convention is to store genomic data from 5’ to 3’. You may assume that the given sequence corresponds to the coding sequence.

DNA = 'TTGTGATATAGGTACCAGTCACGTTGACGTAGTCTAGCTAGCATGTCAAGCACTTGAA'
Exercise A: Transcription
Write a function transcribe that takes a DNA sequence (as string),
localises the TATA-box and transcribes the gene from the transcription start
site onwards, until the end of the given sequence. The output should be a string.
The function should not contain any for loops.
Example input: ‘TTGTGATATAGGTACCAGTCACGTTGACGTAGTCTAGCTAGCATGTCAAGCACTTGAA’
Example output: ‘GUCUAGCUAGCAUGUCAAGCACUUGAA’
Hints:
string.findmay be useful for finding the TATA-box.string.replacemay be useful for replacing T with U.
def transcribe(DNA):
# Your code here
return RNA
Translation
Next, the mRNA is translated in the ribosome, where all triplets are paired to the anticodons of charged tRNA. Note that translation only starts after the start codon AUG, which also corresponds to the first amino acid of the polypeptide: methionine. Since there are 64 possible codons and only 20 amino acids, we know that several codons can map onto the same amino acid.

Exercise B: Coding sequence
Write a function codingRNA that takes this RNA transcript, finds
the first start codon, finds the corresponding first stop codon and exports
all triplets as a list (including stop codon). The stop codons are UAA,
UAG and UGA. If there is no stop codon at the end, write 'no stop' as
final codon. If there is no start codon, return [].
Example input 1:
'GUCUAGCUAGCAUGUCAAGCACUUGAA'Example output 1:
['AUG','UCA','AGC','ACU','UGA']Example input 2:
'GUCUAGCUAGCAUGUCAAGCACU'Example output 2:
['AUG','UCA','AGC','ACU','no stop']
def codingRNA(RNA):
# Your code here
Exercise C: Translation
Write a function translate that takes this coding RNA array and translates it.
You may use the given dictionary. The output should be a string. If there
is no start codon, return ‘’. If there is no stop codon, add a dot at the end:
‘MSST.’.
conversion = {'AUA':'I', 'AUC':'I', 'AUU':'I', 'AUG':'M','ACA':'T', 'ACC':'T',\
'ACG':'T', 'ACU':'T','AAC':'N', 'AAU':'N', 'AAA':'K', 'AAG':'K',\
'AGC':'S', 'AGU':'S', 'AGA':'R', 'AGG':'R','CUA':'L', 'CUC':'L',\
'CUG':'L', 'CUU':'L','CCA':'P', 'CCC':'P', 'CCG':'P', 'CCU':'P',\
'CAC':'H', 'CAU':'H', 'CAA':'Q', 'CAG':'Q','CGA':'R', 'CGC':'R',\
'CGG':'R', 'CGU':'R','GUA':'V', 'GUC':'V', 'GUG':'V', 'GUU':'V',\
'GCA':'A', 'GCC':'A', 'GCG':'A', 'GCU':'A','GAC':'D', 'GAU':'D',\
'GAA':'E', 'GAG':'E','GGA':'G', 'GGC':'G', 'GGG':'G', 'GGU':'G',\
'UCA':'S', 'UCC':'S', 'UCG':'S', 'UCU':'S','UUC':'F', 'UUU':'F',\
'UUA':'L', 'UUG':'L','UAC':'Y', 'UAU':'Y', 'UAA':'stop', \
'UAG':'stop','UGC':'C', 'UGU':'C', 'UGA':'stop', 'UGG':'W'}
triplet = 'AUG'
print(conversion[triplet])
def translate(codingRNAlist: list) -> str:
#conversion =
protein = '' # Initialise an empty protein
# Your code here
Mutation
Mutations can throw a spanner in the works with regard to protein functionality. For the purpose of this exercise, we will distinguish the following types of mutations:
Silent: mutation outside coding RNA.
Synonymous: no different amino acid sequence despite mutation in coding RNA.
Missense: single substitution in the amino acid sequence.
Nonsense: a sense codon is mutated into a stop codon, leading to early termination.
Resense: a stop codon is mutated into a sense codon, leading to extension of the protein.
Indel: alteration of reading frame by insertion or deletion (hence indel), often leading to a frameshift.
Exercise D: Mutation checker
Write a function mutationcheck that takes two DNA sequences and checks what
type of mutation occurs (if any). Possible outputs are: 'none', 'silent',
'synonymous', 'missense', 'nonsense' and 'resense'. You may assume that
there is only one mutated nucleotide and there are no indels. Your code should
be able to handle mutations that lead to the lack of a stop codon.
Example inputs:
'TTGTGATATAGGTACCAGTCACGTTGACGTAGTCTAGCTAGCATGTCAAGCACTTGAA','TTGTGATATAGGTACCAGTCACGTTGACGTAGTCTAGCTAGCATGTCTAGCACTTGAA'Example output:
'synonymous'
def mutationcheck(DNA_wildtype: str, DNA_mutation: str) -> str:
# Your code here
Point mutations in real life: Hemoglobin
In this exercise, you will apply the previously written functions to real genomic data.
Red blood cells are the body’s oxygen transporters. They contain an oxygen-binding protein called hemoglobin (Hb), which consists of four subunits. In adults, the most common form of Hb is hemoglobin A (HbA). It consists of two alpha and two beta globin subunits. The alpha globin subunit comes in two flavours: type 1 and type 2. You are given the DNA of healthy alpha 1, alpha 2, and beta globin.
alpha1globin = 'TATACTGGCGCGCTCGCGGGCCGGCACTCTTCTGGTCCCCACAGACTCAGAGAGAACCCACCATG'\
+ 'GTGCTGTCTCCTGCCGACAAGACCAACGTCAAGGCCGCCTGGGGTAAGGTCGGCGCGCACGCTGGCGAGTATGGTGC'\
+ 'GGAGGCCCTGGAGAGGATGTTCCTGTCCTTCCCCACCACCAAGACCTACTTCCCGCACTTCGACCTGAGCCACGGCT'\
+ 'CTGCCCAGGTTAAGGGCCACGGCAAGAAGGTGGCCGACGCGCTGACCAACGCCGTGGCGCACGTGGACGACATGCCC'\
+ 'AACGCGCTGTCCGCCCTGAGCGACCTGCACGCGCACAAGCTTCGGGTGGACCCGGTCAACTTCAAGCTCCTAAGCCA'\
+ 'CTGCCTGCTGGTGACCCTGGCCGCCCACCTCCCCGCCGAGTTCACCCCTGCGGTGCACGCCTCCCTGGACAAGTTCC'\
+ 'TGGCTTCTGTGAGCACCGTGCTGACCTCCAAATACCGTTAAGCTGGAGCCTCGGTGGCCATGCTTCTTGCCCCTTGG'\
+ 'GCCTCCCCCCAGCCCCTCCTCCCCTTCCTGCACCCGTACCCCCGTGGTCTTTGAATAAAGTCTGAGTGGGCGGCA'
alpha2globin = 'TATACTGGCGCGCTCGCGGCCCGGCACTCTTCTGGTCCCCACAGACTCAGAGAGAACCCACCATG'\
+ 'GTGCTGTCTCCTGCCGACAAGACCAACGTCAAGGCCGCCTGGGGTAAGGTCGGCGCGCACGCTGGCGAGTATGGTGC'\
+ 'GGAGGCCCTGGAGAGGATGTTCCTGTCCTTCCCCACCACCAAGACCTACTTCCCGCACTTCGACCTGAGCCACGGCT'\
+ 'CTGCCCAGGTTAAGGGCCACGGCAAGAAGGTGGCCGACGCGCTGACCAACGCCGTGGCGCACGTGGACGACATGCCC'\
+ 'AACGCGCTGTCCGCCCTGAGCGACCTGCACGCGCACAAGCTTCGGGTGGACCCGGTCAACTTCAAGCTCCTAAGCCA'\
+ 'CTGCCTGCTGGTGACCCTGGCCGCCCACCTCCCCGCCGAGTTCACCCCTGCGGTGCACGCCTCCCTGGACAAGTTCC'\
+ 'TGGCTTCTGTGAGCACCGTGCTGACCTCCAAATACCGTTAAGCTGGAGCCTCGGTAGCCGTTCCTCCTGCCCGCTGG'\
+ 'GCCTCCCAACGGGCCCTCCTCCCCTCCTTGCACCGGCCCTTCCTGGTCTTTGAATAAAGTCTGAGTGGGCAGCA'
betaglobin = 'TATAGGGCAGAGCCATCTATTGCTTACATTTGCTTCTGACACAACTGTGTTCACTAGCAACCTCAAA'\
+ 'CAGACACCATGGTGCATCTGACTCCTGAGGAGAAGTCTGCCGTTACTGCCCTGTGGGGCAAGGTGAACGTGGATGAA'\
+ 'GTTGGTGGTGAGGCCCTGGGCAGGCTGCTGGTGGTCTACCCTTGGACCCAGAGGTTCTTTGAGTCCTTTGGGGATCT'\
+ 'GTCCACTCCTGATGCTGTTATGGGCAACCCTAAGGTGAAGGCTCATGGCAAGAAAGTGCTCGGTGCCTTTAGTGATG'\
+ 'GCCTGGCTCACCTGGACAACCTCAAGGGCACCTTTGCCACACTGAGTGAGCTGCACTGTGACAAGCTGCACGTGGAT'\
+ 'CCTGAGAACTTCAGGCTCCTGGGCAACGTGCTGGTCTGTGTGCTGGCCCATCACTTTGGCAAAGAATTCACCCCACC'\
+ 'AGTGCAGGCTGCCTATCAGAAAGTGGTGGCTGGTGTGGCTAATGCCCTGGCCCACAAGTATCACTAAGCTCGCTTTC'\
+ 'TTGCTGTCCAATTTCTATTAAAGGTTCCTTTGTTCCCTAAGTCCAACTACTAAACTGGGGGATATTATGAAGGGCCT'\
+ 'TGAGCATCTGGATTCTGCCTAATAAAAAACATTTATTTTCATTGCAA'
Note that we have edited the sequences slightly to make the exercise easier. For instance, we removed the introns. You can download the original sequences from NCBI: HBA1, HBA2, and HBB.
Below, the genomic sequences for a person who suffers episodes of acute generalised pain, fatigue and dactylitis are given. We suspect the patient has the sickle cell anaemia, a disease where a genetic defect leads to malformed hemoglobin (called HbS), which undergoes polymerisation and leads to typical sickle-shaped red blood cells.
alpha1globin_patient = 'TATACTGGCGCGCTCGCGGGCCGGCACTCTTCTGGTCCCCACAGACTCAGAGAGAAC'\
+ 'CCACCATGGTGCTGTCTCCTGCCGACAAGACCAACGTCAAGGCCGCCTGGGGTAAGGTCGGCGCGCACGCTGGCGAG'\
+ 'TATGGTGCGGAGGCCCTGGAGAGGATGTTCCTGTCCTTCCCCACCACCAAGACCTACTTCCCGCACTTCGACCTGAG'\
+ 'CCACGGCTCTGCCCAGGTTAAGGGCCACGGCAAGAAGGTGGCCGACGCGCTGACCAACGCCGTGGCGCACGTGGACG'\
+ 'ACATGCCCAACGCGCTGTCCGCCCTGAGCGACCTGCACGCGCACAAGCTTCGGGTGGACCCGGTCAACTTCAAGCTC'\
+ 'CTAAGCCACTGCCTGCTGGTGACCCTGGCCGCCCACCTCCCCGCCGAGTTCACCCCTGCGGTGCACGCCTCCCTGGA'\
+ 'CAAGTTCCTGGCTTCTGTGAGCACCGTGCTGACCTCCAAATACCGTTAAGCTGGAGCCTCGGTGGCCATGCTTCTTG'\
+ 'CCCCTTGGGCCTCCCCCCAGCCCCTCCTCCCCTTCCTGCACCCGTACCCCCGTGGTCTTTGAATAAAGTCTGAGTGG'\
+ 'GCGGCA'
alpha2globin_patient = 'TATACTGGCGCGCTCGCGGCCCGGCACTCTTCTGGTCCCCACAGACTCAGAGAGAAC'\
+ 'CCACCATGGTGCTGTCTCCTGCCGACAAGACCAACGTCAAGGCCGCCTGGGGTAAGGTCGGCGCGCACGCTGGCGAG'\
+ 'TATGGTGCGGAGGCCCTGGAGAGGATGTTCCTGTCCTTCCCCACCACCAAGACCTACTTCCCGCACTTCGACCTGAG'\
+ 'CCACGGCTCTGCCCAGGTTAAGGGCCACGGCAAGAAGGTGGCCGACGCGCTGACCAACGCCGTGGCGCACGTGGACG'\
+ 'ACATGCCCAACGCGCTGTCCGCCCTGAGCGACCTGCACGCGCACAAGCTTCGGGTGGACCCGGTCAACTTCAAGCTC'\
+ 'CTAAGCCACTGCCTGCTGGTGACCCTGGCCGCCCACCTCCCCGCCGAGTTCACCCCTGCGGTGCACGCCTCCCTGGA'\
+ 'CAAGTTCCTGGCTTCTGTGAGCACCGTGCTGACCTCCAAATACCGTTAAGCTGGAGCCTCGGTAGCCGTTCCTCCTG'\
+ 'CCCGCTGGGCCTCCCAACGGGCCCTCCTCCCCTCCTTGCACCGGCCCTTCCTGGTCTTTGAATAAAGTCTGAGTGGG'\
+ 'CAGCA'
betaglobin_patient = 'TATAGGGCAGAGCCATCTATTGCTTACATTTGCTTCTGACACAACTGTGTTCACTAGCA'\
+ 'ACCTCAAACAGACACCATGGTGCATCTGACTCCTGTGGAGAAGTCTGCCGTTACTGCCCTGTGGGGCAAGGTGAACG'\
+ 'TGGATGAAGTTGGTGGTGAGGCCCTGGGCAGGCTGCTGGTGGTCTACCCTTGGACCCAGAGGTTCTTTGAGTCCTTT'\
+ 'GGGGATCTGTCCACTCCTGATGCTGTTATGGGCAACCCTAAGGTGAAGGCTCATGGCAAGAAAGTGCTCGGTGCCTT'\
+ 'TAGTGATGGCCTGGCTCACCTGGACAACCTCAAGGGCACCTTTGCCACACTGAGTGAGCTGCACTGTGACAAGCTGC'\
+ 'ACGTGGATCCTGAGAACTTCAGGCTCCTGGGCAACGTGCTGGTCTGTGTGCTGGCCCATCACTTTGGCAAAGAATTC'\
+ 'ACCCCACCAGTGCAGGCTGCCTATCAGAAAGTGGTGGCTGGTGTGGCTAATGCCCTGGCCCACAAGTATCACTAAGC'\
+ 'TCGCTTTCTTGCTGTCCAATTTCTATTAAAGGTTCCTTTGTTCCCTAAGTCCAACTACTAAACTGGGGGATATTATG'\
+ 'AAGGGCCTTGAGCATCTGGATTCTGCCTAATAAAAAACATTTATTTTCATTGCAA'
Exercise E: Hemoglobin
Use your function mutationcheck() to find out what is wrong. Try to understand
how the for loop works and replace A, B and C in the code below with something
else. In which subunit of hemoglobin does the mutation occur?
# Complete the following code
paired_genes = [('alpha1', alpha1globin, alpha1globin_patient),
('alpha2', alpha2globin, alpha2globin_patient),
('beta', betaglobin, betaglobin_patient)]
# Replace A, B and C with the correct variables:
for A, B, C in paired_genes:
outcome = mutationcheck(healthygene,patientgene)
print("Mutation in " + genename + ": " + outcome)
Explain the outcome.
Exercise 8.20 ([***] Caesar’s cipher)
No doubt you will have seen the enciphering/deciphering methods with shifting the alphabet. For example, A becomes D, B becomes E, etc. This is something you can do in Python.
We start with a message, written in a string.
message = 'CAESARSDECIPHERING'
Have you ever heared of ASCII (American Standard Code for
Information Interchange)? Each character or string has a numerical ASCII value.
For A it is 65, for Z it is 95. To convert from ASCII to a string in Python, you use the chr() function, whose name originates from the word ‘character’.
The code below generates a variable Str, which holds the alphabet:
alphabet = np.arange(65,91)
Str = []
for ii in alphabet:
Str.append(chr(ii))
Str=''.join(Str)
print(Str)
In order to decipher our message, we need a variable Str_decipher, for
which the variable Str is shifted. In this case we use a shift (Caesar
number) of 2.
caesar_num = 2 # Between 0 and 25
Str_decipher = Str[caesar_num:] + Str[:caesar_num]
print(Str_decipher)
In order to encrypt, we need to:
go over each character in the string
find the location in the regular alphabet (
Str), withStr.index(character)find the corresponding character in the new alphabet (
Str_decipher)append that character to the encrypted message
new_message = []
for ii in message:
index = Str.index(ii) # Go over each character in the string
new_character = Str_decipher[index] # Find the location in the regular alphabet
new_message.append(new_character) # Extract the corresponding character in the new alphabet
new_message=''.join(new_message) # Stitches all characters in the array to one string
print(new_message)
Exercise A: Deciphering function
You have seen how to encrypt. The challenge is now to decrypt a message.
Let’s start by making code which takes as input the Caesar number and
message_to_decipher, and outputs the message_original.
Name your function Caesar_decipher.
message = 'EGCUCTUFGEKRJGTKPI'
caesar_num = 2
def Caesar_decipher(message,caesar_num):
# Your code here
Exercise B: Caesar number
Can you decipher without the value of the Caesar number given?
message_to_decipher = 'KVCQOBFSORKWHVCIHGDOQSG'
# Your code here
Exercise 8.21 ([**] DNA sequence analysis)
Write a function that takes a DNA sequence (a string of characters A, T, C, G) and returns a dictionary with the counts of each nucleotide.
Handle invalid characters by ignoring them.
Provide an option to return the counts as a percentage of the total number of nucleotides.
Example output:
dna_count("ATCGATCGAATCGA") # Returns {'A': 5, 'T': 3, 'C': 4, 'G': 3}
dna_count("ATCGATCGAATCGA", percent=True) # Returns {'A': 35.7, 'T': 21.4, 'C': 28.6, 'G': 21.4}
# Your code here
Exercise 8.22 ([***] Fibonacci sequence)
Write a recursive function that generates the Fibonacci sequence up to a given number \(n\) and returns a list containing the Fibonacci numbers. The Fibonacci sequence is defined as:
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) for n > 1
Example output:
fibonacci_up_to(10) # Returns [0, 1, 1, 2, 3, 5, 8]
# Your code here
Exercise 8.23 ([***] Prime factorization)
Write a function that computes the prime factorization of a given integer \(n\). The function should return the prime factors in a list. Ensure that the function works for any integer greater than 1.
Example output:
prime_factors(28) # Returns [2, 2, 7]
# Your code here
Exercise 8.24 ([***] Matrix multiplication)
Implement a function that multiplies two matrices. The function should handle matrices of different sizes and return the resulting matrix.
Ensure the matrices can be multiplied (i.e., the number of columns in the first matrix must equal the number of rows in the second matrix).
Raise an error if the multiplication cannot be performed.
Note: functions for this already exist in NumPy, but try to come up with your own.
# Your code here