Problems

1. Consider a radiating time-harmonic point source in \(\mathbf{r}_1=(x_1,0,0)\). The complex field in the point of observation \(\mathbf{r}=(x,y,z)\), where \(z>0\), is given by:

\[\begin{align*} U_1(x,y,z) = Q_1 \frac{e^{ik \sqrt{(x-x_1)^2 + y^2 + z^2}}}{\sqrt{(x-x_1)^2 + y^2 + z^2}}. \end{align*}\]

where \(Q_1\) is a given complex number of which the modulus is proportional to the source strength.

• a) Derive that for fixed \(z_1\) and for sufficiently large \(z>0\) the field can be approximated by

(435)\[\begin{align*} U_{1,far}(x,y,z) = Q_1 \frac{e^{ik z}}{z} e^{i k\frac{x^2+ y^2}{2z}} e^{-i \frac{k x_1 x}{z}}. \end{align*}\]

• b) Let there be a second point source at \(\mathbf{r}_2=(x_2,0,0)\), with complex source strength \(Q_2\) with \(|Q_2|=|Q_1|\). We assume that both point sources are coherent. This means that there is \(\phi\) such that \(Q_2=Q_1 e^{i \phi}\). Show that the field in \((x,y,z)\) for \(z>0\) large due to the two point sources can be written as

(436)\[\begin{align*} U(x,y,z) \approx U_{1,far}(x,y,z)\left( 1 + e^{i\phi} e^{i \frac{k \Delta x x}{z}} \right), \end{align*}\]

where \(\Delta x = x_1-x_2\).

• c) For which angles \(\theta=x/z\) does the intensity in far field vanish? Show that the distance between the point sources \(\Delta x\) can be determined from the angular separation of the zeros of the intensity. Does the angular separation depend on the phase difference \(\phi\)?

• d) What should be the phase difference between the point sources such that for \(x/z=0\) on the screen at large distance \(z\) the intensity vanishes?

2. Consider two slits of equal width \(a\) in a non-transparent screen of thickness \(d\) in the plane \(z=0\) as shown in Fig. 108. The screen is illuminated by a plane wave with unit amplitude and propagating in the positive \(z\)-direction. In the second slit there is a piece of glass with refractive index \(n\) and thickness \(d\). In the first slit there is vacuum.

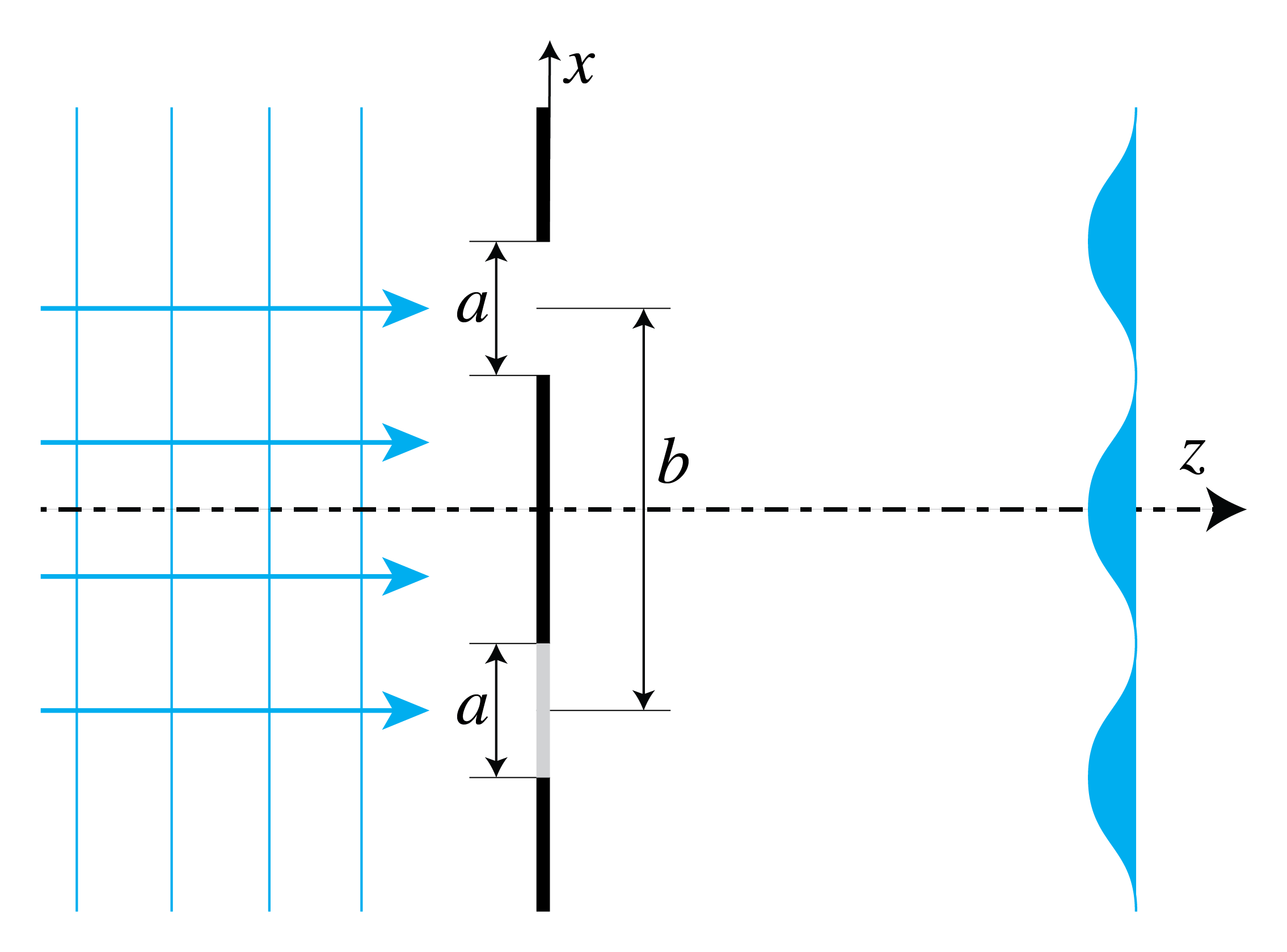
Fig. 108 Two slits centred at \(y=0\) and very long in the \(y\)-direction in a dark screen of thickness \(d\). The lower slit is filled with glass, the upper is in vacuum.

• a) If the field immediately behind slit 1 has complex amplitude equal to \(1\), explain that the field immediately after behind 2 is given by

\[\begin{align*} e^{ i \phi} \end{align*}\]

with \(\phi= k (n-1)d\).

• b) Derive (using (435) or in another way) that the Fraunhofer intensity pattern on a screen along the line \(y=0\) at large distance \(z\) is given by (upto factors that do not depend on \(x/z\)).

(437)\[\begin{align*} I_{far}(x,0,z) = 2 \frac{a^2}{z^2} \left[ \frac{\sin \left(\frac{kax}{2z}\right)}{\frac{kax}{2z}}\right]^2 \left[ 1 + \cos\left( \frac{k b x}{z} +\phi\right)\right]. \end{align*}\]

In deriving this result you may omit all factors that are independent of \(x/z\). 5and \(y/z\). If you use (436) you may take \(Q_1=1\), \(Q_2=e^{i \phi}\).

• c) Make a sketch of this intensity pattern, showing the zeros and maxima as function of \(\theta=x/z\) when \(a=2 \lambda\), \(b=4 \lambda\) and \(\phi=-\pi/2\). Explain where the the envelope and the other factor that depends on \(x/z\) are caused by.

3. We consider the optical set-up shown at the left of Fig. 109 where a point source at point \(\mathbf{r}_s=(a, 0,0)\) is above a plane mirror in the plane \(x=0\). The time-harmonic field emitted by the point source without the mirror being present is in complex notation given by:

\[\begin{align*} U_s(x,y,z,t)= \frac{e^{i k \sqrt{ (x-a)^2 + y^2 + z^2}-i \omega t}}{\sqrt{(x-a)^2 + y^2 + z^2}}. \end{align*}\]

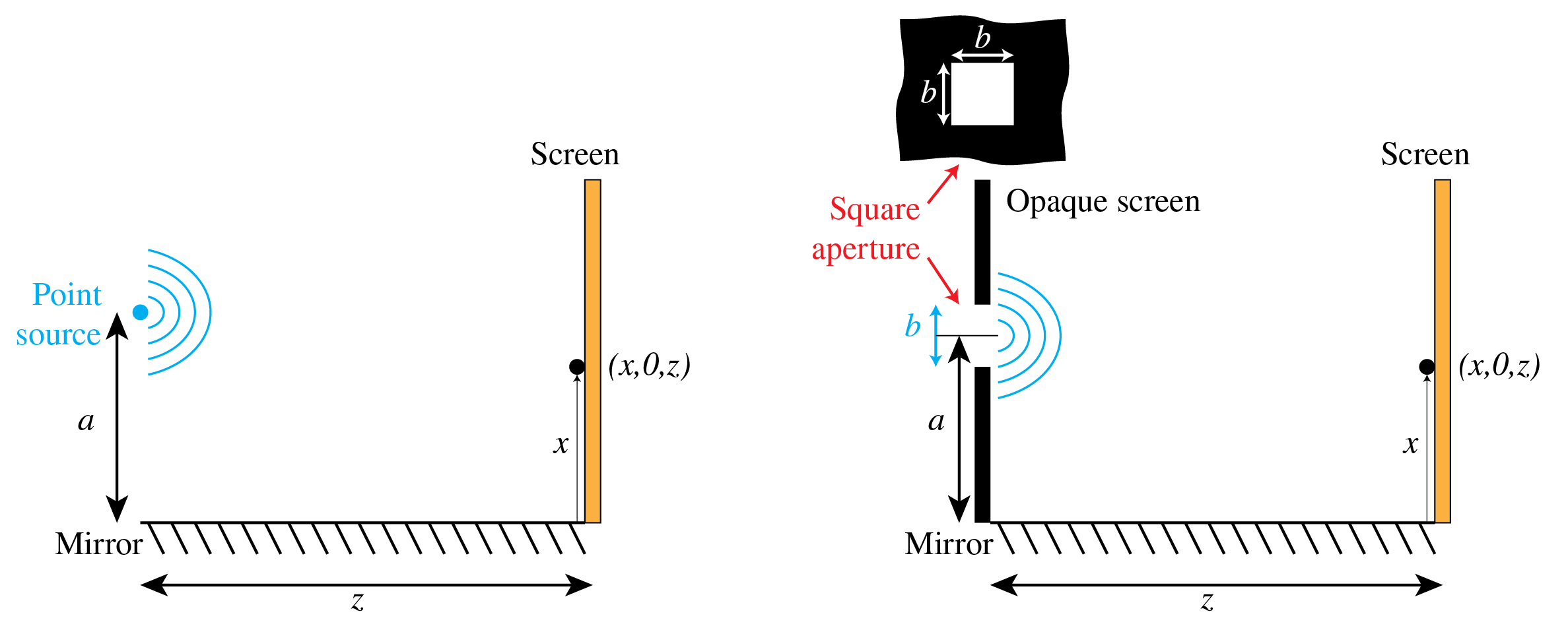
Fig. 109 Lloyd mirror configuration with a point source (left) and a rectangular aperture in a dark screen (right), above a mirror and with a screen at distance \(z\) where the field is observed.

• a) Let \(U_r\) be the field reflected by the mirror. Assume that the mirror is perfect so that the total field \(U_s(x,y,z)+U_r(x,y,z)\) is zero on the surface of the mirror, i.e. when \(x=0\). Show that the reflected field \(U_r\) can be considered to be emitted by a point source in \((-a,0,0)\), which is the image of the original point source by the mirror, and which is out of phase with the original point source and has the same strength.

• b) Consider the field on a screen at \(z>0\). According to (a) the field in the presence of the mirror can be considered to be radiated by two point sources, namely at \((a,0,0)\) and \((-a,0,0)\), that are of equal strength and out of phase with each other. Assume that \(z\) is so large that the spherical waves emitted by these point sources and arriving at the screen can both be considered to be plane waves. Derive that the point on the screen \((x,0,z)\) with smallest \(x>0\) where the field is zero is given by

(438)\[\begin{align*} x= \frac{\lambda}{2a} z, \end{align*}\]

where \(\lambda\) is the wavelength. In your derivation use path length differences of interfering rays and make a drawing.

• c) What happens with this zero and with the fringe patten on the screen when the perfect mirror is replaced by a dielectric such as a piece of glass?

• d) Suppose now that there is a second point source at \((2a,0,0)\) above the mirror and suppose that it has the same strength and is in phase with the point source in \((a,0,0)\). Assume again that the mirror is perfectly reflecting and derive (again by considering path length differences and using a drawing) that the smallest \(x>0\) for which a zero occurs in point \((x,0,z)\) on the screen is given by

\[\begin{align*} x= \frac{\lambda}{3a}z \end{align*}\]

• e) Derive the smallest \(x>0\) for which the field is zero in \((x,0,z)\) when the two point sources at \((a,0,0)\) and \((2a,0,0)\) are mutually incoherent. Use again path length differences and make a drawing.

• f) Next suppose that there is a square aperture with centre at \((a,0,0)\) and sides of length \(b<a\) parallel to the \(x\)- and \(y\)-directions in an opaque (i.e. dark) screen above the mirror as shown at the right of Fig. 109. The aperture is illuminated by a plane wave that propagates parallel to the \(z\)-axis, hence the field in the aperture has constant phase and amplitude. Compute the smallest positive \(x\) for which a zero occurs at \((x,0,z)\) on the screen at large distance \(z>0\). Use again path length differences and a drawing in your derivation.

4. Note: to answer the following questions it is NOT necessary to compute diffraction integrals.

• a) Consider two equally strong point sources which with respect to a coordinate system \((x,y,z)\) are at \((-a/2,0,0)\) and \((a/2,0,0)\), where the \(z\)-axis is the optical axis. Suppose the point sources are mutually coherent and suppose that they emit in phase. The maximum intensity on a screen at large (i.e. Fraunhofer) distance is then on the optical axis. Show that the smallest angle with the optical axis at which there is a zero on this screen is given by \(\lambda/(2a)\).

• b) What is the smallest angle with the optical axis at which there is a zero on the screen when the two point sources emit with phase difference \(\pi/2\)?

• c) Are there any zeros on the screen when the two point sources are mutually incoherent?

• d) Consider now two identical apertures in an opaque screen at \(z=0\). One aperture has its centre at \((-a/2,0,0)\) and the other has its centre at \((a/2,0,0)\). The apertures are illuminated by a time-harmonic plane wave at perpendicular incidence to the screen (i.e. propagating parallel to the \(z\)-axis). Explain that whatever the shape of these apertures, the smallest angle for which a zero occurs in the far field intensity is at \(\lambda/(2a)\).

• e) Suppose that the plane wave is incident at some angle different from \(90^o\). Let its complex field be given by

\[\begin{align*} U(x,z)= e^{i (k_x x + k_z z)} \end{align*}\]

where \(\sqrt{k_x^2+k_z^2}=k\). Suppose that \(k_x a =\pi/2\) (modulo \(2\pi\)). What is now the smallest angle where a zero occurs on the screen in far field? Explain your answer.

• f) Now imagine that both (identical) apertures are filled with glass plates with thickness that varies with position. The two glass plates are identical and they are identically positioned in each of the two apertures. Imagine that we illuminate the apertures with a plane wave at perpendicular incidence. The field transmitted by each aperture is now a rather complicated function of position, however the transmitted fields behind both apertures are identical. Does the far field intensity still vanish for angle \(\lambda/(2a)\) or will it be modified by the presence of the glass plates? Explain your answer.

5. Bessel beams.

Suppose there is a mask in the entrance pupil of radius \(a\) of a positive thin lens with image focal length \(f_i\) with a thin ring-shaped aperture at \(r=b\) with width \(\Delta r\). If a plane wave with amplitude \(A\) is at perpendicular incidence on the mask, the field immediately behind the mask is given by

\[\begin{split}\begin{align*} U_{Bessel}(x,y)= \left\{ \begin{array}{l}A, \;\;\; \text{ if } b-\Delta r < \sqrt{x^2+y^2}<b, \\0, \;\;\; \text{ otherwise} \end{array}\right. \end{align*}\end{split}\]

• a) Use the integral

\[\begin{align*} \int_0^{2\pi} e^{i \zeta \cos \psi} \mathrm{d}\psi = 2\pi J_0(\zeta). \end{align*}\]

to derive that for sufficiently small \(\Delta r\), the field in the focal plane is in good approximation given by

\[\begin{align*} U_{Bessel}(x,y,f_i)= 2\pi A b \Delta r J_0\left( k \frac{b r}{f}\right). \end{align*}\]

• b) The beam obtained this way is called a Bessel beam. Explain why this beam has a very long focal depth.

• c) Suppose that the Airy spot obtained by focussing of a unit amplitude plane wave and the Bessel beam carry the same amount of energy. Show that then the amplitude of the Bessel beam is given by

\[\begin{align*} A = \frac{a}{\sqrt{2 b \Delta r}} \end{align*}\]

• d) Derive that the ratio of the field amplitudes in the focal point of the Bessel beam i: \(U_{Bessel}(0,0,f_i)\) and the Airy spot: \(U_{Airy}(0,0,f_i)\) is given by

\[\begin{align*} \frac{U_{Bessel}}{U_{Airy}} = \frac{\sqrt{2 b \Delta r}}{ a}. \end{align*}\]

If \(b=a\) and \(\Delta r=0.1 a\) this becomes

\[\begin{align*} \frac{U_{Bessel }}{U_{Airy}} = \sqrt{\frac{2 \Delta r}{ a}} \approx 0.44, \end{align*}\]

which is the case shown in Fig. 110.

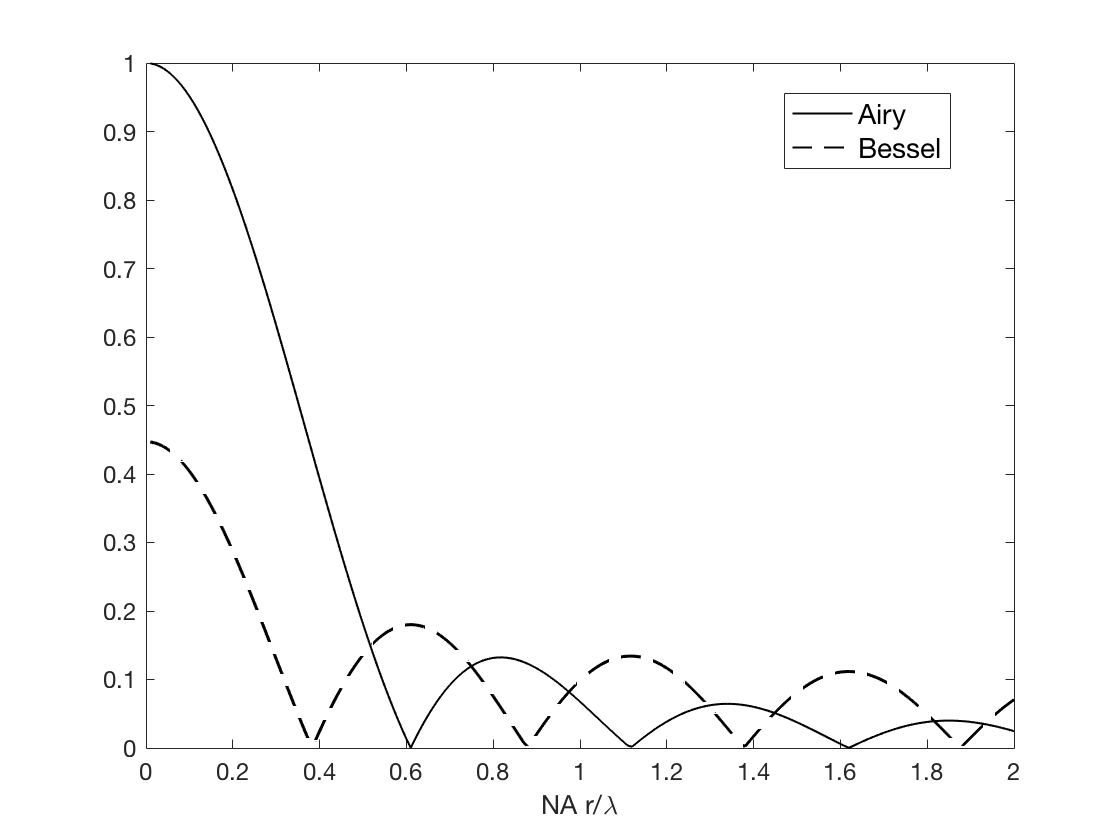
Fig. 110 Amplitude in the focal plane of a Bessel beam and of an Airy spot with the same total energy. The lens pupil has diameter \(a=10000 \lambda\), the ring aperture of the Bessel beam case is at the outer edge of the pupil (\(b=a\)) and has width \(\Delta r = 0.1 a\) and the \(\text{NA}=0.1\).

• e) The Bessel beam has stronger side lobes than the Airy spot. Explain the reason.

6. * Stellar interferometry.

We consider the emission by a star of light of a narrow frequency band with centre frequency \(\mathbf{a}r{\omega}\) and corresponding wavelength \(\mathbf{a}r{\lambda}=c 2\pi/\mathbf{a}r{\omega}\) The star is an extended spatially incoherent source. Let \(I(x,y)\) be the intensity on the star’s surface orientated towards the earth. The aim of the exercise is to determine \(I(x,y)\) by stellar interferometry.

Let \(U_0(x,y,t)\) be the field emitted at the surface of the star. Then the mutual coherence function at points \(S_1=(x_1,y_1)\), \(S_2=(x_2, y_2)\) on the surface of the star is:

\[\begin{split}\begin{align*} \Gamma(S_1,S_2, \tau)&= \braket{ U_0(S_1,t)^* U_0(S_2,t+\tau)} \\ &= I(x_1,y_1) e^{i \omega \tau} \delta(x_1- x_2)\delta(y_1- y_2) \;\;\; \text{ for all } \tau. \end{align*}\end{split}\]

• a) Let \(z_e\) be the distance of the star from earth. Use the quasi-monochromatic approximation to derive the field in a point \(P_e=(x_e,y_e)\) on earth.

• b) Show that the mutual coherence function in two points \(P_e=(x_e,y_e)\) and \(\tilde{P}_2=(\tilde{x}_e, \tilde{y}_e)\) on earth is for \(\tau=0\) given by

\[\begin{align*} \Gamma(P_e, \tilde{P}_e,\tau=0) = \int\int I(x_1,y_1) e^{2\pi i \left( \frac{x_e - \tilde{x}_e }{\mathbf{a}r{\lambda} z_e} x_1 + \frac{y_e -\tilde{y}_e }{\mathbf{a}r{\lambda} z_e}y_1\right) } \, dx_1 dy_1. \end{align*}\]

i.e. the mutual coherence function between points on earth for time delay \(\tau=0\) can be expressed in the Fourier transform of the intensity \(I(x,y)\) emitted by the star, evaluated at spatial frequencies \(\xi=\frac{x_e - \tilde{x}_e }{\mathbf{a}r{\lambda} z_e} \) and \(\eta=\frac{y_e -\tilde{y}_e }{\mathbf{a}r{\lambda} z_e}\).

• c) Explain how the mutual coherence for time delay \(\tau=0\) can be measured on earth using interferometry and how this can lead to retrieving the intensity of the star.

• d) What determines the resolution that can be achieved?