Problems

1. Principle of Fermat and Snell’s Law.

Consider a layer of thickness \(d\) and refractive index \(n_2\) which is sandwiched between two half spaces with refractive index \(n_1\) and \(n_3\) as shown in Fig. 39. A ray from point \(P=(x_P,y_P)\) with \(y_P>d\) passes through point \(Q=(x_Q,y_Q)\) with \(y_Q<0\).

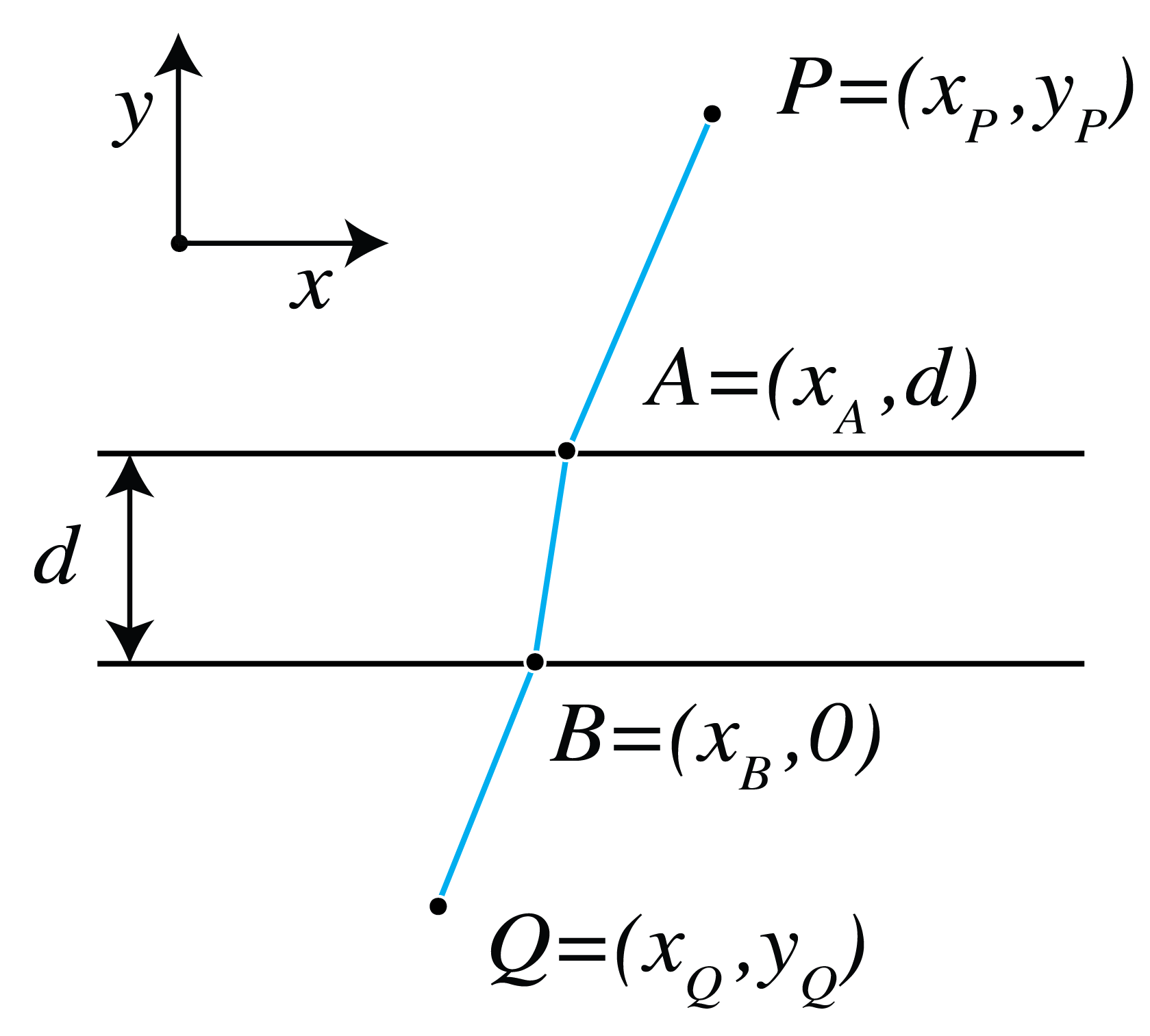
Fig. 39 A ray through points \(P\) and \(Q\).

• a) Write a formula for the OPL of the ray from \(P\) to \(Q\) as shown in Fig. 39.

• b) Find the equations to be satisfied by \(x_A\) and \(x_B\) such that the OPL is minimum. Hint: set the partial derivatives of the OPL with respect to \(x_A\) and \(x_B\) equal to zero.

• c) Express the equations derived under b) in terms of \(\sin \theta_1\), \(\sin \theta_2\) and \(\sin \theta_3\) and derive that Snell’s Law holds for the angles \(\theta_1\) and \(\theta_3\):

(241)\[\begin{align*} n_1 \sin \theta_1 = n_3 \sin \theta_3. \end{align*}\]

Note that the relationship between \(\theta_3\) and \(\theta_1\) is independent of the refractive index \(n_2\) and the thickness \(d\) of the middle layer.

• d) Does Snell’s Law (241)) hold irrespective of the number of layers and their thicknesses in between the two half spaces? Explain your answer.

• e) Derive (241) by using the boundary conditions for the tangential components of the electromagnetic field, as described in Maxwell Boundary Conditions.

2. Perfect focusing by an ellipsoid and a hyperboloid.

Suppose that there are two media with refractive indices \(n_1>n_2\) and that point \(S\) is at infinity in the medium with refractive index \(n_2\). We will construct a surface (interface) between the two media such that all rays from \(S\) are focused into the same point \(F\) (see Fig. 40a). Because \(S\) is at very large distance, the rays entering from the right are parallel. Since all parallel rays have travelled the same distance when they hit the surface \(DD'\) perpendicular to the rays, all parallel rays have the same phase at their intersection points with the plane \(DD'\).

• a) If point \(A\) is on the interface sought, derive that

(242)\[\begin{align*} \frac{n_2}{c} |DA| + \frac{n_1}{c}|AF| = \text{constant}, \end{align*}\]

the constant is the same for all points \(A\) on the interface.

• b) Show that by moving the plane \(DD'\) parallel to itself we can achieve that for the new plane \(DD'\) we get:

• c) Suppose next that \(n_2>n_1\). as shown at the right of Fig. 40. Show that now, by the same argument as above, the interface is a hyperboloid with \(F\) as one of its focal points.

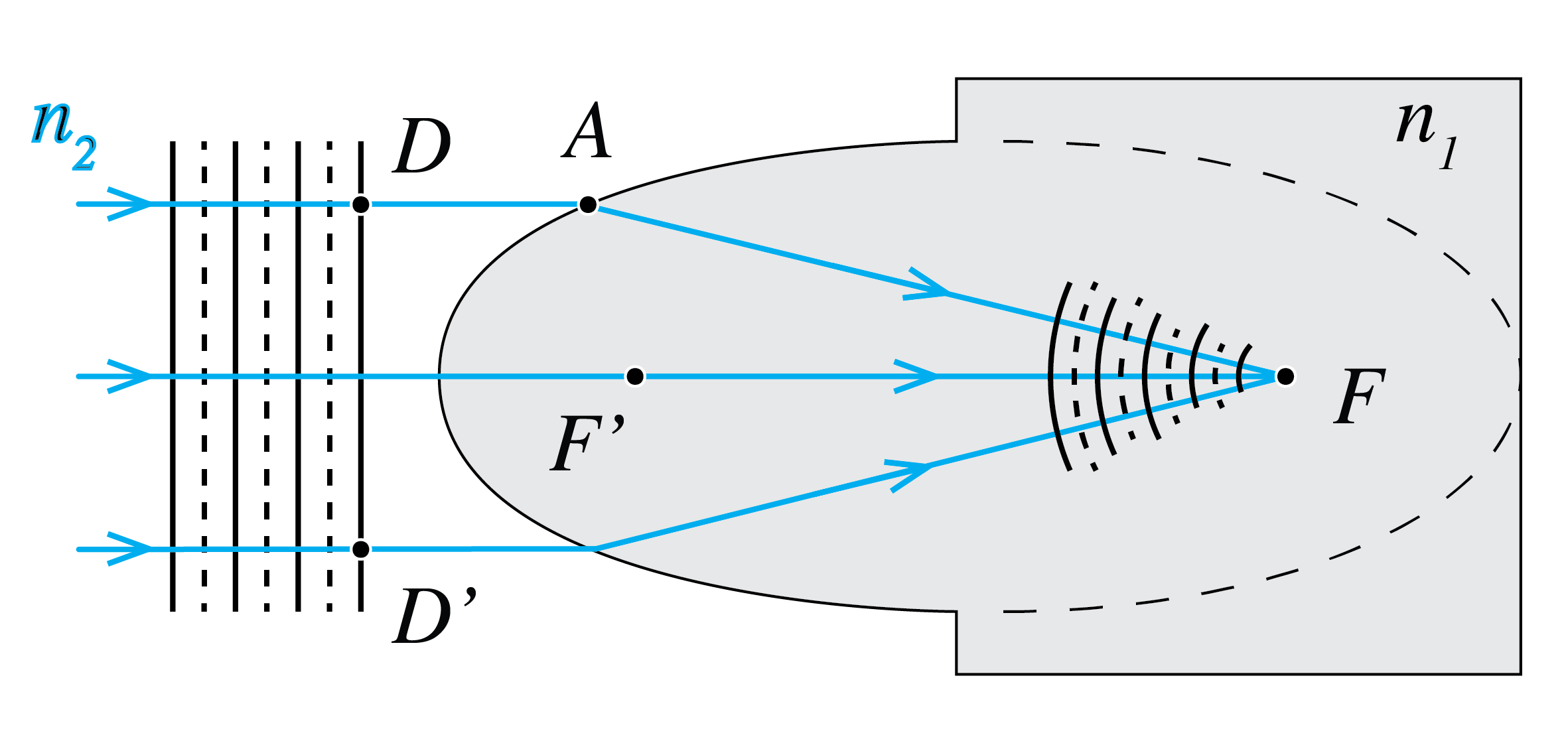
Fig. 40 (a) Ellipsoid (\(n_2<n_1\)) and (b) hyperboloid (\(n_2>n_1\)) to perfectly focus a parallel beam incident from the medium with refractive index \(n_2\) into a point in a medium with refractive index \(n_1\).

• d) Use the previous results to describe a lens with refractive index \(n_2>n_1\) and having hyperboloid surfaces which perfectly images two given points S and P in the ambient medium with refractive index \(n_1\).

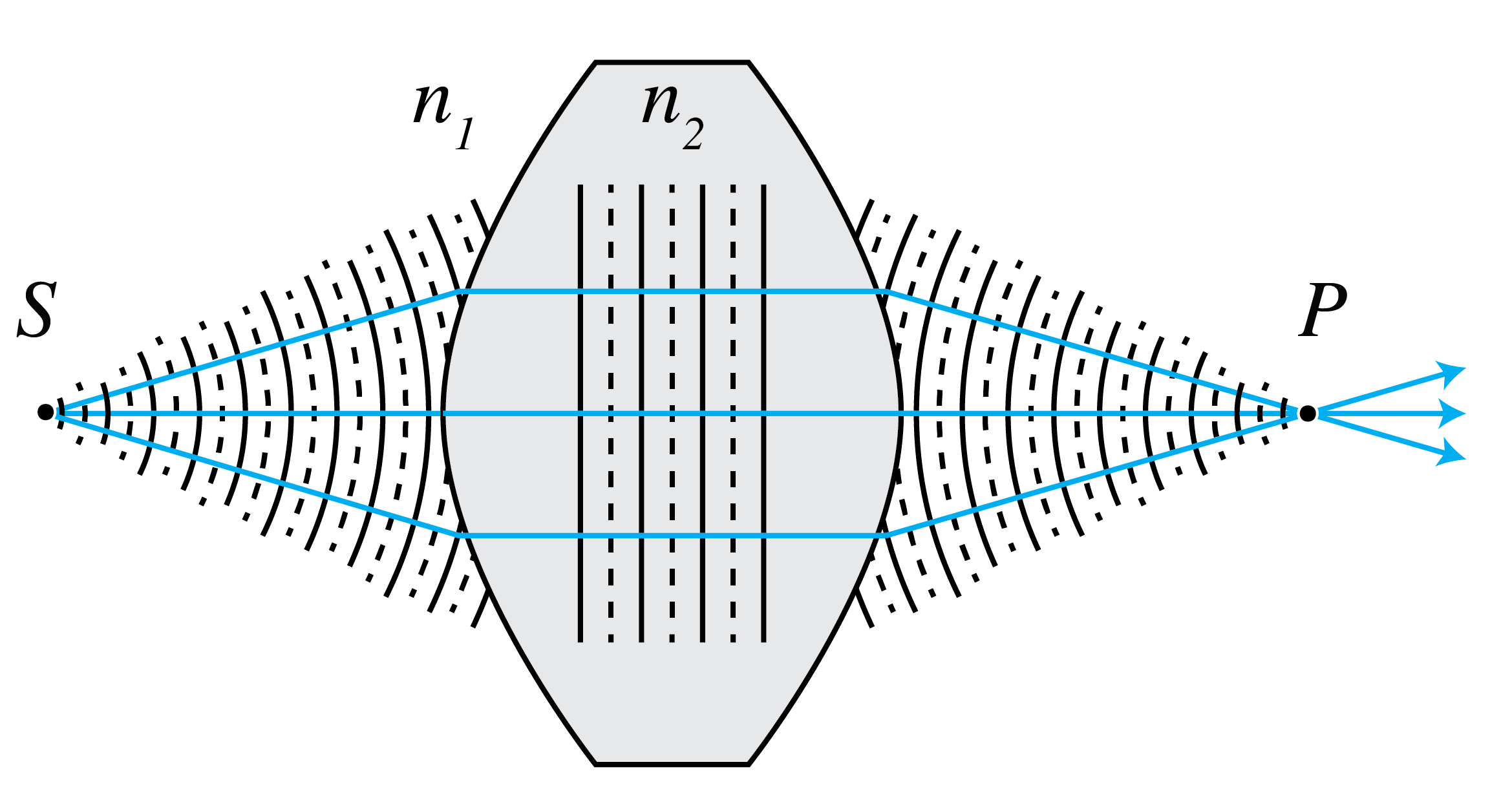
Fig. 41 Lens with hyperboloid surfaces for perfect imaging of a pair of points.

3. Perfect focussing by a parabolic mirror

Next we consider perfect focusing of parallel rays in air (\(n=1\)) by a mirror. Let there be a parallel bundle of rays in air (\(n=1\)) and suppose we want to focus all rays in point \(F\).

• a) We draw a plane \(\Sigma_1\) perpendicular to the rays as shown in Fig. 42. The rays that hit \(\Sigma_1\) have traversed the same optical path length. Draw a second surface \(\Sigma_2\) parallel to \(\Sigma_1\). Consider rays hitting the mirror in \(A_1\) and \(A_2\). Derive that

(243)\[\begin{align*} \text{OPL}=|W_1A_1| + |A_1F|= |W_2A_2| + |A_2F|. \end{align*}\]

• b) Derive that

(244)\[\begin{align*} |W_1A_1| + |A_1D_1|= |W_2A_2| + |A_2D_2|. \end{align*}\]

• c) Show that (243) is satisfied for points \(A\) for which \(|AF|=|AD|\), and conclude that the mirror is a paraboloid with \(f\) as focus and \(\Sigma_2\) as diretrix.

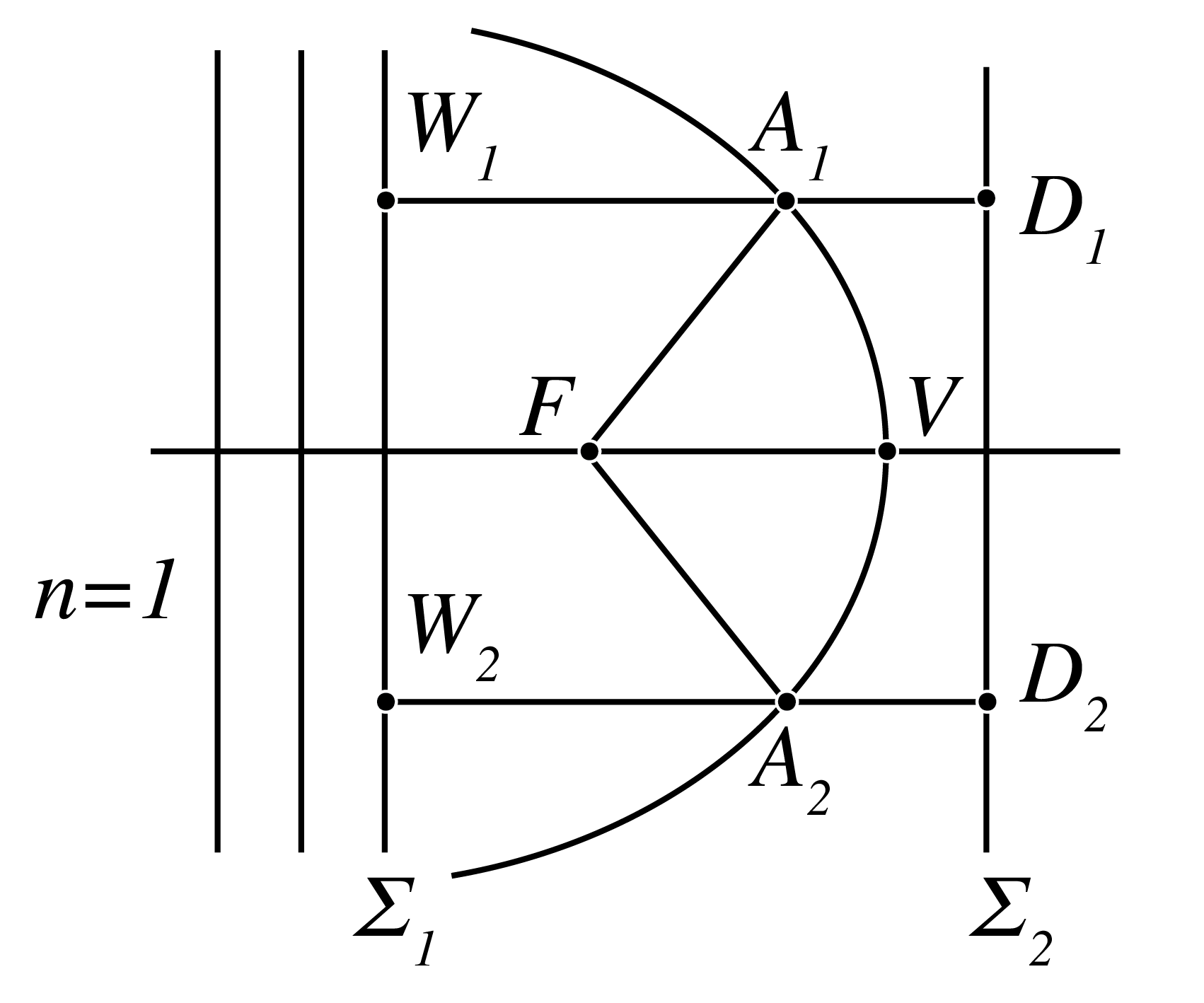
Fig. 42 A paraboloid mirror.

4. Imaging of a virtual object.

A virtual object is at a distance \(d_0\) behind a converging lens. The converging incident rays to the left of the lens, that correspond to the virtual object, are shown in Fig. 43. The lens has focal length \(f\).

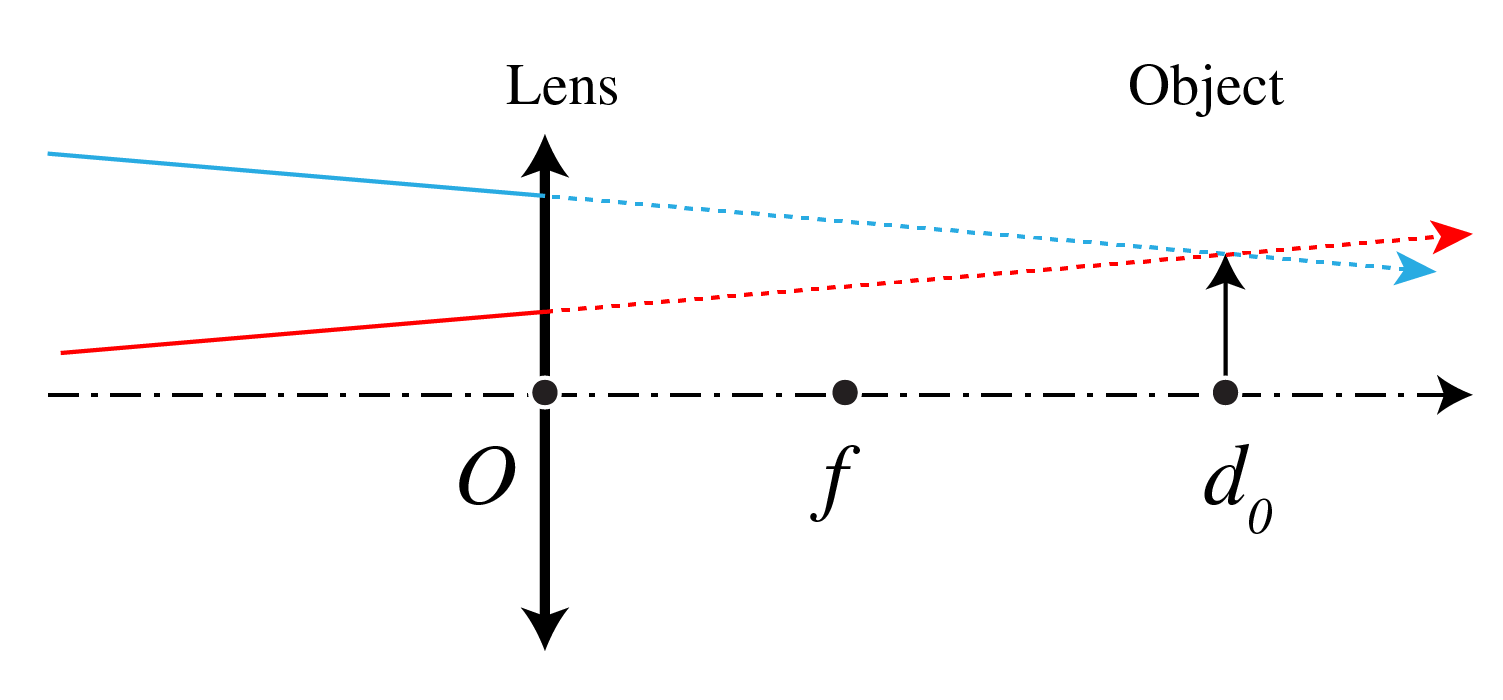
Fig. 43 An object is created by incoming rays.

• a) Construct the image when \(f=2\) cm, \(d_0=4\) cm and the height of the object 1 cm.

• b) Is the image real or virtual? Inverted or upright?

• c) Calculate the location of the image using the lens formula and compare it with your drawing. What is the magnification?

5. Suppose we have two thin lenses \({\cal L}_1\) and \({\cal L}_2\). Lens \({\cal L}_1\) is convergent (i.e. positive) with focal distance \(f_1>0 \) and lens \({\cal L}_2\) is divergent (i.e. negative) with focal distance \(f_2<0\). The distance between the lenses is \(d\). Let there be an object at distance \(2f_1\) in front of lens \({\cal L}_1\), as shown in Fig. 44.

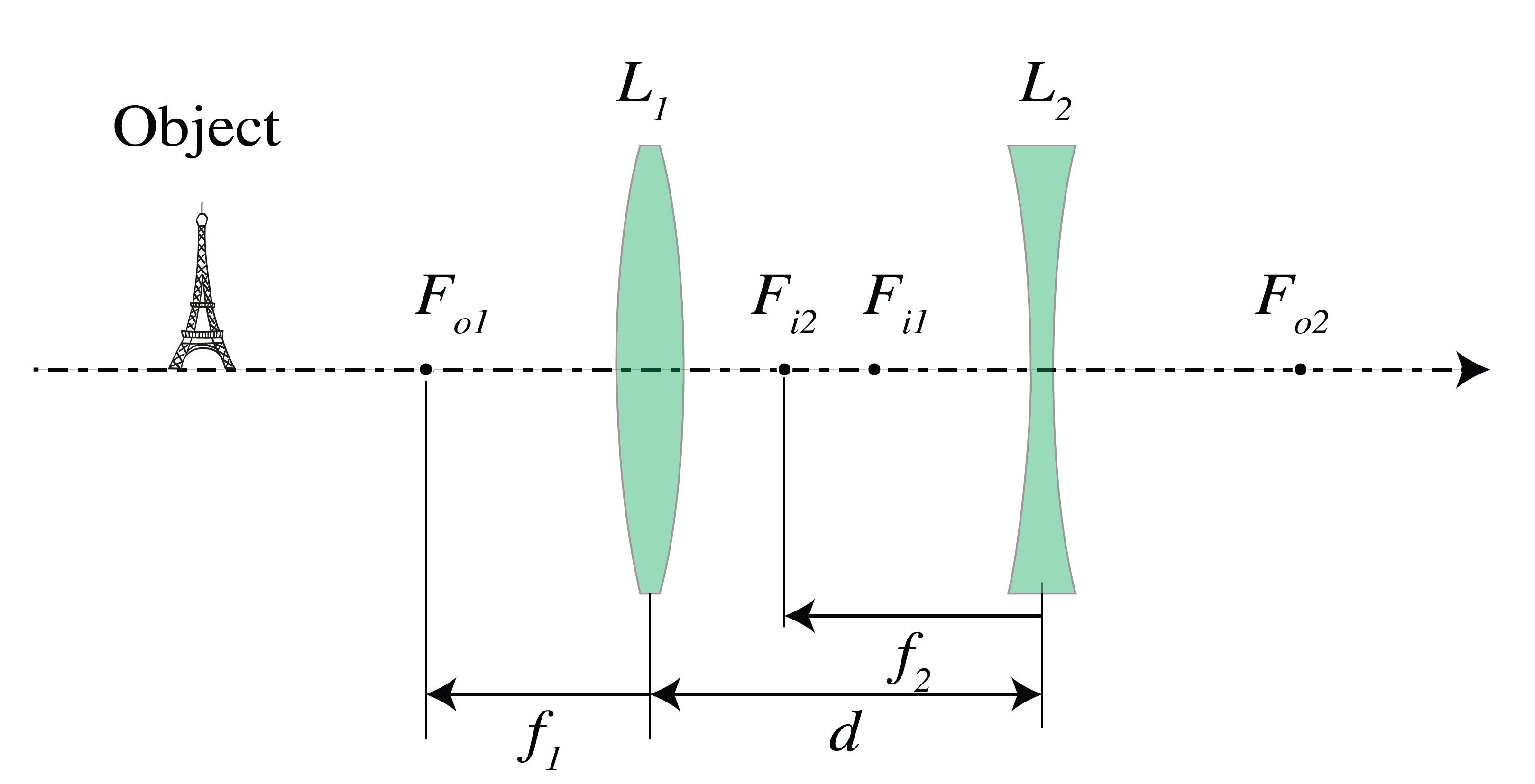
Fig. 44 Figure corresponding to Exercise “A convergent and divergent lens”.

• a) Derive the condition on the distance \(d\) between the lenses such that the final image is real.

• b) Let \(f_1=3 \text{ cm}\) and \(f_2=-2 \text{ cm}\). What should be the distance \(d\) such that the final image is real and the magnification is 2?

6. System matrix for imaging by a spherical surface.

Consider a spherical surface with radius of curvature \(R\) with to the left (right) of the surface a medium with refractive index \(n_1\) (\(n_2\)).

• a) Derive the ray matrix between a plane to the left of the surface and at distance \(d_1\) to the vertex, and a plane to the right of the surface with distance of \(d_2\) to the vertex. (As always the rays are assumed to propagate from the left to the right).

• b) Derive the conditions such that the plane at distance \(d_2\) is the image of the plane at distance \(d_1\). Express the formula in coordinates \(s_o=-d_1\), \(s_i=d_2\) with respect to the vertex as origin and show that the result is identical to formula (182)

• c) Assume that \(n_1=1\), \(n_2=2\) and \(R= 2\) cm. Show by construction using the paraxial version of Snell’s Law that when the object is virtual with \(s_o=-4\) cm, the coordinate of the image point is given by \(s_i= 8\) cm, in agreement with the formula derived in b).

• d) Construct again the image when \(s_o=-4\) cm but now for the case that \(R=-2\) cm and verify that the coordinate \(s_i\) of the image point agrees with the formula derived in b).

7. The purpose of this problem is to derive the Lensmaker’s formula for a thin lens by applying the imaging formula of a spherical surface twice. The image \(P\) of a point \(S\) as shown in Fig. 45 is computed in two steps. First the intermediate image \(P'\) of \(S\) by the spherical surface with vertex \(V_1\) is computed and then this intermediate image is imaged by the spherical surface with vertex \(V_2\).

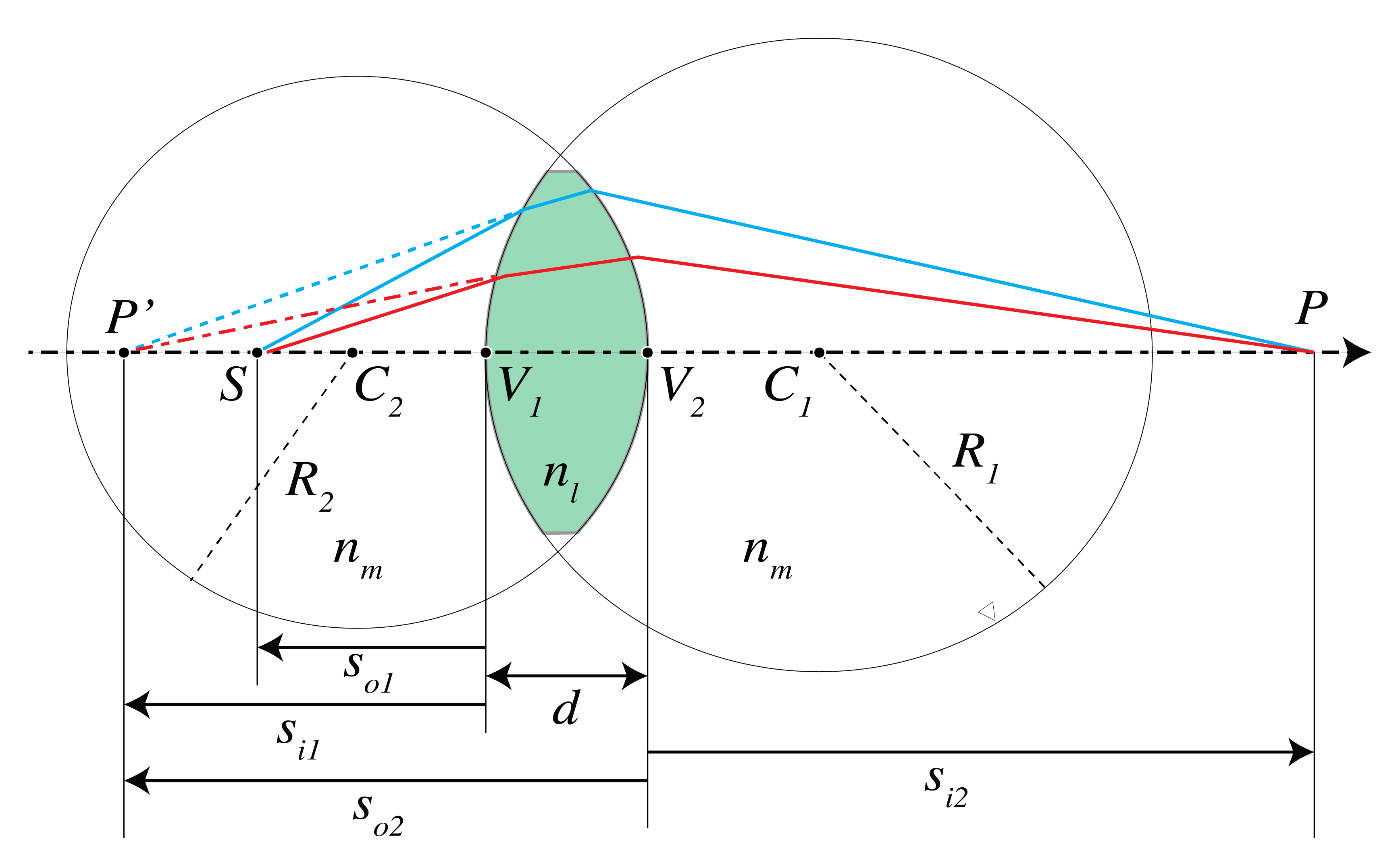
Fig. 45 A spherical lens made of glass of index \(n_l\) in a medium of index \(n_m\). The point \(S\) is imaged in \(P\).

• a) Use (182) to deduce that when \(S\) is imaged by the first spherical surface as if the second spherical surface were absent, the image \(P'\) has \(z\)-coordinate \(s_{i1}\) with respect to the origin in \(V\), of \(S\), satisfies:

\[ -\frac{n_m}{s_{o1}}+\frac{n_l}{s_{i1}} =\frac{n_l-n_m}{R_1},\]

where \(s_{o1}\) is the \(z\)-coordinate of \(S\) with respect to the origin in \(V\).

• b) Show that with respect to the origin at \(V_2\) the \(z\)-coordinate of \(P'\) is

\[ s_{o2}= s_{i1}-d.\]

• c) Show that the \(z\)-coordinate \(s_{i2}\) of P with respect to the origin at \(V_2\) satisfies

\[ -\frac{n_l}{s_{o2}}+\frac{n_m}{s_{i2}}=\frac{n_m-n_l}{R_2}.\]

• d) Add the results of a) and c) to derive

\[ -\frac{n_m}{s_{o1}} + \frac{n_m}{s_{i2}} = (n_l-n_m)\left( \frac{1}{R_1}-\frac{1}{R_2}\right) + \frac{n_l d}{(s_{i1}-d) s_{i1}}.\]

• e) Derive the Lensmaker’s formula for the thin lens (215) by taking the limit \(d\rightarrow 0\) in d).

8. System matrix for focusing.

Consider a ray transfer matrix

(245)\[\begin{split}\begin{align*} \left( \begin{array}{cc}A & B \\C & D \end{array}\right) \end{align*}\end{split}\]

between two planes.

• a) Suppose that any ray that is parallel to the optical axis in the first plane goes through a point on the optical axis in the second plane. This means that the second plane is the image focal plane of the system. What does this imply for the elements of the transfer matrix?

• b) Suppose that the first plane is the object focal plane, so that any ray emitted by the point on the optical axis in the first plane becomes collimated in the second plane. What does this imply for the elements for the transfer matrix?

• c) Consider two thin lenses with distance \(d\) and focal distances \(f_{1i}\) and \(f_{2i}\). Derive the transfer matrix linking the plane immediately before the first lens with the plane immediately behind the second lens. You may assume that the lenses are in air with refractive index \(n=1\).

• d) Use the condition that you found in a) to derive the image focal distance of a system consisting of two thin lenses with image focal distances \(f_{1i}\) and \(f_{2i}\) and distance \(d\). Verify that the result agrees with the distance for the image focal plane (225). Hint: let \(f_i\) be the distance of the image focal point of the two-lens system to the second lens. Write the transfer matrix between the lens immediately before the first lens and the plane through the image focal point.

• e) Add a third thin lens with image focal distance \(f_{3i}\) is in contact to the second lens. Derive the ray matrix of this system.

• f) Let \(f_i\) be the distance from the image focal plane to the third lens. Use the condition derived in a) and the ray matrix derived in e) to derive \(f_i\).

9. Matrix for two thin lenses.

• a) Consider two thin lenses which are surrounded by a medium with refractive index \(n\). Let the left and right lens have power \({\cal P}_1\) and \({\cal P}_2\), respectively and let the distance between their vertices be \(d\). Derive that the matrix between the planes immediately to the left of the first lens and the plane immediately to the right of the second lens is given by

(246)\[\begin{split} \left( \begin{array}{cc}1-\frac{d}{n}{\cal P}_1 & -{\cal P}_1-{\cal P}_2 - \frac{d}{n}{\cal P}_1{\cal P}_2 \\\frac{d}{n} & 1-\frac{d}{n}{\cal P}_2 \end{array}\right). \end{split}\]

• b) Show that the coordinates of the image and object focal points are given by:

(247)\[ f_i = \frac{P_1+P_2 + \frac{d}{n} {\cal P}_1{\cal P}_2}{n \left( 1 - \frac{d}{n}\right){\cal P}_2 } \]

(248)\[ f_o = \frac{P_1+P_2 + \frac{d}{n} {\cal P}_1{\cal P}_2}{n \left( 1 - \frac{d}{n}\right){\cal P}_1 }. \]

• c) Verfify that these formulae are equivalent to (226),(225).

10. Entrance pupil of a system of two lenses. Consider a system of two lenses \(L_1\) and \(L_2\) with distance \(d\). The left lens \(L_1\) has image focal distance \(f_{1i}\) and \(a_1\), \(a_2\) are the radii of the lens apertures of \(L_1\) and \(L_2\).

• a) Let lens \(L_1\) be convergent with \(f_{1i}=2 \text{ cm}\) and let the distance be \(d=1 \text{cm}\). Furthermore, let \(a_1=2 \text{cm}\) and \(a_2= 1\text{cm} \). Determine by construction with a ruler the entrance pupil. Compute also its position and radius using the Lensmakers’ formula and derive the tangent of the angle that the marginal ray makes with the optical axis for an object on the optical axis at 4 cm to the left of \(L_1\).

• b) Same question when \(L_1\) is a divergent lens with \(f_{1i}=-6 \text{ cm}\), \(d=3 \text{ cm}\) and \(a_1=a_2=1 \text{cm}\).

11. Diaphragm in a system of two thin lenses. The purpose of this problem is to determine the entrance and exit apertures of a system consisting of two thin lenses with a diaphragm using three methods: construction, applying the Lensmaker’s formula and the matrix method. The situation is as shown in Fig. 46. The focal distances of the two thin lenses are \(f_1=10\) cm and \(f_2=12\) cm and their distance \(d = 6\) cm. Suppose that the aperture stop is as shown in Fig. 46. It is at a distance of \( 1.5\) cm in front of the lens \(L_1\) and has a diameter \(D_a=5\) cm.

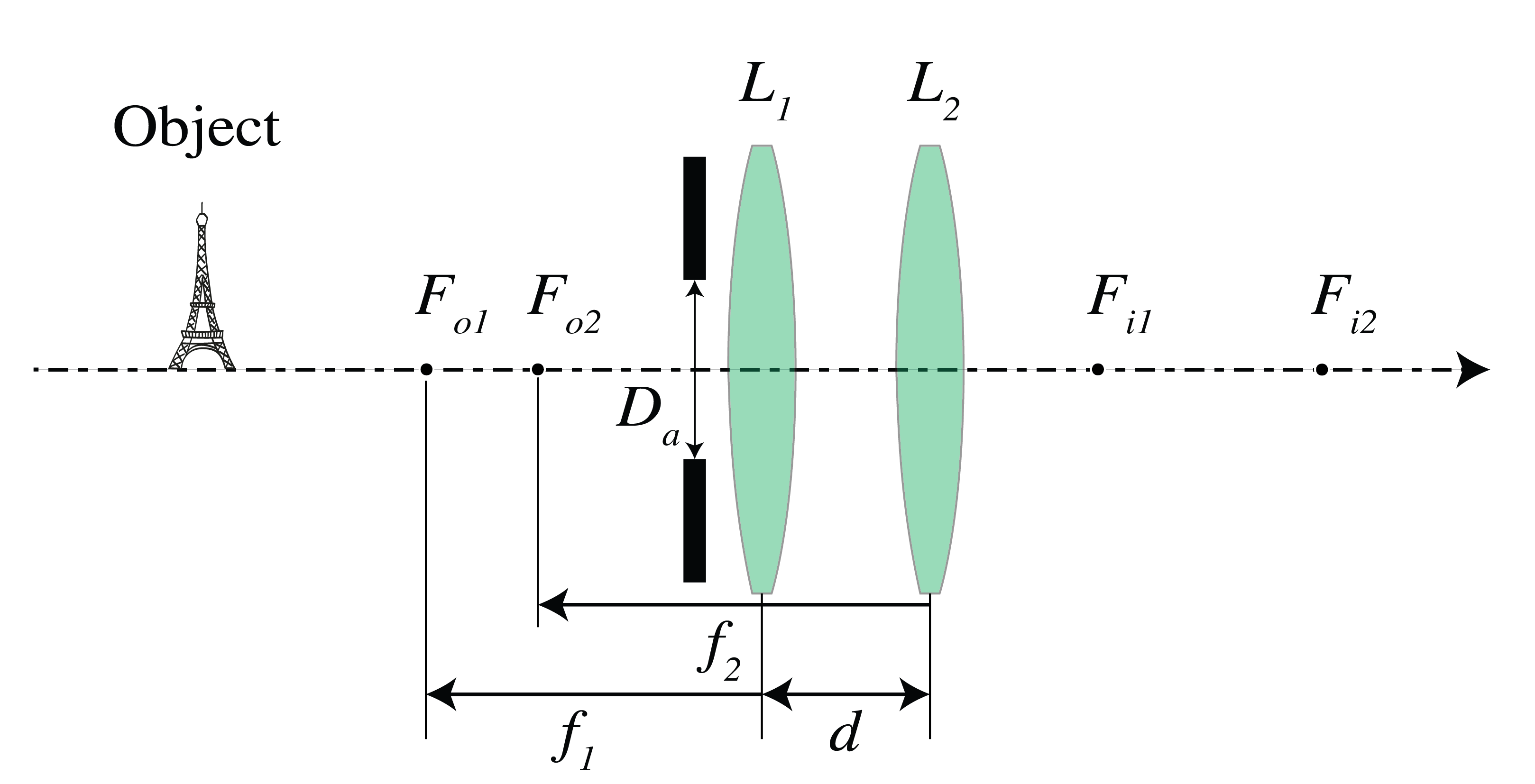
Fig. 46 Two thin lenses

• a) Determine the position of the entrance pupil and its diameter \(D_{e}\) by the mentioned three methods.

• b) Determine the position of the exit pupil and its diameter \(D_{exit}\) by the mentioned three methods.

• c) Compute the \(f\)-number of the system.

12. * Principal planes for a thick lens.

In this problem the transfer matrix for a thick lens is derived. By finding the positions of the principal planes, you will derive that the transfer matrix has the same form as for a thin lens when object, image and focal distances are measured with respect to principle planes.

The transfer matrices which you should use are those for refraction through a spherical interface between two media with refractive indices \(n\), \(n'\) to the left and right of the interface, respectively, and with radius of curvature \(R\):

\[\begin{split} {\cal S} = \left( \begin{array}{cc}1 & -k \\0 & 1 \end{array}\right) \nonumber \end{split}\]

where \(k=(n'-n)/R\), and secondly the matrix \({\cal M}_d\) for propagation through a medium with refractive index \(n\) over a distance \(d\).

Consider a thick lens made of a glass of refractive index \(n\) with thickness \(d\). For paraxial rays, the thickness can be identified with the distance between the vertices \(V_1\) and \(V_2\) of the surfaces of the lens.

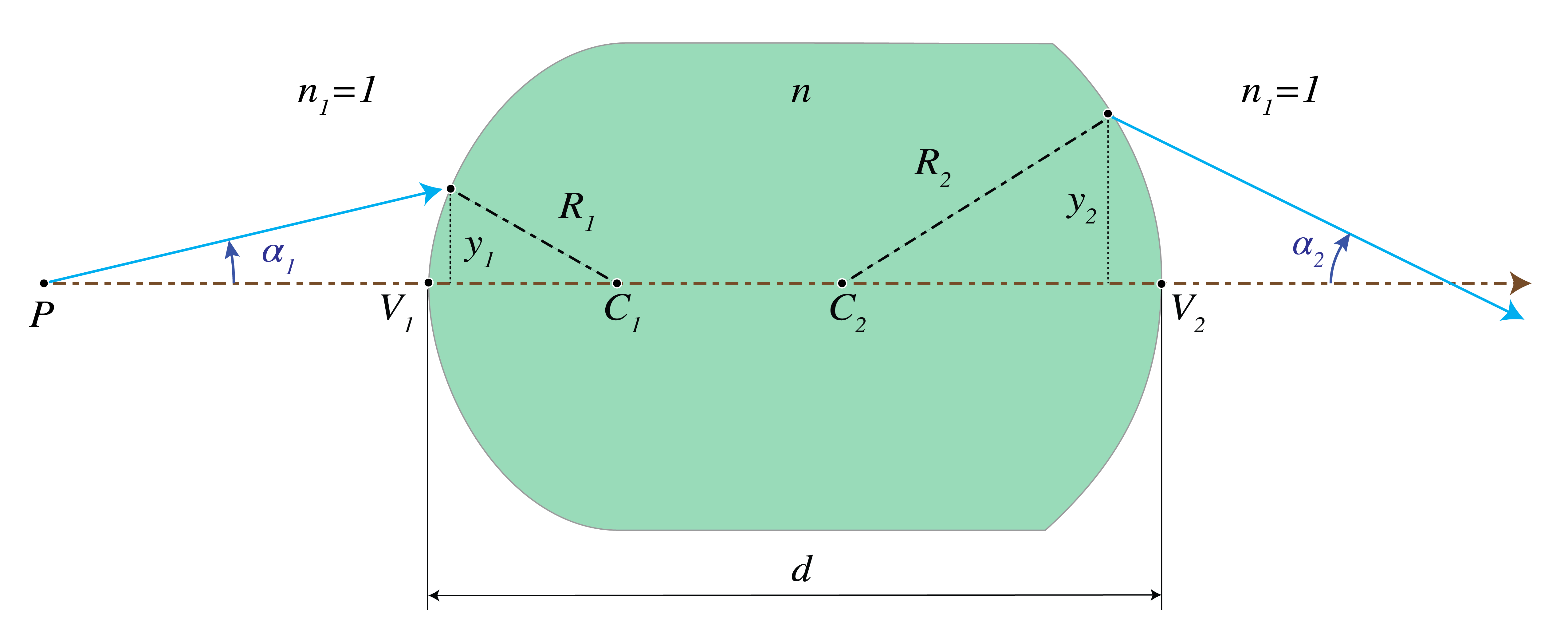
Fig. 47 Thick lens.

• a) Derive that the transfer matrix between the surfaces through the two vertices of the thick lens is given by:

(249)\[\begin{split}\begin{align*} {\cal L}_{V_2V_1} = \left( \begin{array}{cc}1 - k_2 \frac{d}{n} & -k_1 -k_2 + k_1 k_2 \frac{d}{n} \\\frac{d}{n} & 1-k_1 \frac{d}{n} \end{array}\right) \end{align*}\end{split}\]

where \(k_1= (n-1)/R_1\) and \(k_2= (1-n)/R_2\)

• b) Show that for \(d=0\) the transfer matrix is identical to that for a thin lens given by Eq. (206).

In Section 3.5.7 of the Lecture Notes the primary and secondary principle planes were defined. Let the distance between the primary principle plane \({\cal H}_1\) and vertex \(V_1\) be \(T_1\), and let the distance of the second principle plane \({\cal H}_2\) to vertex \(V_2\) be \(T_2\) as shown in Fig. 48). \(T_1>0\) and \(T_2>0\) if the first principle plane is to the left of \(V_1\) and the second principle plane is to the right of \(V_2\), respectively, while \(T_1\) and \(T_2\) are negative otherwise.

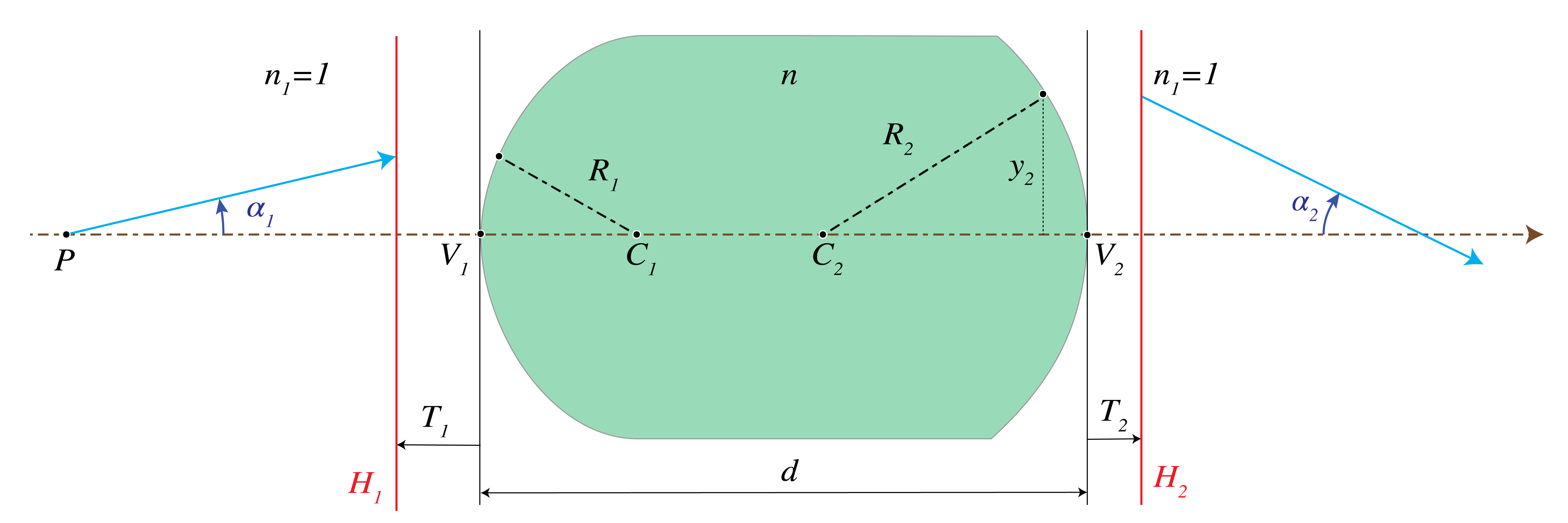
Fig. 48 Thick lens with principle planes.

The transformation of a ray from the primary principle plane \({\cal H}_1\) to the secondary principle plane \({\cal H}_2\) is:

(250)\[\begin{split} \left( \begin{array}{c}\alpha_1 \\y_1 \end{array}\right) = {\cal L}_{{\cal H}_1{\cal H}_2} \left( \begin{array}{c}\alpha_2 \\y_2 \end{array}\right), \end{split}\]

where

\[\begin{align*} {\cal L}_{{\cal H}_2{\cal H}_1} = {\cal M}_{ T_2} {\cal L}_{V_2 V_1} {\cal M}_{T_1}, \end{align*}\]

• c) By using the following abbreviation for the matrix (249):

(251)\[\begin{split}\begin{align*} \left( \begin{array}{cc}1 - k_2 \frac{d}{n} & -k_1 -k_2 + k_1 k_2 \frac{d}{n} \\\frac{d}{n} & 1-k_1 \frac{d}{n} \end{array}\right) = \left( \begin{array}{cc}a_{11} & a_{12} \\a_{21} & a_{22} \end{array}\right), \end{align*}\end{split}\]

derive that:

(252)\[\begin{split}\begin{align*} {\cal L}_{{\cal H}_2{\cal H}_1} = \left( \begin{array}{cc}a_{11} + T_1 a_{12} & \; a_{12} \\T_2 (a_{11} +T_1 a_{12}) + a_{21} + T_1 a_{22} & \; a_{22} + T_2 a_{12} \end{array}\right) \end{align*}\end{split}\]

• d) The principle planes are conjugate (i.e. they are each other images) with unit magnification. Derive from this fact that the locations of the principle planes are given by:

\[\begin{split}\begin{align*} T_2&=\frac{1-a_{22}}{a_{12} }\\ T_1&= \frac{1-a_{11}}{a_{12}} \end{align*}\end{split}\]

With the solutions for \(T_1\) and \(T_2\) the system matrix between the principal planes becomes:

(253)\[\begin{split} {\cal L}_{{\cal H}_2{\cal H}_1} = \left( \begin{array}{cc}1 & a_{12} \\0 & 1 \end{array}\right) \end{split}\]

which has the same shape as the transfer matrix for a thin lens.

• e) Show that the back focal point is at distance \(1/a_{12}\) from the secondary principle plane and that the front focal plane is at distance \(1/a_{12}\) from the primary principle plane.