Waves

12. Waves#

In physics a wave is a disturbance or oscillation that travels through space accompanied by a transfer of energy, and may be propagated with little or no net motion of the medium involved. In this section we will consider mechanical waves, in which the particles in a material are oscillating. Examples are the waves in the sea, the wave in the crowd at a stadium, and sound. Later on we will encounter electromagnetic waves in which electric and magnetic fields are oscillating, and which can travel through vacuum. Examples are light and radio signals. In quantum mechanics, we will also encounter what are sometimes referred to as matter waves, where fundamental objects that we usually think of as particles, such as electrons and protons, can also be considered as waves. Finally, recently gravitational waves were discovered, which are vibrations of spacetime itself.

By observing a particle, we know in which direction it moves at any given time. However, as I just stated, the particles in a mechanical wave have no, or almost no, net motion as the wave passes. The wave does have a well-defined direction though: the direction in which energy is transferred. Some waves spread out uniformly, such as a sound wave emanating from a point source. Others are restricted in their motion by the properties of the material they travel in, such as a wave in a string, or by boundary conditions, such as the end of that string. For waves that move (predominantly) in one direction, we can distinguish two fundamental types, illustrated in Fig. 12.1. The first type is the case that the particles oscillate in the same direction as the wave is moving (Fig. 12.1a), which we call a longitudinal wave; sound is an example. The second case is that the particles oscillate in a direction perpendicular to the wave motion, which we call a transverse wave (Fig. 12.1b), of which the waves in a pond are an example.

../_images/wavetypes.svg

Fig. 12.1 Two basic types of waves. (a) Longitudinal wave, where the oscillatory motion of the particles is in the same direction as that of the wave. (b) Transverse wave, where the oscillatory motion of the particles is perpendicular to that of the wave.#

12.1. Sinusoidal waves#

Probably the simplest kind of wave is a transverse sinusoidal wave in a one-dimensional string. In such a wave each point of the string undergoes a harmonic oscillation. We will call the displacement from equilibrium \(u\), then we can plot \(u\) as a function of position on the string at a given point in time, Fig. 12.2a, which is a snapshot of the wave. Alternatively, we can plot \(u\) as a function of time for a given point (with given position) on the string, Fig. 12.2b. Because the oscillation is harmonic, the displacement as a function of time is a sine function, with an amplitude (maximum displacement) \(A\) and a period (time between maxima) \(T\).

By definition, each point of the string undergoing a sinusoidal wave undergoes a harmonic oscillation, so for each point we can write \(u(t) = A \cos(\omega t + \phi)\) (equation (8.4)), where as before \(\omega = 2\pi/T\) is the (angular) frequency and \(\phi\) the phase. Two neighboring points on the string are slightly out of phase - if the wave is traveling to the right, then your right-hand neighbor will reach maximum slightly later than you, and thus has a slightly larger phase. The difference in phase is directly proportional to the distance between two points, coming to a full \(2\pi\) (which is of course equivalent to zero) after a distance \(\lambda\), the wavelength. The wavelength is thus the distance between two successive points with the same phase, in particular between two maxima. In between these maxima, the phase runs over the full \(2\pi\), so the wave is also a sinusoid in space, with a ‘spatial frequency’ or wavenumber \(k = 2\pi / \lambda\). Combining the dependencies on space and time in a single expression, we can write for the sinusoidal wave:

(12.1)#\[ u(x, t) = A \cos(k x - \omega t). \]

The speed of the wave is the distance the wave travels per unit time. A unit time for a wave is one period, as that is the time it takes the oscillation to return to its original point. The distance traveled in one period is one wavelength, as that is the distance between two maxima. The speed is therefore simply their ratio, which can also be expressed in terms of the wave number and frequency:

(12.2)#\[ v_\mathrm{w} = \frac{\lambda}{T} = \frac{\omega}{k}. \]
../_images/simplesinusoidalwave.svg

Fig. 12.2 A sinusoidal transverse wave in space (a) and time (b). The distance between two successive maxima (or any two successive points with equal phase is the wavelength \(\lambda\) of the wave. The maximum displacement is the amplitude \(A\), and the time it takes a single point to go through a full oscillation is the period \(T\).#

12.2. The wave equation#

As with all phenomena in classical mechanics, the motion of the particles in a wave, for instance the masses on springs in Fig. 12.1, are governed by Newton’s laws of motion and the various force laws. In this section we will use these laws to derive an equation of motion for the wave itself, which applies quite generally to wave phenomena. To do so, consider a series of particles of equal mass \(m\) connected by springs of spring constant \(k\), again as in Fig. 12.1a, and assume that at rest the distance between any two masses is \(h\). Let the position of particle \(i\) be \(x\), and \(u\) the distance that particle is away from its rest position; then \(u = x_\mathrm{rest}-x\) is a function of both position \(x\) and time \(t\). Suppose particle \(i\) has moved to the left, then it will feel a restoring force to the right due to two sources: the compressed spring on its left, and the extended spring on its right. The total force to the right is then given by:

(12.3)#\[\begin{split}\begin{align*} F_i &= F_{i+1 \to i} - F_{i-1 \to i} \\ &= k\left[u(x+h,t) - u(x,t)\right] - k\left[u(x,t) - u(x-h,t)\right] \\ &= k\left[u(x+h,t) - 2u(x,t) + u(x-h,t)\right] \end{align*}\end{split}\]

Equation (12.3) gives the net force on particle \(i\), which by Newton’s second law of motion (equation (2.5)) equals the particle’s mass times its acceleration. The acceleration is the second time derivative of the position \(x\), but since the equilibrium position is a constant, it is also the second time derivative of the distance from the equilibrium position \(u(x,t)\), and we have:

(12.4)#\[ F_\mathrm{net} = m \frac{\partial^2 u(x,t)}{\partial t^2} = k\left[u(x+h,t) - 2u(x,t) + u(x-h,t)\right]. \]

Equation (12.4) holds for particle \(i\), but just as well for particle \(i+1\), or \(i-10\). We can get an equation for \(N\) particles by simply adding their individual equations, which we can do because these equations are linear. We thus find for a string of particles of length \(L=Nh\) and total mass \(M=Nm\):

(12.5)#\[ \frac{\partial^2 u(x,t)}{\partial t^2} = \frac{K L^2}{M} \frac{u(x+h,t) - 2u(x,t) + u(x-h,t)}{h^2}. \]

Here \(K=k/N\) is the effective spring constant of the \(N\) springs in series. Now take a close look at the fraction on the right hand side of equation (12.5): if we take the limit \(h \to 0\), this is the second derivative of \(u(x,t)\) with respect to \(x\). However, taking \(h\) to zero also takes \(L\) to zero - which we can counteract by simultaneously taking \(N\to\infty\), in such a way that their product \(L\) remains the same. What we end up with is a string of infinitely many particles connected by infinitely many springs - so a continuum of particles and springs, for which the equation of motion is given by the wave equation:

(12.6)#\[ \frac{\partial^2 u(x,t)}{\partial t^2} = v_\mathrm{w}^2 \frac{\partial^2 u(x,t)}{\partial x^2}. \]

In equation (12.6), \(v_\mathrm{w} = \sqrt{K L^2/M}\) (sometimes also denoted by \(c\)) is the wave speed.

For a wave in a taut string, the one-dimensional description is accurate, and we can relate our quantities \(K\), \(L\) and \(M\) to more familiar properties of the string: its tension \(T=K L\) with the dimension of a force (this is simply Hooke’s law again) and its mass per unit length \(\mu = M/L\), so we get

(12.7)#\[ v_\mathrm{string} = \sqrt{\frac{T}{\mu}}. \]

In two or three dimensions, the spatial derivative in equation (12.6) becomes a Laplacian operator, and the wave equation is given by:

(12.8)#\[ \frac{\partial^2 u(\bm{x},t)}{\partial t^2} = v_\mathrm{w}^2 \nabla^2 u(\bm{x},t) \]

As can be readily seen by writing equation (12.8) in terms of spherical coordinates, if the wave is radial (i.e., only depends on the distance to the source \(r\), and not on the angle), the quantity \(r u(r)\) obeys the one-dimensional wave equation, so we can write down the equation for \(u(r)\) immediately. An important application are sound waves, which spread uniformly in a uniform medium. To find their speed, we characterize the medium in a similar fashion as we did for the string: we take the mass per unit volume, which is simply the density \(\rho\), and the medium’s bulk modulus, which is a measure for the medium’s resistance to compression (i.e., a kind of three-dimensional analog of the spring constant), defined as:

(12.9)#\[ B = - V \frac{\mathrm{d}p}{\mathrm{d}V} = \rho \frac{\mathrm{d}p}{\mathrm{d}\rho}, \]

where \(p\) is the pressure (force per unit area) and \(V\) the volume. The bulk modulus is also sometimes denoted as \(K\). The dimensions of the bulk modulus are those of a pressure, or force per unit area, and those of the density are mass per unit volume, so their ratio has the dimension of a speed squared, and the speed of sound is given by:

(12.10)#\[ v_\mathrm{sound} = \sqrt{\frac{B}{\rho}} \]

Equation (12.8) describes a wave characterized by a one-dimensional displacement (either longitudinal or transverse) in three dimensions. In general a wave can have components of both, and the displacement itself becomes a vector quantity, \(\bm{u}(\bm{x}, t)\). In that case the three-dimensional wave equation takes on a more complex form:

(12.11)#\[ \rho \frac{\partial^2 \bm{u}(\bm{x},t)}{\partial t^2} = \bm{f} + (B+\frac43 G) \nabla (\nabla \cdot \bm{u}(\bm{x},t)) - G \nabla \times (\nabla \times \bm{u}(\bm{x},t)), \]

where \(\bm{f}\) is the driving force (per unit volume), \(B\) again the bulk modulus, and \(G\) the material’s shear modulus. Equation (12.11) is used for the description of seismic waves in the Earth and the ultrasonic waves with which solid materials are probed for defects.

12.3. Solution of the one-dimensional wave equation#

The one-dimensional wave equation (12.6) has a surprisingly generic solution, due to the fact that it contains second derivatives in both space and time. As you can readily see by inspection, the function \(q(x,t) = x - v_\mathrm{w} t\) is a solution, as is the same function with a plus instead of a minus sign. These functions represent waves traveling to the right (minus) or left (plus) at speed \(v_\mathrm{w}\). However, the shape of the wave does not matter - any function \(F(q) = F(x - v_\mathrm{w} t)\) is a solution of (12.6), as is any function \(G(x + v_\mathrm{w} t)\), and the general solution is the sum of these:

(12.12)#\[ u(x, t) = F(x - v_\mathrm{w} t) + G(x + v_\mathrm{w} t). \]

To find a specific solution, we need to look at the initial conditions of the wave, i.e., the conditions at \(t=0\). Because the wave equation is second order in time, we need to specify both the initial displacement and the displacement’s initial velocity, which can be functions of the position. For the most general case we write:

(12.13)#\[\begin{split}\begin{align*} u(x, 0) &= u_0(x), \\ \dot{u}(x, 0) &= v_0(x). \end{align*}\end{split}\]

The resulting solution of the one-dimensional wave equation is known as d’Alembert’s equation:

(12.14)#\[ u(x, t) = \frac12 \left( u_0(x-v_\mathrm{w} t) + u_0(x+v_\mathrm{w} t) \right) + \frac{1}{2 v_\mathrm{w}} \int_{x-v_\mathrm{w} t}^{x+v_\mathrm{w} t} v(y) \,\mathrm{d}y. \]

12.4. Wave superposition#

The wave equation (12.6) is linear in the function we’re interested in, the displacement \(u(x,t)\). This simple mathematical statement has important consequences, because it means that if we know any set of solutions, we can create more solutions by making linear combinations of them - so if \(u_1(x,t)\) and \(u_2(x,t)\) are solutions, then so are \(a u_1(x,t) + b u_2(x,t)\) for any choice of \(a\) and \(b\). In physics, this useful property of linear differential equations is known as the principle of superposition. Thanks to this principle, we can study how different waves interact with each other without having to do (much) extra math.

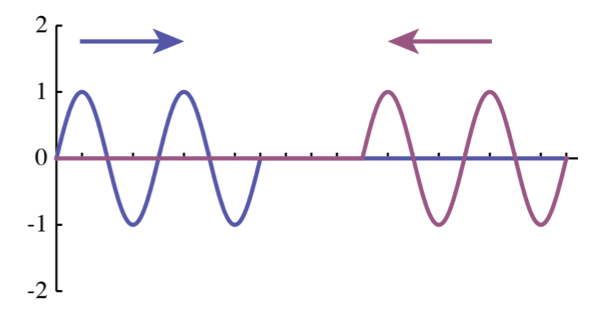
To illustrate, let us consider two one-dimensional waves traveling in opposite directions, Fig. 12.3. As long as the waves do not overlap, the oscillation of any given particle is due to only one wave, and there is no interaction. However, as soon as the waves start overlapping, the oscillations add up, which leads to interference. At some points, the two oscillations will be in phase, resulting in a much larger oscillation amplitude, which we call constructive interference (Fig. 12.3b). At other points, the two oscillations will be out of phase, resulting in a much smaller, or even vanishing oscillation amplitude, which we call destructive interference (Fig. 12.3c). However, the waves themselves remain unaffected, and transmit right through each other, continuing their path as if nothing had happened (Fig. 12.3d).

../_images/interference.svg

Fig. 12.3 Two interacting wave packets. The sequence of images shows four snapshots. The blue wave is traveling to the right, the red wave to the left (a). When the waves overlap, the total displacement of the particle is given by the sum of the displacements due to both waves, shown in green. This can lead to both constructive interference (b), when the two waves are in phase, and destructive interference (c), when their phases are opposite. The waves themselves are not affected by the interaction and afterwards travel on as if nothing has happened (d).#

Waves reaching the end of a string, or edge of a pond, or any type of boundary, will not simply disappear. Remember, waves carry energy, and that energy is conserved, so it has to go somewhere once the wave reaches the boundary. If there’s nothing at the boundary, the waves are reflected back into the material. This happens in two cases: a (perfectly) fixed boundary, and a (perfectly) free boundary; in other cases, some of the energy may be transmitted to material on the other side of the boundary (starting a new wave there), whereas the remainder is reflected back into the original material with less energy, resulting in a smaller wave amplitude. A reflected wave travels in the opposite direction to the original wave, so it can interfere with itself. In fact, this interference is a crucial point for being able to meet the boundary conditions. A fixed boundary cannot move, so there must be destructive interference keeping the amplitude there zero at all times - so it follows that a wave reflecting on a fixed boundary undergoes a \(\pi\) phase shift. Free boundaries on the other hand are perfectly free to move, so there is nothing holding it back from reaching the maximal displacement that can be achieved by constructive interference, and the wave reflects without a phase shift.

If you put boundaries on both ends of a string, the wave keeps reflecting back and forth, continuously interfering with itself. To find the resulting shape of the string, we’re going to use the principle of superposition for a simple sinusoidal wave. Let \(u_1(x,t) = A \cos(kx-\omega t)\) be the part of the wave traveling to the right, and \(u_2(x,t) = - A \cos(kx + \omega t)\) be the part traveling to the left. Note the differences: the waves have opposite signs for their speeds, and opposite signs for their displacements, the latter because of the \(\pi\) phase shift (we could also write \(u_2(x,t) = A \cos(kx + \omega t + \pi)\)). The shape of the string is now simply the sum of these two waves:

(12.15)#\[\begin{split}\begin{align*} u(x,t) &= u_1(x,t) + u_2(x,t) = A \left[ \cos(kx-\omega t) - \cos(kx+\omega t) \right] \\ &= 2 A \sin(kx) \sin(\omega t). \end{align*}\end{split}\]

Equation (12.15) tells us that for a self-interfering wave, the wave no longer moves - instead, each point simply oscillates with frequency \(\omega\) at a position-dependent amplitude \(2 A \sin(kx)\). We call such a wave a standing wave. Standing waves are very common - you’ll get one every time you’ll touch the string of a guitar or violin. Naturally, they are not restricted to one-dimensional systems - the skin of a drum, constrained at the drum’s edge, is put in a standing wave every time someone hits it.

Equation (12.15) describes the shape of a standing wave on a string clamped at both ends. If the string has length \(L\), then by the nature of the boundary conditions, we must have \(u(0,t) = u(L,t) = 0\) for all \(t\). The first condition follows for free (which is of course just due to a good choice of coordinates), but the second puts a constraint on our wave. The displacement can only be zero at all times if the amplitude is identically zero, so we demand that \(\sin(kL) = 0\), or \(L = m \pi /k = m \lambda / 2\), where \(m\) is any positive integer. There are thus infinitely many allowed standing waves, but they are characterized by a discrete number. The allowed waves are known as modes, and the associated number \(m\) is the mode number. The simplest wave, with the lowest possible value, \(m=1\), is known as the fundamental mode. In the fundamental mode, the oscillation of the string has nonzero amplitude everywhere but at the fixed ends; for higher modes, there are also points in between that have zero amplitude, which are known as nodes; points where the amplitude is maximum are sometimes referred to as antinodes.

A discrete spectrum of allowed solutions, characterized by integer numbers, does not only appear in standing mechanical waves, but is also a fundamental aspect of quantum mechanics.

../_images/standingwaves.svg

Fig. 12.4 Snapshots of the wave patterns for the first three modes of a standing wave in (a) a string with two clamped ends, (b) a string with one clamped end, or a tube with one closed and one open end, and (c) a tube with two open ends. In each case, the plot shows the amplitude of the standing wave, as a fraction of the amplitude of the traveling wave. At nodes, the amplitude of the standing wave vanishes: destructive interference causes these points to always stand still. At antinodes, the amplitude of the standing wave is maximal, and equals that of the traveling wave. Note that (a) and (b) will occur for transversal waves, whereas (b) and (c) will occur for sound waves. For cases (a) and (c) allowed wavelengths are \(\lambda = 2L / n\), whereas for case (b), allowed wavelengths are \(\lambda = 4L / (2n-1)\).#

../_images/c10q3_boundaries.svg
../_images/c10q4_interference.png

12.5. Amplitude modulation#

So far, we’ve mostly considered simple sinusoidal waves with fixed amplitudes. However, the general solution to the wave equation allows for many more interesting wave shapes. An important, and often encountered one is where the wave itself is used as the medium, by changing the amplitude over time:

(12.16)#\[ u(x,t) = A(x,t) \cos(k x - \omega t). \]

The wave now consists of two waves: the carrier wave, which travels with the phase velocity \(v_\mathrm{w} = \omega/k\), and the envelope, which travels with the group velocity \(v_\mathrm{g}\). An illustration of a modulated wave is shown in Fig. 12.5. In the common case that the group velocity is independent of the wavelength of the carrier wave, we can rewrite (12.16) to reflect the fact that the amplitude is now also a wave, with speed \(v_\mathrm{g}\):

(12.17)#\[ u(x,t) = A(x - v_\mathrm{g} t) \cos(k x - \omega t). \]
../_images/modulatedwave.svg

Fig. 12.5 Amplitude-modulated wave. The amplitude of the carrier wave (blue, traveling at phase velocity \(v_\mathrm{w} = \omega/k\)) is changed over time, resulting in an envelope (red) which travels at the lower group velocity \(v_\mathrm{g}\).#

12.6. Sound waves#

So far, we mostly considered transversal waves, which include waves in strings and waves on the surface of a pond, and are easily visualized. Longitudinal waves, on the other hand, are somewhat harder to draw, but easily heard - as sound is the prime example of a longitudinal wave. Other examples include (some forms of) seismic waves and ultrasound. Many people simply lump all of these together, and use the terms ‘sound waves’ and ‘longitudinal waves’ as synonyms.

We already touched upon the speed of sound waves in Section 12.2 (equation (12.10)). This speed indicates how fast the wavefronts of a sound wave travel; a wavefront is defined as the surface (in three dimensions) where all points have the same phase[1]. To visualize a sound wave we draw a succession of wavefronts one wavelength (or one period) apart. Simple examples include a point source (generating spherical wavefronts) and a planar wave, in which all wave fronts are parallel planes (see Fig. 12.6). The (local) direction of propagation of the wave is the direction perpendicular to the wavefronts, sometimes depicted by a ray.

../_images/wavefronts.svg

Fig. 12.6 Snapshots of the wavefronts (points with equal phase) of a longitudinal wave for (a) a point source (with spherical wavefronts) and (b) a planar wave (where all wavefronts are parallel planes). Successive wavefronts are separated by one wavelength.#

Like transversal waves, longitudinal waves exhibit interference, both with other waves they encounter, and by their own reflections. There can therefore be traveling and standing sound waves. Unlike transversal waves on strings however, longitudinal sound waves are typically created in tubes that are open on either one or both ends. A closed end represents a fixed point, just like the fixed end of a string does, resulting in a stringent boundary condition: the interference between the incoming and outgoing wave must be such that the net displacement at the closed end is zero. An open end corresponds to a transversal wave in a string that is not clamped. As the string in that case is free to move, its maximum displacement will equal the amplitude of the wave. In other words, while a closed end corresponds to a node, the open end corresponds to an antinode. For a string (or pipe) with one clamped / closed and one open end, the wavelength of the lowest-order mode (known as the fundamental mode or first harmonic) therefore equals four times the length \(L\) of the string / pipe. The next mode (second harmonic) will have a wavelength of \(4L/3\), and so on (see Fig. 12.4b), resulting in \(\lambda = 4L/(2n-1)\) for the \(n\)th mode. For a tube with two open ends, the fundamental mode is the inverse of that of a string with two clamped ends - so two antinodes at the ends, and a node in the middle (Fig. 12.4c). Like for a clamped string, the allowed wavelengths are therefore \(\lambda = 2L/n\).

12.7. The Doppler effect#

The Doppler effect is a physical phenomenon that most people have experienced many times: when a moving source of sound (say an ambulance, or more exactly its siren) is approaching you, its pitch sounds noticeably higher then after it passed you by and is moving away. The effect is due to the fact that the observed wavelength (and therefore frequency / pitch) of sound corresponds to the distance between two points of equal phase (i.e., two sequential wavefronts). Ultimately, the Doppler effect thus originates in a change in reference frame (the same frames we encountered in Section 4.3): what you hear is indeed different from what the ambulance’s driver hears. The latter is easy: the driver isn’t moving with respect to the siren, so (s)he simply hears it at whatever frequency it is emitting. For the stationary observer however, the ambulance moves between emitting the first and second wave crest, and so their distance (and hence the observed wavelength / frequency) changes, see Fig. 12.8.

../_images/doppler.svg

Fig. 12.8 Doppler effect. The source emits waves with a fixed time interval \(\Delta t\) between successive wavefronts. (a) For observers that are stationary with respect to the source, the distance between wavefronts (in red) is fixed, so they measure the same wavelength as the one emitted by the source. (b) If the source is moving with respect to the observers (here to the right), the observers measure a different distance between arriving wavefronts - compressed (so shorter wavelength / higher frequency) if the source is approaching (green dot), expanded if the source is receding (purple dot).#

Calculating the shift in wavelength is straightforward. Let us call the speed of sound \(v\) and the speed of the source \(u\). The time interval between two wavefronts, as emitted by the source, is \(\Delta t\). In this time interval, the first wavefronts travels a distance \(\Delta s = v \Delta t\), while the source travels a distance \(\Delta x = u \Delta t\). For the observer to which the source is approaching, the actual distance between two emitted wavefronts is thus \(\Delta x' = \Delta s - \Delta x = (v - u) \Delta t\). The actual distance between the wavefronts is the observed wavelength, \(\lambda_\mathrm{obs}\), while the emitted wavelength is \(\lambda = \Delta s = v \Delta t\), so the two are related through

(12.18)#\[ \lambda_\mathrm{obs} = \frac{v-u}{v} \lambda. \]

For a source that is moving away, we simply flip the sign of \(u\); naturally for a stationary source we have \(\lambda_\mathrm{obs} = \lambda\). Note that we could also consider a stationary source and a moving observer: the effect would be exactly the same, where in equation (12.18) we define motion towards the source to be the positive direction.

The Doppler effect is usually expressed in terms of frequency instead of wavelength, but that is a trivial step from equation (12.18), as \(f_\mathrm{obs} = v / \lambda_\mathrm{obs}\) and \(f = v / \lambda\), which gives:

(12.19)#\[ f_\mathrm{obs} = \frac{v}{v-u} f. \]

Although we discussed the Doppler effect here in the context of sound waves, it occurs for any kind of waves - most notably also light.

Note that equation (12.18) predicts that the wavelength is zero if the speed of the source equals the speed of the emitted waves. This case is illustrated in Fig. 12.10a, which shows that the wavefronts pile up. For a source moving faster than the wave speed (Fig. 12.10b), the waves follow the source, creating a conical shock wave, with opening angle given by

(12.20)#\[ \sin\theta = \frac{vT}{uT} = \frac{v}{u}. \]

Both the bow wave of a boat and the sonic boom of a supersonic jet are examples of shock waves.

../_images/shockwaves.svg

Fig. 12.10 Shock waves. Like in Fig. 12.8, the source emits wavefronts with a fixed time interval \(\Delta t\). (a) If the source is moving at the same speed as the emitted wave, the wavefronts all collide, creating a shock wave. (b) For a source moving faster than the speed of the waves, the waves all travel behind the source, creating a conical (shock) wave front (as you may have heard after seeing a jet fighter pass overhead). The blue dot indicates the current position of the source, the green dot that one period ago, the red dot two periods ago.#

12.8. Problems#