Rotational motion, torque and angular momentum

5. Rotational motion, torque and angular momentum#

5.1. Rotation basics#

So far, we’ve been looking at motion that is easily described in Cartesian coordinates, often moving along straight lines. Such kind of motion happens a lot, but there is a second common class as well: rotational motion. It won’t come as a surprise that to describe rotational motion, polar coordinates (or their 3D counterparts the cylindrical and spherical coordinates) are much handier than Cartesian ones[1]. For example, if we consider the case of a disk rotating with a uniform velocity around its center, the easiest way to do so is to specify over how many degrees (or radians) a point on the boundary advances per second. Compare this to linear motion - that is specified by how many meters you advance in the linear direction per second, which is the speed (with dimension \(L/T\)). The change of the angle per second gives you the angular speed \(\omega\), where a counterclockwise rotation is taken to be in the positive direction. The angular speed has dimension \(1/T\), so it is a frequency. It is measured in degrees per second or radians per second. If the angle at a point in time is denoted by \(\theta(t)\), then obviously \(\omega = \dot{\theta}\), just like \(v = \dot{x}\) in linear motion.

In three dimensions, \(\bm{\omega}\) becomes a vector, where the magnitude is still the rotational speed, and the direction gives you the direction of the rotation, by means of a right-hand rule: rotation is in the plane perpendicular to \(\bm{\omega}\), and in the direction the fingers of your right hand point if your thumb points along \(\bm{\omega}\) (this gives \(\bm{\omega}\) in the positive \(\bm{\hat{z}}\) direction for rotational motion in the \(xy\) plane).

Going back to 2D for the moment, let’s call the angular position \(\theta(t)\), then

(5.1)#\[ \omega = \frac{\mathrm{d}\theta}{\mathrm{d}t} = \dot \theta. \]

If we want to know the position \(\bm{r}\) in Cartesian coordinates, we can simply use the normal conversion from polar to Cartesian coordinates, and write

(5.2)#\[ \bm{r}(t) = r \cos(\omega t) \bm{\hat{x}} + r \sin(\omega t) \bm{\hat{y}} = r \bm{\hat{r}}, \]

where \(r\) is the distance to the origin. Note that \(\bm{r}\) points in the direction of the polar unit vector \(\bm{\hat{r}}\). Equation (5.2) gives us an interpretation of \(\omega\) as a frequency: if we consider an object undergoing uniform rotation (i.e., constant radius and constant velocity), in its \(x\) and \(y\)-directions it oscillates with frequency \(\omega\).

As long as our motion remains purely rotational, the radial distance \(r\) does not change, and we can find the linear velocity by taking the time derivative of (5.2):

(5.3)#\[ \bm{v}(t) = \dot{\bm{r}}(t) = - \omega r \sin(\omega t) \bm{\hat{x}} + \omega r \cos(\omega t) \bm{\hat{y}} = \omega r \bm{\hat{\theta}}, \]

so in particular we have \(v=\omega r\). Note that both \(v\) and \(\omega\) denote instantaneous speeds, and equation (5.2) only holds when \(\omega\) is constant. However, the relation \(v=\omega r\) always holds. To see that this is true, express \(\theta\) in radians, \(\theta=s/r\), where \(s\) is the distance traveled along the rotation direction. Then

(5.4)#\[ \omega = \frac{\mathrm{d}\theta}{\mathrm{d}t} = \frac{1}{r} \frac{\mathrm{d}s}{\mathrm{d}t} = \frac{v}{r}. \]

In three dimensions, we find

(5.5)#\[ \bm{v} = \bm{\omega} \times \bm{r}, \]

where \(\bm{r}\) points from the rotation axis to the rotating point.

Unlike in linear motion, in rotational motion there is always acceleration, even if the rotational velocity \(\omega\) is constant. This acceleration originates in the fact that the direction of the (linear) velocity always changes as points revolve around the center, even if its magnitude, the net linear speed, is constant. In that special case, taking another derivative gives us the linear acceleration, which points towards the center of rotation:

(5.6)#\[ \bm{a}(t) = \ddot{\bm{r}}(t) = - \omega^2 r \cos(\omega t) \bm{\hat{x}} + \omega^2 r \sin(\omega t) \bm{\hat{y}} = -\omega^2 r \bm{\hat{r}}. \]

In Section 5.2 below we will use equation (5.6) in combination with Newton’s second law of motion to calculate the net centripetal force required to maintain rotation at a constant rate.

Of course the angular velocity \(\omega\) need not be constant at all. If it is not, we can define an angular acceleration by taking its time derivative:

(5.7)#\[ \alpha = \frac{\mathrm{d}\omega}{\mathrm{d}t} = \ddot{\theta}, \]

or in three dimensions, where \(\bm{\omega}\) is a vector:

(5.8)#\[ \bm{\alpha} = \frac{\mathrm{d}\bm{\omega}}{\mathrm{d}t}. \]

Note that when \(\bm{\alpha}\) is parallel to \(\bm{\omega}\), it simply represents a change in the rotation rate (i.e., a speeding up/slowing down of the rotation), but when it is not, it also represents a change of the plane of rotation.

In both two and three dimensions, a change in rotation rate causes the linear acceleration to have a component in the tangential direction in addition to the radial acceleration (5.6). The tangential component of the acceleration is given by the derivative of the linear velocity:

(5.9)#\[ \bm{a}_\mathrm{t} = \frac{\mathrm{d}\bm{v}}{\mathrm{d}t} = r \frac{\mathrm{d}\bm{\omega}}{\mathrm{d}t} = r \bm{\alpha}. \]

In two dimensions, \(\bm{a}_\mathrm{t}\) points along the \(\pm\bm{\hat{\theta}}\) direction.

Naturally, there are even more complicated possibilities - the radius of the rotational motion can change as well. We’ll look at that case in more detail in Section 6, but first we consider ‘pure’ rotations, where the distance to the rotation axis is fixed.

5.2. Centripetal force#

When you’re rotating at constant angular velocity, the magnitude of your velocity is always the same, but its direction constantly changes - so you’re constantly undergoing an acceleration, as indicated in equation (5.6). Therefore there must be a net force acting on you. We can calculate that net force using Newton’s second law of motion. It is known as the centripetal force and given by:

(5.10)#\[ \bm{F}_\mathrm{cp} = m \bm{a} = - \frac{m v^2}{r} \bm{\hat{r}} = - m \omega^2 r \bm{\hat{r}}. \]

‘Centripetal’ means ‘center-seeking’ (from Latin ‘centrum’ = center and ‘petere’ = to seek). It is important to remember that this is a net resulting force, not a ‘new’ force like that exerted by gravity or a compressed spring. Equation (5.10) is after all just a special case of Newton’s second law of motion.

5.3. Torque#

Anyone who has ever used a lever - that is everyone, presumably - knows how useful they are at augmenting force: you push with a small force at the long end, to produce a large force at the short end, and make the crank turn, stone lift or bottle cap pop off. If the force is at straight angles with the lever arm (the line connecting the point at which you exert the force to the pivot around which your lever rotates), the effect is largest. In that case we define the torque (or moment of force) \(\tau\) as the product of the force and the lever arm length. As only the perpendicular component of the force counts (you’ll simply push or pull on your lever with a parallel component, not make it turn), in a vector setting you need to project on that perpendicular component, so if \(\bm{r}\) (from the pivot to the point at which the force acts) makes an angle \(\theta\) with the force vector \(\bm{F}\), the magnitude of the torque becomes \(\tau = r F \sin\theta\). That’s exactly the magnitude of the cross product of \(\bm{r}\) and \(\bm{F}\), which also has directional information - useful as a torque can be clockwise or counterclockwise. In general we’ll therefore define the torque by:

(5.11)#\[ \bm{\tau} = \bm{r} \times \bm{F}, \]

which makes a counterclockwise torque positive, in correspondence with the definition of the rotation vector \(\bm{\omega}\).

5.4. Moment of inertia#

Suppose we have a mass \(m\) at the end of a massless stick of length \(r\), rotating around the other end of the stick. If we want to increase the rotation rate, we need to apply a tangential acceleration \(\bm{a}_\mathrm{t} = r \bm{\alpha}\), for which by Newton’s second law of motion we need a force \(\bm{F} = m \bm{a}_\mathrm{t} = m r \bm{\alpha}\). This force in turn generates a torque of magnitude \(\tau = r \cdot F = m r^2 \alpha\). The last equality is reminiscent of Newton’s second law of motion, but with force replaced by torque, acceleration by angular acceleration, and mass by the quantity \(m r^2\). In analog with mass representing the inertia of a body undergoing linear acceleration, we’ll identify this quantity as the inertia of a body undergoing rotational acceleration, which we’ll call the moment of inertia and denote by \(I\):

(5.12)#\[ \bm{\tau} = I \bm{\alpha}. \]

Equation (5.12) is the rotational analog of Newton’s second law of motion. By extending our previous example, we can find the moment of inertia of an arbitrary collection of particles of masses \(m_\alpha\) and distances to the rotation axis \(r_\alpha\) (where \(\alpha\) runs over all particles), and write:

(5.13)#\[ I = \sum_\alpha m_\alpha r_\alpha^2, \]

which like the center of mass in Section 4.1 easily generalizes to continuous objects as[2]

(5.14)#\[ I = \int_V (\bm{r}\cdot\bm{r}) \rho \mathrm{d}V = \int_V \rho r^2 \mathrm{d}V. \]

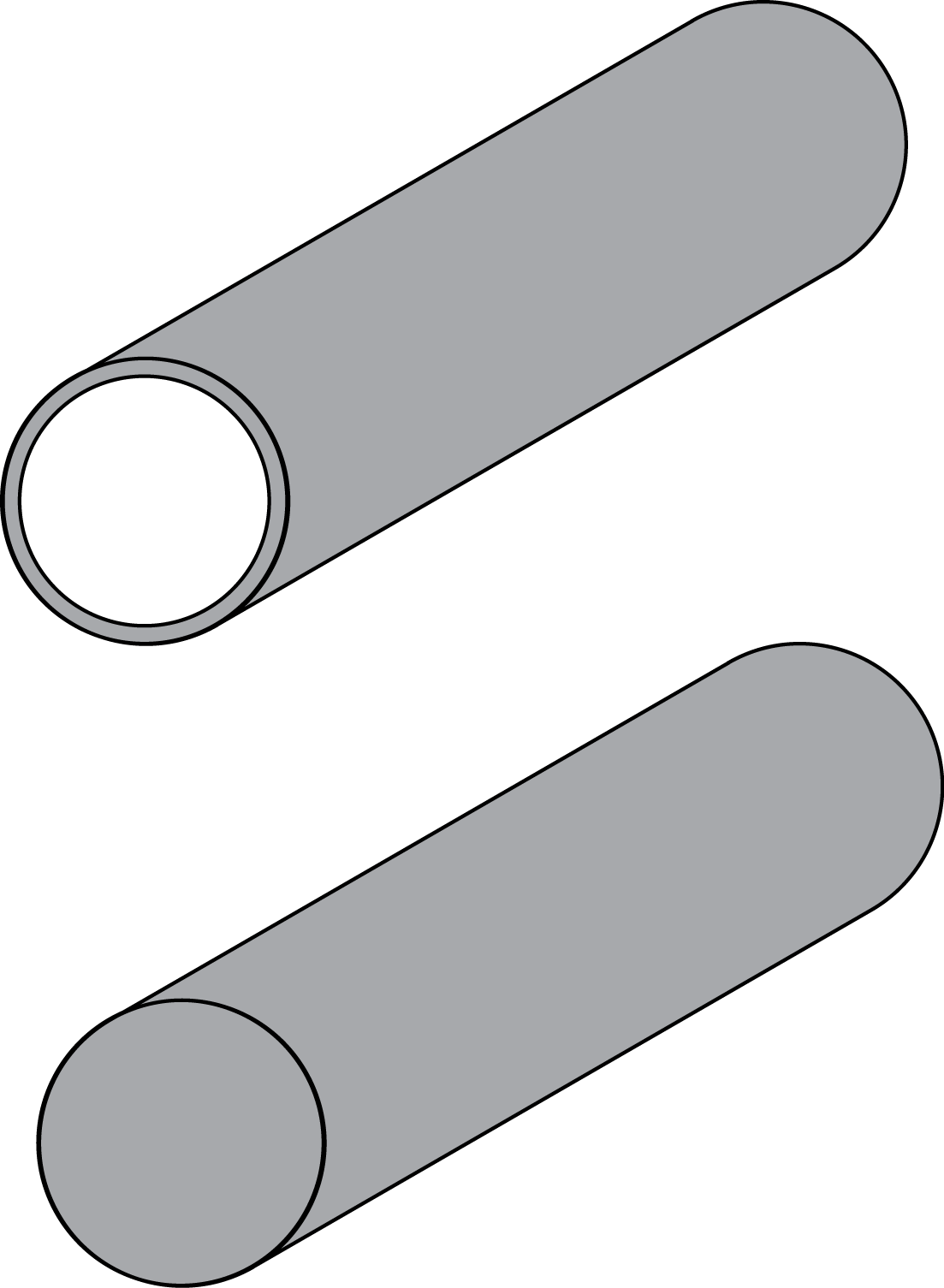
Note that it matters where we choose the rotation axis. For example, the moment of inertia of a rod of length \(L\) and mass \(m\) around an axis through its center perpendicular to the rod is \(\frac{1}{12}mL^2\), whereas the moment of inertia around an axis perpendicular to the rod but located at one of its ends is \(\frac{1}{3}m L^2\). Also, moments of inertia are different for hollow and solid objects - a hollow sphere of mass \(m\) and radius \(R\) has \(\frac23 m R^2\) whereas a solid sphere has \(\frac25 m R^2\), and for hollow and solid cylinders (or hoops and disks) around the long axis through the center we find \(m r^2\) and \(\frac14 m r^2\) respectively. These and some other examples are listed in Table 5.1. Below we’ll relate the moment of inertia to the kinetic energy of a moving-and-rolling object, but first we present two handy theorems that will help in calculating them.

Table 5.1 Moments of inertia for some common objects, all with total mass \(M\) and length \(L\) / radius \(R\).#

Object

Rotation axis

Moment of inertia

Stick

Center, perpendicular to stick

\(\frac{1}{12} M L^2\)

Stick

End, perpendicular to stick

\(\frac{1}{3} M L^2\)

Cylinder, hollow

Center, parallel to axis

\(M R^2\)

Cylinder, solid

Center, parallel to axis

\(\frac12 M R^2\)

Sphere, hollow

Any axis through center

\(\frac23 M R^2\)

Sphere, solid

Any axis through center

\(\frac25 M R^2\)

Planar object, size \(a \times b\)

Axis through center, in plane,

\(\frac{1}{12} M b^2\)

parallel to side with length \(a\)

Planar object, size \(a \times b\)

Axis through center,

\(\frac{1}{12} M (a^2 + b^2)\)

perpendicular to plane

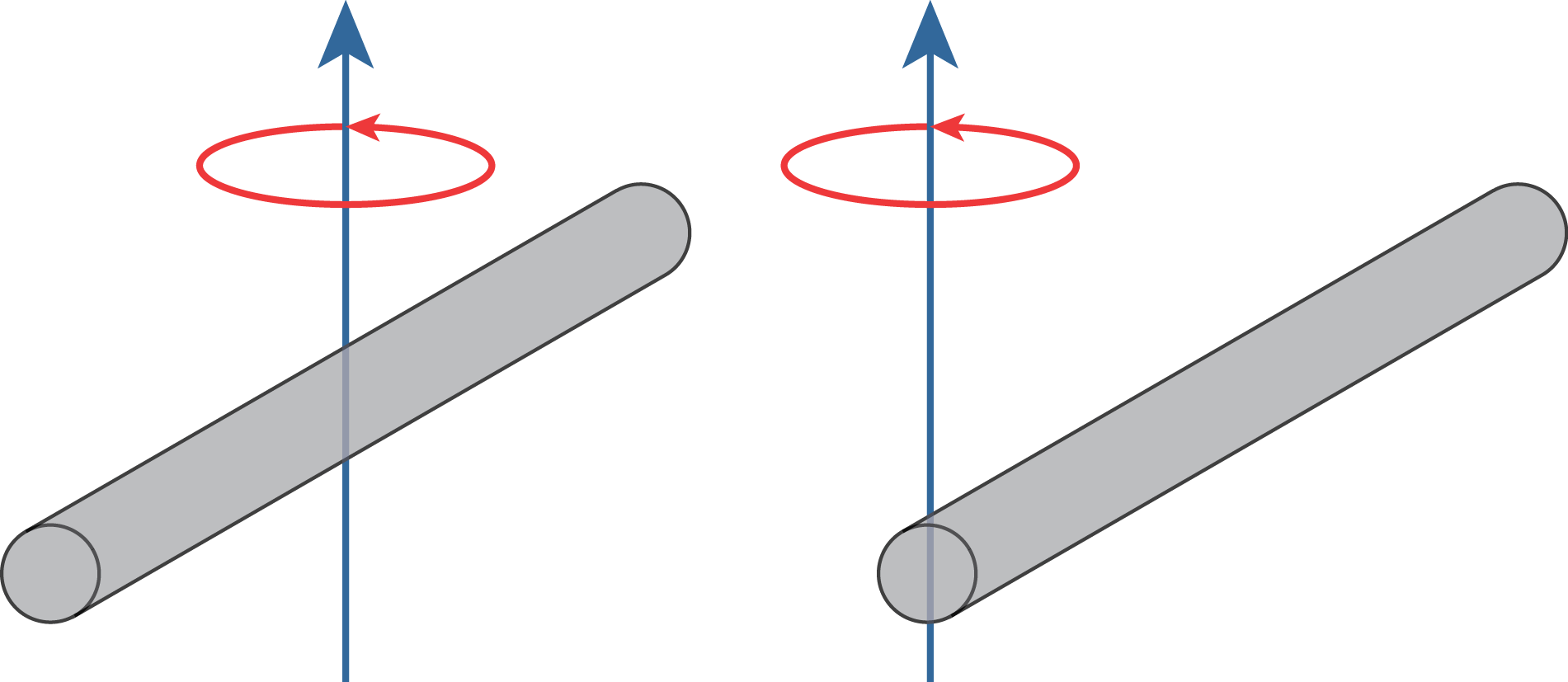
../_images/c6q3_momentofinertia.png
../_images/c6q4_momentofinertia.png

Theorem 5.1 (Parallel axis theorem)

If the moment of inertia of a rigid body about an axis through its center of mass is given by \(I_\mathrm{cm}\), then the moment of inertia around an axis parallel to the original axis and separated from it by a distance \(d\) is given by

(5.15)#\[ I = I_\mathrm{cm} + m d^2, \]

where \(m\) is the object’s mass.

Proof. Choose coordinates such that the center of mass is at the origin, and the original axis coincides with the \(\bm{\hat{z}}\) axis. Denote the position of the point in the \(xy\) plane through which the new axis passes by \(\mathbf{d}\), and the distance from that point for any other point in space by \(\mathbf{r}_d\), such that \(\mathbf{r} = \mathbf{d} + \mathbf{r}_d\). Now calculate the moment of inertia about the new axis through \(\mathbf{d}\):

(5.16)#\[\begin{split}\begin{align*} I &= \int_V (\bm{r}_d \cdot \bm{r}_d) \rho \,\mathrm{d}V \\ &= \int_V (\mathbf{r} \cdot \mathbf{r} + \mathbf{d} \cdot \mathbf{d} - 2 \mathbf{d} \cdot \mathbf{r}) \rho \,\mathrm{d}V \\ &= I_\mathrm{cm} + m d^2 -2 \mathbf{d} \cdot \int_V \mathbf{r} \rho \,\mathrm{d}V. \end{align*}\end{split}\]

Here \(d^2 = \mathbf{d}\cdot\mathbf{d}\). The last integral in the last line of (5.16) is equal to the position of the center of mass, which we chose to be at the origin, so the last term vanishes, and we arrive at (5.15).

Note that the first two lines of Table 5.1 (moments of inertia of a stick) satisfy the perpendicular-axis theorem.

Theorem 5.2 (Perpendicular axis theorem)

If a rigid object lies entirely in a plane, and the moments of inertia around two perpendicular axes \(x\) and \(y\) in that plane are \(I_x\) and \(I_y\), respectively, then the moment of inertia around the axis \(z\) perpendicular to the plane and passing through the intersection point, is given by

(5.17)#\[ I_z = I_x + I_y. \]

Proof. We simply calculate the moment of inertia around the \(z\)-axis (where \(A\) is the area of the object, and \(\sigma\) the mass per unit area):

(5.18)#\[ I_z = \int_A (x^2 + y^2) \sigma \mathrm{d}A = \int_A x^2 \sigma \mathrm{d}A + \int_A y^2 \sigma \mathrm{d}A = I_y + I_x. \]

Note that the last two lines of Table 5.1 (moments of inertia of a thin planar rectangle) satisfy the parallel axis theorem.

../_images/c6q5_referenceframes.png

Fig. 5.1 Fernando Alonso racing on the circuit in Malaysia[3].#

5.5. Kinetic energy of rotation#

Naturally, a rotating object has kinetic energy - its parts are moving after all (even if they’re just rotating around a fixed axis). The total kinetic energy of rotation is simply the sum of the kinetic energies of all rotating parts, just like the total translational kinetic energy was the sum of the individual kinetic energies of the constituent particles in Section 4.5. Using that \(v = \omega r\), we can write for a discrete collection of particles:

(5.19)#\[ K_\mathrm{rot} = \sum_\alpha \frac12 m_\alpha v_\alpha^2 = \sum_\alpha \frac12 m_\alpha r_\alpha^2 \omega^2 = \frac12 I \omega^2, \]

by the  (5.13) of the moment of inertia \(I\). Analogously we find for a continuous object, using (5.14):

(5.20)#\[ K_\mathrm{rot} = \int_V \frac12 v^2 \rho \mathrm{d}V = \int_V \frac12 \omega^2 r^2 \rho \mathrm{d}V = \frac12 I \omega^2, \]

so we arrive at the general rule:

(5.21)#\[ K_\mathrm{rot} = \frac12 I \omega^2. \]

Naturally, the work-energy theorem (eq. (3.8)) still holds, so we can use it to calculate the work necessary to effect a change in rotational velocity, which by equation (5.12) can also be expressed in terms of the torque (in 2D):

(5.22)#\[ W = \Delta K_\mathrm{rot} = \frac12 I (\omega_\mathrm{final}^2 - \omega_\mathrm{initial}^2) = \int_{\theta_\mathrm{initial}}^{\theta_\mathrm{final}} \tau \mathrm{d}\theta. \]

5.6. Angular momentum#

In analogy with the definition of torque, \(\bm{\tau} = \bm{r} \times \bm{F}\) as the rotational counterpart of the force, we define the angular momentum \(\bm{L}\) as the rotational counterpart of momentum:

(5.23)#\[ \bm{L} = \bm{r} \times \bm{p}. \]

For a rigid body rotating around an axis of symmetry, the angular momentum is given by

(5.24)#\[ \bm{L} = I \bm{\omega}, \]

where \(I\) is the moment of inertia of the body with respect to the symmetry axis around which it rotates. Equation (5.24) also holds for a collection of particles rotating about a symmetry axis through their center of mass, as readily follows from (5.13) and (5.23). However, it does not hold in general, as in general, \(\bm{L}\) does not have to be parallel to \(\bm{\omega}\). For the general case, we need to consider a moment of inertia tensor \(\bm{I}\) (represented as a \(3 \times 3\) matrix) and write \(\bm{L} = \bm{I} \cdot \bm{\omega}\). We’ll consider this case in more detail in Section 7.3.

5.7. Conservation of angular momentum#

Given that the torque is the rotational analog of the force, and the angular momentum is that of the linear momentum, it will not come as a surprise that Newton’s second law of motion has a rotational counterpart that relates the net torque to the time derivative of the angular momentum. To see that this is true, we simply calculate that time derivative:

(5.25)#\[ \frac{\mathrm{d}\bm{L}}{\mathrm{d}t} = \frac{\mathrm{d}\bm{r}}{\mathrm{d}t} \times \bm{p} + \bm{r} \times \frac{\mathrm{d}\bm{p}}{\mathrm{d}t} = \bm{\tau}, \]

because \(\dot{\bm{r}} \times \bm{p} = \bm{v} \times m\bm{v} = 0\). Some texts even use equation (5.25) as the definition of torque and work from there. Note that in the case that there is no external torque, we arrive at another conservation law:

Theorem 5.3 (Law of conservation of angular momentum)

When no external torques act on a rotating object, its angular momentum is conserved.

Conservation of angular momentum is why a rolling hoop keeps rolling, and why a balancing a bicycle is relatively easy once you go fast enough.

What about collections of particles? Here things are a little more subtle. Writing \(\bm{L} = \sum_i \bm{L}_i\) and again taking the derivative, we arrive at

(5.26)#\[ \frac{\mathrm{d}\bm{L}}{\mathrm{d}t} = \sum_i \bm{r}_i \times \bm{F}_i = \sum_i \tau_i. \]

Now the sum on the right hand side of (5.26) includes both external torques exerted on the system, and internal torques exerted by the particles on each other. When we discussed conservation of linear momentum, the internal momenta all canceled pairwise because of Newton’s third law of motion. For torques this is not necessarily true, and we need the additional condition that the internal forces between two particles act along the line connecting those particles - then the internal torques are zero, and equation (5.25) holds for the collection as well. Consequently, if the net external torque is zero, angular momentum is again conserved.

../_images/billiardshots.svg

Fig. 5.2 Five types of billiard shots. (a-c) The type of motion depends on where the cue hits the ball. (a) If the cue hits the ball at exactly \(7R/5\) above the table, the ball will exhibit pure rolling motion, \(\omega = v R\). (b) If the cue hits the ball above the critical spot, it will rotate faster than translate (\(\omega > v R\)) and exhibit a slipping rotation. Friction will slow down the rotation and accelerate the translation until rolling motion is achieved. (c) If the cue hits the ball below the critical spot, it will translate faster than rotate (\(\omega < v R\)) and initially slide, until friction both slows down the translational speed and accelerates the rotational speed to the point where rolling motion is achieved. Note that the rotational motion may even be retrograde, i.e., backwards compared to the translational motion. (d-e) Behavior of the incident billiard ball before and after collision with a stationary ball of equal mass. Since the collision is elastic, all linear momentum is transferred to the other ball. If the incident ball was initially rolling, immediately after the collision it will continue rotating with complete slipping. Friction then causes the ball to pick up linear speed again, with a direction depending on the direction of the rotational motion, resulting in a follow (d) or draw (e) shot.#

5.8. Rolling and slipping motion#

When you slide an object over a surface (say, a book over a table), it will typically slow down quickly, due to frictional forces. When you do the same with a round object, like a water bottle, it may initially slide a little (especially if you push it hard), but will quickly start to rotate. You can easily check that when rotating, the object loses much less kinetic energy to work than when sliding - take the same water bottle, either on its bottom (sliding only) or on its side (a little sliding plus rolling), push it with the same initial force, and let go: the rolling bottle gets much further. However, somewhat ironically, the bottle can only roll thanks to friction. To start rolling, it needs to change its angular momentum, which requires a torque, which is provided by the frictional force acting on the bottle.

When a bottle (or ball, or any round object) rolls, the instantaneous speed of the point touching the surface over which it rolls is zero. Consequently, its rotational speed \(\omega\) and the translational speed of its center of rotation \(v_\mathrm{r}\) (where the r subscript is to indicate rolling) are related by \(v_\mathrm{r} = \omega R\), with \(R\) the relevant radius of our object. If the object’s center of rotation moves faster than \(v_\mathrm{r}\), the rotation can’t ‘keep up’, and the object slides over the surface. We call this type of motion slipping. Due to friction, objects undergoing slipping motion typically quickly slow down to \(v_\mathrm{r}\), at which point they roll without slipping.

Suppose we started our object with a velocity \(v_0\). If there is no rotation, the only force changing its velocity is the constant frictional force \(F_\mathrm{friction} = \mu_\mathrm{k} F_\mathrm{N} = \mu_\mathrm{k} m g\), with \(m\) the mass of the object (equation (2.13)). The constant force results in a linear decrease in the translational speed (see Section 2.3): \(v(t) = v_0 - \mu_\mathrm{k} g t\). However, if our object can roll, there is a second contribution to the motion, due to the torque \(\tau_\mathrm{friction} = F_\mathrm{friction} R\) of the frictional force. Using the rotational analog of Newton’s second law, equation (5.12) (or writing \(L = I \omega\) and using equation (5.25)), we get an equation of motion for the rotational velocity:

(5.27)#\[ I \alpha = I \frac{\mathrm{d}\omega}{\mathrm{d}t} = \tau_\mathrm{friction} = F_\mathrm{friction} R. \]

Integrating equation (5.27) with initial condition \(\omega(t=0) = 0\) we get \(\omega(t) = \mu_\mathrm{k} m g R t / I\). While the object undergoes slipping motion, the translational speed thus linearly decreases with time, whereas the rotational speed linearly increases. To find the time and velocity at which the object enters a purely rolling motion, we simply equate \(v(t)\) with \(\omega(t) R\), which gives

(5.28)#\[\begin{align*} t_\mathrm{r} &= \frac{v_0}{\mu_\mathrm{k} g (1 + m R^2 / I)}, \ \end{align*}\]
(5.29)#\[\begin{align*} v_\mathrm{r} &= \frac{v_0}{1+I/(m R^2)}. \end{align*}\]

Note that the time \(t_\mathrm{r}\) until fully rolling motion is achieved scales inversely with the friction coefficient, but the final rolling speed \(v_r\) is independent of the frictional force. The rolling speed does depend on the moment of inertia of your object - for a hollow cylinder it’s \(v_\mathrm{r} = \frac12 v_0\), whereas for a solid cylinder it’s \(v_\mathrm{r} = \frac23 v_0\). Once the object is rolling, its surface no longer moves with respect to the surface that it’s rolling on (as its instantaneous speed at the point of touching is zero). Consequently, the frictional force is much reduced, and the object can roll a large distance before it stops; in fact, the main force slowing it down once it is rolling is drag with the ambient air, which we could safely ignore when (kinetic) friction was still in the picture.

Example 5.1 (A cylinder rolling down a slope)

A massive cylinder with mass \(m\) and radius \(R\) rolls without slipping down a plane inclined at an angle \(\theta\). The coefficient of (static) friction between the cylinder and the plane is \(\mu\). Find the linear acceleration of the cylinder.

../_images/rollingcylinder_freebodydiagram.svg

Fig. 5.3 Free body diagram of a cylinder rolling down a plane.#

Solution There are at least three ways to tackle this problem. For all three, it helps (as always) to make a sketch, indicating the relevant forces - see Fig. 5.3.

  • Method 1: Forces and torques. Let the friction force \(F_\mathrm{f}\) be positive in the direction up the plane. Then we have:

    \[\begin{split}\begin{align*} F = ma \quad &\Rightarrow \quad mg \sin\theta - F_\mathrm{f} = m a \\ \tau = I \alpha \quad &\Rightarrow \quad F_\mathrm{f} R = \frac12 m R^2 \alpha \\ \text{no slipping} \quad &\Rightarrow \quad a = \alpha R. \end{align*}\end{split}\]

    The last two equations give \(F_\mathrm{f} = \frac12 m a\). Plugging this into the first equation gives

    \[a = \frac{g \sin\theta}{1 + \frac12} = \frac23 g \sin \theta.\]

  • Method 2: Energy. The total energy of the system is given by

    \[E_\mathrm{tot} = K + V = \frac12 m v^2 + \frac12 I \omega^2 + m g h.\]

    If the cylinder rolls down the slope without slipping, its angular and linear velocities are related through \(v = \omega R\). Also, if it moves a distance \(\Delta x\), its height decreases by \( \Delta x \cdot \sin \theta\). Conservation of energy then gives:

    \[\begin{split}\begin{align*} 0 &= \frac{\mathrm{d}E_\mathrm{tot}}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac12 m v^2 + \frac12 I \left(\frac{v}{R} \right)^2 - m g x \sin\theta \right]\\ &= m v \dot{v} + I \frac{v \dot{v}}{R^2} - m g v \sin\theta \\ &= \left[ a + \frac12 a - g \sin \theta \right] m v, \end{align*}\end{split}\]

    where we used \(I = \frac12 m R^2\) for a massive cylinder in the last line. The linear acceleration \(a\) is thus given by \(a = \frac23 g \sin\theta\).

  • Method 3: Rotational version of Newton’s second law. At a given point in time, we can apply the rotational version of Newton’s second law to rotations about the point where the cylinder touches the surface (as the cylinder is rolling without slipping, this is the only motion at that point). Of the three forces in the system, two act at that point, so they have no lever arm. Only gravity has a nonzero lever arm of length \(R \sin \theta\), leading to a torque given by \(\tau_z = m g R \sin\theta\). By the rotational version of Newton’s second law, we have \(\tau = I \alpha\), where \(I\) is the moment of inertia about the pivot. Applying the parallel-axis theorem, we find \(I = I_\mathrm{cm} + m d^2 = \frac32 m R^2\) in this case, so we get an angular acceleration of

    \[\alpha = \frac{\tau_z}{I} = \frac{m g R \sin\theta}{\frac32 m R^2} = \frac{2g}{3R} \sin \theta.\]

    The linear acceleration of the center of the cylinder due to the ‘rotation’ about this pivot is given by \(a = R \alpha = \frac23 g \sin\theta\).

5.9. Precession and nutation#

The action of a torque causes a change in angular momentum, as expressed by equation (5.25)). A special case arises when the torque is perpendicular to the angular momentum: in that case the change affects only the direction of the angular momentum vector, not its magnitude. Since the torque is given by the cross product of the arm and the force, this case arises when the angular momentum is parallel to either arm or force, or more generally, lies in the plane spanned by the force and arm. As a result, the angular momentum vector may start rotating about a fixed axis, a process known as precession. Due to the action of a second force (with associated torque), the angle between the angular momentum vector and the fixed axis (which we’ll call the \(z\)-axis) may also change, a process known as nutation.

../_images/Spinningtop.svg

Fig. 5.4 Precession of a spinning top. The top rotates about an axis which makes an angle \(\phi\) with the vertical (\(z\)) axis. The angular momentum of the top is parallel to the rotation vector. The arm between the pivot (where the top touches the supporting surface) and the center of mass is parallel to the angular momentum as well. Consequently, the torque of the gravitational force (which as always is pointed downward from the center of mass) is perpendicular to the angular momentum, and causes it to precess about the \(z\)-axis with a precession frequency \(\omega_\mathrm{p}\).#

The simplest example of a precessing system is that of a rotationally symmetric top, spinning about an axis that is not the vertical \(z\)-axis, see Fig. 5.4. In this case, the arm of gravitational force (pointing from the pivot at the origin to the center of mass of the top) is parallel to the angular momentum, which itself is parallel to the rotation vector, as \(\bm{L} = I \bm{\omega}\). The torque of gravity is thus perpendicular to the angular momentum. If we call the angle between \(\bm{L}\) and the \(z\)-axis \(\phi\), and work in cylindrical coordinates \((\rho, \theta, z)\), we can write \(\bm{L} = L_{xy} \bm{\hat{\rho}} + L_z \bm{\hat{z}}\), where \(L_{xy} = L \sin\phi\) is the projection of \(\bm{L}\) on the \(xy\)-plane, and \(\bm{\hat{\rho}}\) is the radial unit vector in the \(xy\)-plane (i.e., \(\bm{\hat{\rho}} = \cos\theta \bm{\hat{x}} + \sin\theta \bm{\hat{y}}\)). The gravitational torque is then given by:

(5.30)#\[ \bm{\tau}_\mathrm{z} = \bm{r} \times \bm{F}_\mathrm{z} = m g r \sin\phi \bm{\hat{\theta}}, \]

where \(\bm{r}\) is the arm pointing from the origin to the center of mass, \(r\) its length, and \(\bm{\hat{\theta}}\) the angular unit vector in the \(xy\)-plane (i.e., \(\bm{\hat{\theta}} = -\sin\theta \bm{\hat{x}} + \cos\theta \bm{\hat{y}}\)). For the time derivative of \(\bm{L}\), we get:

(5.31)#\[ \frac{\mathrm{d}\bm{L}}{\mathrm{d}t} = \frac{\mathrm{d}L_{xy}}{\mathrm{d}t} \bm{\hat{\rho}} + L_{xy} \dot{\theta} \bm{\hat{\theta}} + \frac{\mathrm{d}L_z}{\mathrm{d}t} \bm{\hat{z}}, \]

where we used (see equation (15.4))

\[ \frac{\mathrm{d}\bm{\hat{\rho}}}{\mathrm{d}t} = \frac{\mathrm{d}\bm{\hat{\rho}}}{\mathrm{d}\theta} \frac{\mathrm{d}\theta}{\mathrm{d}t} = \dot{\theta} \bm{\hat{\theta}}. \]

Equating (5.30) and (5.31), we find that \(\mathrm{d}L_{xy} / \mathrm{d}t = \mathrm{d}L_z / \mathrm{d}t = 0\), and

(5.32)#\[ \omega_\mathrm{p} \equiv \frac{\mathrm{d}\theta}{\mathrm{d}t} = \frac{m g r \sin\phi}{L_{xy}} = \frac{mgr}{I \omega}. \]

Equation (5.32) gives us the frequency of the precession about the \(z\)-axis. The associated precession rotation vector is given by \(\bm{\omega}_\mathrm{p} = \omega_\mathrm{p} \bm{\hat{z}}\).

Where precession, in terms of the angles used in this section, represents a change in \(\theta\), nutation is associated with a change in the tilt angle \(\phi\). It comes about in several cases, most commonly due to the action of a second force, and often results in a periodic motion (hence the name nutation, ‘nodding’). One example is the change in the Earth’s axis. As the axis is not perpendicular to the plane of Earth’s orbit (it presently makes an angle of about \(23.4^\circ\)), gravity from the sun exerts a net torque on the Earth’s rotation axis, causing it to precess with a period of about 25000 years. Consequently, the current polar star will only remain the polar star for a couple of centuries. Due to the torques exerted by the moon and the other planets, the Earth’s axis also nutates - with amplitudes from arcseconds to a few degrees, and periods that range widely, from 18.6 years due to the gravitational pull of the moon up to millennia due to other effects.

5.10. Problems#

Contents