6. Oxidoreduction

6.1. Oxidation/reduction reactions

One special category of transfer reactions are called reduction-oxidation reactions, or redox reactions. These reactions describe the transfer of electrons between chemical species. You have seen these reactions before in your basic chemistry course involving transfers of electrons between charged metal ions. For instance, iron (Fe) and copper (Cu) change their oxidation state when they gain and lose electrons:

\[\ {Fe}^{2 +}\ \ \ \leftrightharpoons \ {Fe}^{3 +} + \ e^{-}\]

Fe²⁺ is oxidized to Fe³⁺ (loses an electron)

\[{Cu}^{2 +} + \ e^{-} \leftrightharpoons \ \ \ \ \ \ \ {Cu}^{+}\]

Cu²⁺ is reduced to Cu⁺ (gains an electron).

The loss of an electron is a half-reaction called oxidation. It is always coupled with another chemical species gaining an electron, which is half-reaction called reduction.

The individual oxidation and reduction steps depicted above are half-reactions. What is meant by this? The loss of an electron from Fe²⁺ to generate Fe³⁺ (an oxidation) would not occur in isolation. That electron has to go somewhere! An oxidation reaction is therefore always coupled with a reduction reaction, and vice versa. Another way of saying this is that if a chemical species loses an electron in an oxidation, another chemical species must necessarily gain that electron as a reduction. Nevertheless, the half reactions depicted above are very useful concepts to keep in mind because different half reactions can be combined to make full redox reactions, as you will see later.

NEED TO KNOW

Redox reactions – or oxidoreduction reactions – describes the chemical reactions in which electrons are transferred between reactants. The net release of an electron occurs during oxidation; transfer of an electron to the product is called reduction.

How do we know we are looking at a redox reaction? Redox reactions are electron transfers, and in the simple context of Fe and Cu, the electron transfers are immediately obvious because electrons carrier a unit negative charge (-1); therefore, their gain or loss leads to a change in the formal charge of the ion. In most biochemical contexts, oxidation and reduction does not result in changing the formal charge of the molecule as we will see in the next section.

6.2. Redox reactions in organic compounds: what they look like

Applying redox terminology to organic compounds is not quite as obvious as compared to metal ions changing formal charge. This is because most molecules are organic carbon compounds that share electron pairs and that therefore do not have a formal charge. Redox reactions involving organic molecules focus upon the oxidation state of the carbon atoms involved in the reaction. How to determine the oxidation state? The carbon atoms within an organic molecule are most often bound to H, C, S, N, or O. The oxidation state of a carbon atom is determined by the number of bonds made to an atom that is more electronegative than carbon. When carbon shares electrons with an atom that is more electronegative (such as O), the electrons within the C-O covalent bond(s) will tend to dwell around the oxygen more than they dwell around the carbon. Moving up the scale of electronegativity, with H being the least electronegative and O being the most electronegative, each step increases the oxidation state of the carbon. This scale of carbon oxidation from most reduced (top) to most oxidized (bottom) is depicted in Fig. 6.1:

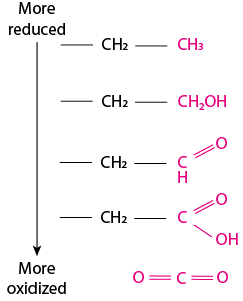
Fig. 6.1 . An oxidation-reduction scale for organic compounds. The carbon colored in pink begins with the most reduced in the table at the top (an alkane, three bonds to H and one bond to C) and then becomes increasingly oxidized: the first step makes an alcohol (one bond to oxygen), next, two bonds to oxygen (aldehyde), next, three bonds (carboxylic acid), finally, four bonds (carbon dioxide). Note that it is possible to be more reduced than the alkane at the top of the table: methane (CH₄) has four bonds to H, which is less electronegative than carbon.

Note that the explanation above is one specific case of oxidation-reduction reactions. It can be confusing that “oxidation” sounds like “oxygen” when in fact carbon can be oxidized by making a bond with nitrogen, or that converting an alkane to an alkene (introducing a carbon-carbon double bond) is also considered an oxidation. Furthermore, a carbon-fluorine bond would be considered “more oxidized” than a carbon-oxygen bond because fluorine is more electronegative than oxygen. It is more accurate to speak in terms of changes in oxidation: a carbon atom becomes more oxidized after an increase in the average electronegativity of atoms covalently bound to it. Less-obvious oxidation-reduction reactions are shown in Fig. 6.2. Moving from left to right, the carbons are becoming more oxidized because the electronegativity of atoms bound to carbon in each case is increasing (carbon is more electronegative than hydrogen).

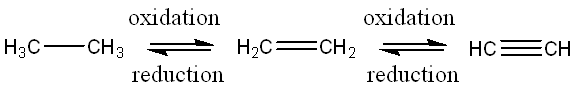
Fig. 6.2 . Less-obvious oxidation/reduction reactions. The carbons in the alkane on the left become oxidized by the introduction of a C-C double bond because the carbons are making a bond to an atom more electronegative than H.

Keeping the difference of electronegativity in mind, let’s have a closer look at each electron couples that the pink carbon atoms in Fig. 6.3 share with each of their neighboring atoms. Each carbon will share four couples of electrons in total; for each of these shared e^- couples, if the carbon is most electronegative, they are colored in blue. The couple of electrons shared between a carbon and a more electronegative atom are colored in black. As the carbon shares more and more electrons with electronegative atoms, these electrons tend to be closer to the electronegative atom more and more:

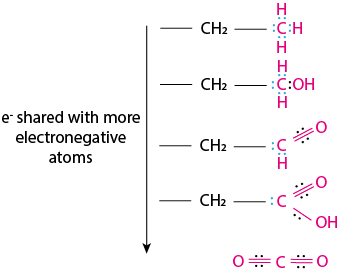
Fig. 6.3 Electronic configuration of a carbon in progressively reduced compounds.

6.3. Biological redox reactions and electron carriers

Most biological redox reactions look different from those involving metal ions. There is (often) no clear exchange of entire electrons and no gaining or losing formal electrostatic charge in the process. Let’s look at an example of a biological redox reaction in more detail to see these differences.

The following half-reaction is catalyzed by lactate dehydrogenase:

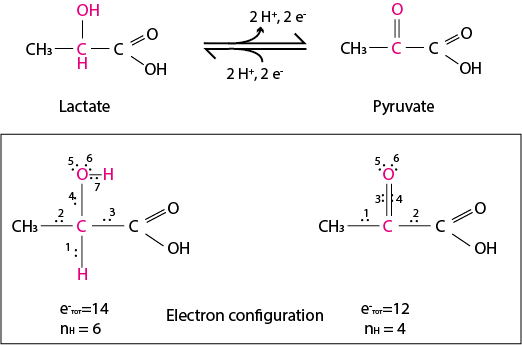
Fig. 6.4 Half-reaction showing the oxidation of lactate to pyruvate, and the reduction of pyruvate to lactate. In the electron configuration it can be seen that the central carbon “loses” two electrons because they are now shared with an oxygen instead of a hydrogen.

In this half-reaction, lactate is oxidized to pyruvate. The central carbon of pyruvate shares one more bond (single to double) than lactate with a more electronegative atom (O). Counting the electron couples shared by the atoms involved this reaction, depicted in the electron configuration panel of Fig. 6.4, it clearly emerges how the central carbon of lactate has “lost” the electron couple (couple n^o 1) that it used to share with the H atom, which is now released as proton, H⁺. Conversely, pyruvate is reduced to lactate by receiving two electrons and a proton at its central carbon. As the central carbon of pyruvate loses the double bond to a very electronegative atom (O), it has “gained” the electron couple from the newly-introduced H. Note that the total number of bonds does not change!

When a half-reaction is written as Fig. 6.4, the electrons exchanged are graphically represented as they were released as protons (H⁺) and electrons (e^-). However, in the aqueous environment of a cell, free electrons and free protons are never spontaneously released into solution in this way. Instead, they are transferred directly to electron acceptors or are received directly from electron donors. Many enzymatic reactions use specific cofactors known as electron carriers.

NEED TO KNOW

Electrons released by redox reactions are not released in the surroundings uncontrolled, but are taken up by molecules which function is to receive these electrons and act as electron carriers.

Which molecules receive the electrons from lactate?

6.4. Soluble cofactors NADH and NADPH serve as electron carriers

The main biological electron carriers are nicotinamide adenine dinucleotide (abbreviated in its oxidized and reduced form as NAD+ and NADH, respectively) and nicotinamide adenine dinucleotide phosphate (NADP+ and NADPH for oxidized and reduced forms, respectively). These are collectively referred to as NAD(P)+ and NAD(P)H. While it may seem redundant to have two different electron carriers that are so structurally similar, it is essential to notate that the two carriers are not interchangeable. Reasons for having two different electron carriers will become apparent later on.

Electrons are transferred between NAD(P)H and substrates as a hydride ion (H^-, or a proton with two electrons), with a proton (H⁺) being exchanged with the solution. The part of NAD(P)H that exchanges the hydride ion are highlighted in the cyan boxes in Fig. 6.5:

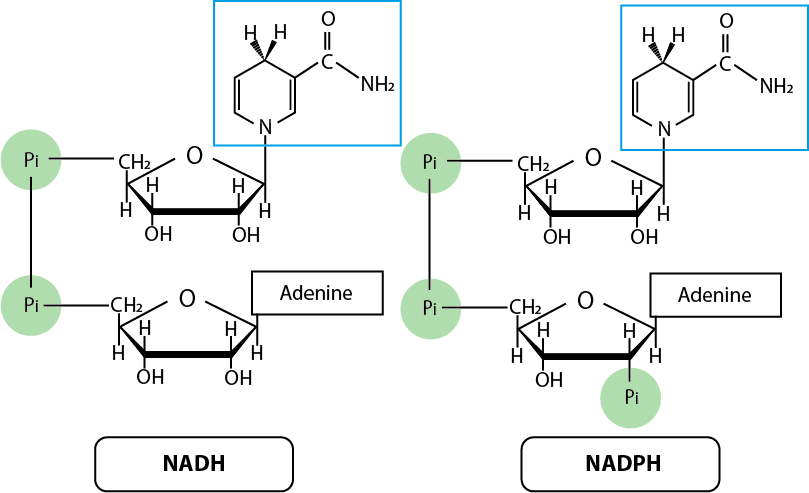
Fig. 6.5 NADH and NADPH

Fig. 6.6 illustrates how electrons are taken up by NAD⁺ and NADP⁺ in the form of a hydride ion:

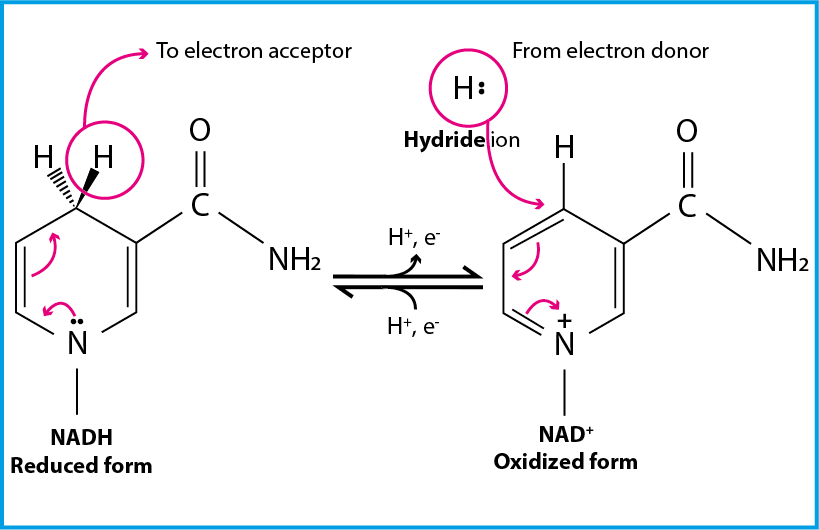
Fig. 6.6 The reactive group of either NADH or NADPH is based on accepting a hydride ion and distribute the negative charge that this introduces on the tertiary amine within the ring.

6.5. Thermodynamics of redox reactions

Will a redox reaction happen in a given condition? Let’s consider lactate oxidation to pyruvate with NAD+ as the redox partner:

Lactate + NAD⁺ 🡪 pyruvate + NADH

Like all chemical reactions, this reaction may be either thermodynamically favorable (meaning more products will be produced over time) or unfavorable (meaning more reactants will be produced over time). As you recall, whether this reaction will tend to generate more lactate and NAD+ or more pyruvate and NADH depends upon \(\Delta G\), which itself is determined by both the free energy of the reaction in standard free conditions (\(\Delta G'^{\circ}\)) and the relative concentrations of reactants and products (the mass action term). How can we do a similar prediction for redox reactions? How can we calculate the thermodynamic favorability of a redox reaction?

NEED TO KNOW

Electrons spontaneously move from compounds with low reduction potential compounds (which have relatively low affinity for electrons) to compounds with high reduction potentials (which have relatively high affinity for electrons).

Calculating the reduction potential of the reactants of a redox reaction is key to understand its thermodynamics. Use the Nernst equation to calculate the reduction potential for a give redox reaction:

(6.1)\[E = \ E^{0} + \frac{RT}{nF}\ln\frac{\lbrack electron\ acceptor\rbrack}{\lbrack electron\ donor\rbrack}\]

Where:

\(E\) = half-cell reduction potential

\(E^0\) = standard half-cell reduction potential

\(R\) = gas constant, in J/K*mol

\(T\) = temperature in Kelvin

\(n\) = number of electrons exchanged in the reaction

\(F\) = Faraday constant, the total value of charge (in Coulombs) in 1 mole of e^-. Converted to kilojoules per volt, \(F\) = 96.5 kJ/V*mol^-1.

How do we calculate \(E^0\)? \(E^0\), the standard reduction potential, is defined in terms of half reactions. Unlike for \(\Delta G\), which indicates a spontaneous (favorable) reaction when \(\Delta G < 0\), a redox reaction is spontaneous (favorable) when \(\Delta E > 0\).

As mentioned earlier, all redox reactions can be broken down into two half reactions: the oxidation (loss of an electron) from the electron donor and the reduction (gain of an electron) to the electron acceptor. The potential difference between the two compounds defines the value of \(E^0\), the standard reduction potential.

\(E^0\) is the difference between the reduction potential of the electron acceptor and the reduction potential of the electron donor (Equation (6.2)):

(6.2)\[{\mathrm{\Delta}E}^{'0} = E_{acceptor}^{'0} - \ E_{donor}^{'0}\]

A positive \(\Delta E\) indicates that the acceptor potential for receiving electrons is higher than the donor potential for accepting electrons. In these conditions, the reaction is evidently favorable and spontaneous.

Table 6.1 Standard reduction potential of biologically relevant half-reactions at neutral pH (pH = 7).

Description	Half-reaction	\(\Delta E'^{\circ}\) (V)
Reduction of oxygen	\(\frac{1}{2}\) O2 + 2H+ + 2e- \(\rightarrow\) H2O	0.816
Reduction of ferric ion	Fe3+ + e- \(\rightarrow\) Fe2+	0.771
Reduction of nitrite ion	NO3- + 2H+ + 2e- 🡪 NO2- + H2O	0.421
Reduction of pyruvate	Pyruvate + 2H+ + 2e- 🡪 Lactate	-0.185
Reduction of acetaldehyde	Acetaldehyde + 2H+ + 2e- 🡪 Ethanol	-0.197
Reduction of NAD+	NAD+ + H+ + 2e- 🡪 NADH	-0.320
Reduction of NADP+	NADP+ + H+ + 2e- 🡪 NADPH	-0.324

Reduction potentials can be related to free energy changes:

(6.3)\[{\mathrm{\Delta}G}^{'0} = - n\ F\ {\mathrm{\Delta}E}^{'0} \text{ or } \mathrm{\Delta}G = - n\ F\mathrm{\Delta}E,\]

where

\(n\) = number of electrons exchanged in the reaction

\(F\) = Faraday constant

A reaction with positive \(\Delta E\) will therefore be characterized by negative \(\Delta G\), and therefore will be spontaneous.

How do we use Table 6.1 to calculate \(\Delta E'^{\circ}\)? This can get a little bit confusing. Let’s use lactate oxidation as an example:

Lactate + NAD⁺ 🡪 pyruvate + NADH

The first step is to identify the electron donor and the electron acceptor in the reaction. You can figure this out either by comparing the chemical structures of lactate and pyruvate, which will show you that pyruvate has one more bond between a carbon and an oxygen than lactate, which means that lactate was oxidized and was therefore the electron donor. An easier way than counting bonds is to simply remember that NAD⁺ is always an electron acceptor, which would necessarily mean that lactate must be an electron donor. (Similarly, NADH is always an electron acceptor.)

We’ve identified the electron acceptor (NAD⁺) and the electron donor (lactate). Now we plug the values in Table 6.1 of the half-reaction reduction potentials and use Equation (6.2) to calculate the reduction potential of the overall reaction (\(E_\text{acceptor}-E_\text{donor}\)). From the table, we see that the reduction of NAD⁺ is -0.320 V. The reaction involving the oxidation of lactate is not depicted; however, the reverse reaction (reduction of pyruvate) is given: -0.185 V. Now we plug this into Equation (6.2) without changing the signs of the values: (\(E_\text{acceptor}-E_\text{donor}\)) = (-0.320 V – (-0.185 V)) = -0.135 V. So in standard conditions (1 M products and reactants, pH 7), the oxidation of lactate to pyruvate by NAD⁺ is unfavorable because \(\Delta E'^{\circ}\) is negative.

So we have \(\Delta E'^{\circ}\). Now how do we calculate \(\Delta G'^{\circ}\)? Equation (6.2) is quite straightforward; however sometimes there is confusion about the number of electrons involved (\(n\)). For the oxidation of pyruvate, there are 2 electrons involved (see Table 6.1 for both reactions), so \(n=2\). Finishing the calculation:

ΔGʹ⁰ = -2*96.5 kJ/V*mol^-1 *(-0.135 V)

ΔGʹ⁰ = +26.1 kJ/mol

From standard conditions (where reactant and product concentrations are all = 1 M), this reaction will tend to reduce pyruvate to lactate, instead of oxidizing lactate to pyruvate.

6.6. Electron transfers can drive ATP production

If there are strong oxidants available, NADH oxidation can be directed towards ATP generation. Calculating free energy for reduction potential enables us to understand how the cell can use the potential energy in redox reaction to generate chemical energy for its needs in the form of ATP. This is the key function of electron transport chain.

How much electric potential (measured in V) does the hydrolysis of one ATP to ADP and Pi release?

By incorporating the \(\Delta G'^{\circ}\) of ATP hydrolysis into Reaction 6.2 to calculate the electrical energy associated with the free energy released by ATP in standard conditions (-30.5 kJ/mol) we find that:

ATP 🡪 ADP + P_i is equivalent to +0.316 V/mol per electron.

Which means that any redox reduction where ONE electron transfer equals this energy or more has the potential to generate one ATP molecule. Using this number, we can compare the energy generated by the transfer of electrons from NADH to O₂ (respiration) against the energy generated by the transfer of electrons from NADH to pyruvate (fermentation). This table also implies the existence of alternative electron acceptors such as nitrite (NO₃^-). Humans cannot use nitrite as an electron acceptor. However, many bacteria do use nitrite as an electron acceptor when oxygen is not available.

NADH is not the only electron carrier present in the cell. Other molecules are used as electron carriers, but also, there are other uses for electron carriers other than pumping electrons into the electron transport chain to generate ATP. One other electron carrier that is almost chemically identical (and which reduction potential is also very similar) to NADH, is called NADPH. The difference is the present of a phosphate group in the place of the 2’ hydroxyl (see Fig. 6.5). The phosphate group in this position is never directly involved in a redox reaction and does not significantly change the reduction potential, but it serves the purpose of allowing enzymes to distinguish the two carriers. This occurs because enzymes which active site requires NADPH are able to avoid binding NADH due to the presence or absence of the phosphate group.

GOOD TO KNOW

The presence of multiple electron carrier pathways in the cell allow the presence of. The existence of multiples carriers allows the cell to de-couple pathways that need redox reactions to be driven in different direction between each other. This is achieved by keeping the concentration of the oxidized and the reduced forms in dramatically different ratios per each redox couples (even if they have with similar reduction potential!)

The directionality of a pathway can be enforced by maintaining a specific ratio between concentrations of electron acceptor and electron donor, as from the Nernst equation.