5. Bioenergetics#
5.1. When catalysis is not enough#
You have learned in Chapter 3 how enzymes catalyze the chemical reactions that convert basic nutrients into the building blocks of living biomass, and in Chapter 4 how these chemical reactions are controlled and balanced to ensure that the building blocks are supplied in the right proportions to sustain life. However, for many reactions, a catalyst is not sufficient on its own to generate products from substrates. As you remember from your lectures on chemical thermodynamics, chemical reactions may be either thermodynamically favorable or thermodynamically unfavorable. Thermodynamically favorable reactions will end up with more products than reactants once equilibrium is reached, while unfavorable reactions will always end up with fewer products than reactants. Since all chemical compositions (concentrations of reactants and products) that are out of equilibrium will always change in the direction of reaching equilibrium, the fact that some chemical reactions essential for life are unfavorable is rather inconvenient.
This is important because as you recall, catalysts (including enzymes) cannot change the thermodynamic favorability of any chemical reaction. All catalysts can do is lower the transition state between reactants and products, which greatly decreases the time required to reach equilibrium. So if the equilibrium ratio of products to reactants (\(P/R\)) is 100 (so 100 molecules of product per reactant molecule) then a catalyst will be sufficient to generate this 100:1 ratio in a short amount of time. However, if the equilibrium ratio is reversed and the \(P/R\) ratio is 0.01 (so only 1 molecule of product is generated per 100 molecules of reactants at equilibrium) then a catalyst will only be able to convert a tiny proportion of reactants into product. For many reactions in metabolism, this is unworkable because many more molecules of product are required to sustain a living cell.
Many reactions in metabolism (but not all) are thermodynamically unfavorable and will not generate sufficient product if left on their own, much like a car will never spontaneously roll from the bottom to the top of a hill. These unfavorable reactions therefore require an input of chemical energy that causes the reaction to become favorable, just like the energy released from petrol combustion can be harnessed by an engine to drive a car from the bottom to the top of a hill. As you’ve likely learned from basic biology classes, one of the substances analogous to petrol that allows unfavorable reactions to take place is adenosine triphosphate (ATP). However, it is not obvious how enzymes use ATP and other so-called “high energy compounds” to obtain the products of unfavorable reactions. How do enzymes harness chemical energy to generate products from reactants?
In this chapter, we will focus on all the things energetic in the cell.
A review of chemical thermodynamics
The additivity of free energies in a metabolic pathway
How enzymes use ATP to “drive” unfavorable chemical reactions
Induced fit theory, or how enzyme structures channel chemical energy
5.2. Equilibrium and concentrations: an intuitively-accessible explanation from the perspective of single molecules#
Look at the following reactions:
These reactions involve the same molecules but run in opposite directions. If I have an aqueous mixture of ATP, ADP, and phosphate, which one of the two reactions is more likely to happen? Since these two reactions are simply the same reaction run in opposite directions, another way of asking this question is simply: what will be the concentrations of reactants and products once these reactions reach equilibrium?
The answer to this question is determined by the relative stability of reactants and products. There are different ways to think about this, but perhaps the most straightforward way is to start with probability. In the presence of a catalyst (such as an enzyme), products and reactants freely interconvert with each other. The probabilities of interconversions determines the concentration of reactants and products at equilibrium. For instance, imagine a reaction for which the equilibrium ratio of products to reactants is 1/1. This means that if you start with 100 molecules of either reactant or product and allow the molecules to approach equilibrium, you will get 50 molecules of both at the end. What does this equilibrium look like from the perspective of individual molecules?
Reactant molecules all have the same likelihood of spontaneously turning into a product molecule. To illustrate with an example, let’s give this likelihood a number: say, every individual reactant molecule has a 10% chance every second of becoming product. Meanwhile, the product molecules also have some probability of converting back into reactant. Because the equilibrium ratio of products to reactants is 1:1, we know the probability of the reverse reactions: every product molecule has the same chance of becoming reactant as the reactants have of turning into products. So if every reactant molecule has a 10% chance of becoming product every second, then at equilibrium where we have 50 molecules of product and 50 molecules of reactant, then 5 reactant molecules (10% of 50 reactant molecules) will turn into product. This would mean that we’d have 45 molecules of reactant and 55 molecules of product. However, the concentration ratio does not become 45/55, because in parallel with the spontaneous conversion of reactant to product, on average 5 molecules of product (10% of 50 product molecules) will spontaneously turn back into reactant. Thus, the equilibrium value of 50/50 is maintained.
There are very few chemical equilibria where the ratio of products to reactants is 1:1. What about something more realistic, such as a product/reactant ratio of 9/1? In this case, once we reach equilibrium from 100 molecules of either product or reactant, we’d have 10 molecules of reactants and 90 molecules of product. Let’s consider this from the standpoint of individual molecules and impose the same probability of reactant to product conversion as in the previous example: each reactant molecule has a 10% chance per second of turning into product. This means that at equilibrium, every second, on average 10% of 10 molecules (1 molecule) are turning into product.
What is the probability of products converting back to reactants? Conveniently, this probability can be obtained from the thermodynamic equilibrium ratio between products and reactants. It turns out that the ratio of conversion probabilities is identical to the equilibrium ratio. If the ratio of products to reactants is 9:1, then the ratio of the rates of interconversion is also 9:1. This means that the probability of conversion of product back to reactant is 1/9th the probability of conversion of reactant to product. Thus, to obtain the probability per second of back conversion from product to reactant, we divide the 10% per second of reactant to product by 9, which gives us a ~1.11% chance that any given product molecule will turn back into reactant.
How do these probabilities lead to the equilibrium ratio of 10 molecules of reactant to 90 molecules of product? Remember that if 10% of reactant molecules are spontaneously converting to product every second, that means that on average 1 molecule (10% of 10 molecules) are converting every second. From the product side, the probability of a given product molecule converting back to reactant is 1.11%. 1.11% of 90 molecules is ~1 molecule converting back to reactant every second on average. So once again, we have 1 molecule of reactant turning into product that is exactly balanced out by 1 molecule of product turning back into reactant. Thus, the equilibrium value (products/reactants) of 90/10 maintained.
This previous example illustrates the most important aspect of equilibrium: at equilibrium, the number of interconversions between products and reactants are equal, even when the concentrations of reactants and products are not equal. As a consequence, there is no net change in product and reactant concentrations.
Let’s look at that last statement again and expand on how the number of interconversions between products and reactants become equal at equilibrium. If we have only 10 reactant molecules left at equilibrium and we are losing 1 reactant per second to the product pool, why do we nevertheless always have 10 reactants? And how do we still have 10 reactants when each product molecule has only a 1.11% chance to convert back to reactant? The answer is that the equilibrium ratio is maintained despite the differences in probabilities because the size of the product pool at equilibrium is so much larger (9 times) than the reactant pool. While any individual product molecule is 9 times less likely to convert to reactant than any individual reactant molecule will convert to product, because there are 9 times more product molecules, the overall probability of one product -> reactant conversion per second is identical to the overall probability of one reactant -> product conversion per second. This is chemical equilibrium.
What about being out of equilibrium? Why do all non-equilibrium concentrations approach the equilibrium concentration? Again, think about probabilities above where the equilibrium ratio of products to reactants at is 9:1. Imagine we have an out-of-equilibrium 50:50 mix of products and reactants. How does this 50:50 mix inevitably approach a 90:10 ratio of products and reactants? Let’s calculate the number of conversions per second once again: each reactant molecule has a 10% chance of converting per second, so 10% of 50 reactants is (on average) 5 molecules going to product every second. In the other direction, we have each product molecule having a 1.11% chance of converting. 1.11% of 50 is 0.55 molecules per second (equivalent to about 1 molecule every 2 seconds). So on average there are many more reactant to product conversions happening in this out-of-equilibrium situation than there are product to reactant conversions. This imbalance remains until we reach the equilibrium ratio of 9 products to 1 reactant. At this equilibrium concentration, the number of interconversions between reactants and products per unit time are equal, as described above. This is why reactions always approach equilibrium from any arbitrary starting condition.
And now we can start thinking about equilibrium constants. The thermodynamic favorability of a reaction is expressed by the equilibrium constant \(K_\text{eq}\), which is the ratio of products to reactants (\(P/R\)). We can then calculate the standard free energy released \(\Delta G'^\circ\) as equilibrium is approached from a standard condition (defined in the next page), and from there, calculate the free energy released as equilibrium is approached from any arbitrary condition.
Reaction (5.1) can be rewritten in terms of generic chemical species (uppercase letters) and ratios (lowercase letters):
We can infer energy (released or absorbed) from the (measured) ratio of concentrations of products and reactants at equilibrium. This ratio is \(K_\text{eq}\), the ratio between concentrations of products, each raised to the power of their coefficient in the equation and the concentration of the substrates raised to the power of their coefficient in the equation:
Which, when applied to reaction (5.1) (and after removing the concentration of water, which is neglected in reported \(K_\text{eq}\) values for biochemical reactions), becomes:
In this case, there are many more product molecules (ADP and phosphate) than reactant molecules (ATP) at equilibrium. ATP is much more likely to break into ADP and phosphate than ADP and phosphate are likely to spontaneously reform ATP.
It is possible to calculate the ratio of ATP to ADP and phosphate at equilibrium: if ADP and phosphate concentrations are equal, then there will be about 470 times more ADP than ATP, or one molecule of ATP per 470 molecules of ADP.
5.3. Gibbs free energy#
But what determines these probabilities? Why is ADP and phosphate more stable than ATP? This has to do with the relative stability of the chemical bonds in the reactants and products. We’ll discuss this briefly below.
We determine energies from the (measured) ratio \(K_\text{eq}\) of concentrations of products and reactants at equilibrium. In the case of ATP and ADP, we would infer that the balance of reactants to products strongly favors production of ADP and phosphate over ATP. As the reaction proceeds, the concentrations of the molecules involved change in favor of the products: the equilibrium constant represents the value of concentration ratio between products and reactants at equilibrium. Once the balance reaches this equilibrium, the reaction stops, because reactions always proceed towards equilibrium concentrations. As described above, although interconversions between products and reactants may still be occurring, at equilibrium these interconversions exactly balance out so there are no net changes in concentration.
What is the relationship between chemical equilibrium and Gibbs free energy?
Equation (5.3) shows the standard Gibbs energy change, where
\(\Delta G'^\circ\) = standard Gibbs energy change
\(R\) = gas constant = 8.314 J/K*mol
\(T\) = temperature in Kelvin
\(K_\text{eq}\) = thermodynamic equilibrium constant
The standard Gibbs free energy, \(\Delta G'^\circ\) is a reference value defined as the energy released when all reactants and products are present in solution at a concentration of 1 M and are allowed to reach equilibrium concentrations in standard conditions: 298 K, pH 7.0, 1 atmosphere of pressure. For reaction (5.1):
\(K_\text{eq}\) is ~ 2.2 x 105 M. When introduced into Equation (5.3), the natural logarithm of this \(K_\text{eq}\) value (\(ln(K_\text{eq})\)) will yield a positive number multiplied by \(-RT\). As a consequence, the value of \(\Delta G'^\circ\) of reaction (5.1) will be negative : the standard conditions will generate products, ADP and phosphate, as the reaction approaches equilibrium.
What about thermodynamically unfavorable reactions? For those reactions, there will be more reactants than products at equilibrium. This means that the ratio of products to reactants \(K_\text{eq}\) will be less than 1. When introduced into equation (5.3), the natural logarithm of any number less than 1 will be negative. Multiplied by \(-RT\), we will obtain a positive \(\Delta G'^\circ\) value: meaning that the reaction will produce more reactants when initiated from standard conditions where reactant and product concentrations are equal.
This definition of standard free energy is helpful to understand how the direction of a reaction, and the energy released, depends upon the starting concentrations of products and reactants. Standard free energy is a useful parameter to compare various reactions and is essential for calculating the thermodynamic favorability of reactions regardless of whether concentrations match the standard reference condition of 1 M.

The equilibrium constant \(K_\text{eq}\) can be also calculated from \(\Delta G'^\circ\):
For standard biochemical conditions:
\(T\) = 298 Kelvin (25°C)
\(RT\) = 2.478 kJ/mol.
5.4. Calculating equilibrium constants and standard Gibbs free energies of reverse reactions from forward reaction values#
An important point about reaction reversibility. The reversibility of chemical reactions is incredibly important in biochemistry. However, students are often taught that there is a distinction between reversible and irreversible reactions. This distinction is untrue and contributes to confusion because all reactions are (in theory) reversible. The reactions that you encounter in your everyday life that are presented as examples as “irreversible” reactions are, in fact, theoretically reversible – but in reality, the chances that carbon dioxide and water will spontaneously recombine into petrol are so incredibly low that petrol combustion is effectively irreversible. However, petrol combustion and (for instance) the isomerization of glucose-6-phosphate and fructose-6-phosphate are both theoretically-reversible chemical reactions and only differ in the degree of reversibility: petrol combustion is effectively irreversible (we will never see carbon dioxide and water recombine to generate gasoline in normal conditions) while the isomerization of glucose-6-phosphate and fructose-6-phosphate is highly reversible (these isomers rapidly interconvert many times per second in the presence of a catalyst).
For a reaction \(A\rightarrow B\) with equilibrium constant \(K_{\text{eq}, A\rightarrow B}\), the equilibrium constant \(K_{\text{eq}, B\rightarrow A}\) of the reverse reaction \(B\rightarrow A\) will always be the inverse of the forward equilibrium constant: (\(1/K_{\text{eq}, A\rightarrow B}\)). This is straightforward to understand because the equilibrium constant for the forward reaction \(K_{\text{eq}, A\rightarrow B}\) is product concentration divided by reactant concentration at equilibrium: \(B/A\). Reversing the direction of the reaction means that we have designated \(B\) as the reactant and \(A\) as the product, so the equilibrium constant for the reverse reaction \(K_{\text{eq}, A\rightarrow B}\) is simply \(A/B\).
For the standard Gibbs free energy \(\Delta G'^\circ\) for \(A\rightarrow B\), \(\Delta G'^\circ\) of \(B\rightarrow A\) will simply be (\(-1 \cdot \Delta G'^\circ\)).
Illustrating this with ATP hydrolysis:
The reverse reaction (ATP formation from ADP and phosphate) is (\(-1 \cdot \Delta G'^\circ\)) = -1*(-30.5 kJ/mol):
5.5. Components of Gibbs free energy#
Gibbs free energy can be decomposed into enthalpy and entropy terms:
where
\(\Delta_r G'^\circ\) = standard Gibbs energy change
\(\Delta H\) = enthalpy change of the system
\(T\) = temperature in Kelvin
\(\Delta S\) = entropy change of the system
For a spontaneous reaction:
Therefore:
Enthalpy is simply the heat released by a chemical reaction. In terms of chemical bonds, the heat release reflects the difference in energy between the bonds present in the reactants and the products. A fuller discussion of which bonds release more or less heat is beyond the scope of a short biochemistry textbook.
Entropy is considerably more complicated to think about in condensed-phase systems like a living cell. If you want to think about how the arrangement of molecules relates to entropy, attempting to calculate the entropy of a solution of sodium chloride relative to undissolved salt crystals sitting in water is surprisingly difficult! Relating entropy to disorder is not often helpful either. But you can think about entropy as the number of molecular arrangements that result in a particular property. A better explanation will be provided in your statistical mechanics course!
5.6. How concentrations of reactants and products determine thermodynamic favorability#
Remember: equation (5.3) defines \(\Delta G'^\circ\), the standard Gibbs energy change, as a reference value that defines the energy released in standard conditions, when all reactants and products start at 1 M concentration, at 25°C and pH 7, and move towards the concentration ratios that exist at equilibrium. While temperature and pH of the standard conditions are reasonably close to a living cell, a concentration of 1 M of any molecule is extremely high and likely impossible for most metabolites. Therefore, this reference concentration (1 M) is never actually observed in living cells. The most abundant metabolite in E. coli (glutamate) is 300 mM, while most metabolites are less than 1 mM. Thus, for nearly all reactions, the \(\Delta G'^\circ\) alone does not determine whether a reaction is favorable.
We therefore need to calculate the actual Gibbs free energy change for the concentrations that appear. The Gibbs free energy change is defined as:
where \([C]\) and \([D]\) are products, and \([A]\) and \([B]\) are reactants (exponents indicate stoichiometry of each chemical species). Equation 2 is used to calculate the \(\Delta G\) of a given reaction in any desired conditions of temperature and reactant concentrations. The mass-action ratio (the products/reactants concentration ratio in red) is just as relevant to determining the free energy change (and thus reaction favorability) as the \(\Delta G'^\circ\) value. Note that from Equations (5.3) and (5.4), when [products]/[reactants] ratio reaches its equilibrium concentration \(K_\text{eq}\), then
Unlike \(\Delta G'^\circ\), \(\Delta G\) takes into account the concentrations of reactants and products in real conditions, which actually tells us whether a reaction will proceed to generate more products than reactants. Even for reactions that are unfavorable in the standard reference condition (for which \(\Delta G'^\circ\) is positive and \(K_eq\) is < 1), a high concentration of reactants will mean that \(\Delta G\) becomes negative and thus very favorable. We’ll explore this further in the next section on Le Chatelier’s Principle.
Exercise 5.1
Intracellular concentration of ATP ranges between 2-4 mM, with peaks of 5-6 mM in metabolically active cell types like muscles (Greiner and Glonek 2021). Let’s consider a cell with [ATP]= 2.5 mM, [ADP] = 0.25 mM, [Pi] = 1.7 mM.
In the cellular conditions where the reagents concentrations are as described above, will ATP or ADP be spontaneously produced? Which of the reactions below is spontaneous?
Solution to Exercise 5.1
For Reaction (5.1):
ΔG = -30.5 kJ/mol + 2.478*ln(0.00017) kJ/mol = -52.0 kJ/mol released (at T = 25 oC) when reaction moves towards equilibrium. Equilibrium favours ADP production.
5.7. Le Chatelier’s Principle, or how seemingly-unfavorable reactions can generate more products than reactants without the help of ATP#
How can changes in concentration make reactions that are unfavorable in the standard reference condition become favorable? The answer is that in many cases, cellular metabolism maintains the ratio of reactant metabolites to product metabolites in a range that is far from the equilibrium value. This ratio will always spontaneously move towards equilibrium due to a greater number of conversions from reactant to product than conversions from product to reactant. This is an aspect of Le Chatelier’s principle: when a chemical solution is perturbed away from equilibrium concentrations (such as by product concentrations decreasing due to a downstream reaction), the concentrations within the solution will spontaneously change to restore the equilibrium. This spontaneous change does not directly require any energetic input. Cellular metabolism takes advantage of this principle by driving some unfavorable reactions without any coupling with an external source of chemical energy such as ATP.
Let’s illustrate this principle by looking at the first step of glycolysis, the pathway that produces energy in form of ATP from glucose:
The net change of free energy associated with this reaction is positive, which means that when initiated from standard conditions with G6P and F6P concentrations set at 1 M, this reaction will tend to generate reactants (G6P) rather than products (F6P) as it approaches equilibrium.
What is the equilibrium ratio of [F6P] / [G6P] at 25°C (298 K)?
[F6P] / [G6P] is roughly ~0.5, corresponding to about 1 molecule of F6P to 2 molecules of G6P. The enzymatic conversion of G6P in F6P is not spontaneous in standard conditions. If we start from any equimolar concentration of G6P and F6P, we will get more G6P – meaning the reaction as depicted in Reaction (5.5) will go backwards. Yet, for glycolysis to proceed, the reaction must produce enough F6P to continue in the pathways. What if the cell metabolism requires to turn G6P into F6P, as is necessary for glycolysis?
The answer reveals why \(\Delta G\) is more important than \(\Delta G'^\circ\). If the ratio of [G6P] to [F6P] exceeds 2 – so if there is more G6P present relative to F6P in excess of the equilibrium ratio of 2:1 – then the number of conversions from G6P to F6P will be greater than the number of conversions from F6P to G6P. Let’s illustrate this with an example.
Which direction will Reaction (5.5) proceed, at 25 degrees Celsius, in a solution containing 43 mM G6P, 11 mM F6P, and 10 µM glucose-6-phosphate isomerase acting as a catalyst?
Using Equation (5.4), the \(\Delta G'^\circ\) value of the reaction, and the starting concentrations of F6P and G6P:
\(\Delta G\) =* \(\Delta G'^\circ + RT\)ln([F6P]/[G6P]) [F6P] = 11 mM; [G6P] = 43 mM
Δ*G = +*1.7 kJ/mol – 3.4 kJ/mol
ΔG = -1.7 kJ/mol
At this ~4:1 ratio of G6P to F6P, concentrations of F6P will increase. The reaction will go in the forward direction because G6P is in excess of its equilibrium ratio with F6P of 2:1.
NEED TO KNOW
Cells can manipulate the net direction of a reaction by maintaining the product/reactant ratio out of equilibrium.
Important to note. There is no place in the equation to insert the enzyme concentration (10 µM glucose-6-phosphate isomerase). Remember that enzymes to not change the equilibrium constant. Nor will they change the equilibrium ratio of reactants to products! Enzymes, like all catalysts, can only accelerate the interconversions between reactants and products. As you remember from Chapter 3, the enzyme concentration would determine the rate at which the reaction mixture reached equilibrium, but it could never change that equilibrium ratio.
This example illustrates how a reaction that is energetically unfavorable in standard conditions will nevertheless spontaneously generate product from reactants if there is a high enough concentration of reactants relative to products. The amount of reactants needed depends of course upon the equilibrium constant: lower equilibrium constants (and thus more unfavorable reactions) require a higher concentration of reactants to become favorable. It’s important to note that out-of-equilibrium reactions do not require a direct input of energy to occur – however, energy inputs may be required at other chemical reaction steps to maintain the out-of-equilibrium situation (see caveat below). Box 2 explains in more detail how the G6P to F6P conversion can work without energy.
BOX 2
In standard conditions, conversion of Glucose-6-phosphate in Fructose-6-phosphate by the enzyme glucose-6-phosphate isomerase is at equilibrium when F6P/G6P ~ 0,5.
Let’s imagine a cell with a compartment containing 200 molecules of G6P and 100 molecules of F6P. The reaction is at equilibrium, and no net F6P is produced. The cell starts to produce pyruvate via the glycolysis pathway, and consumes 80 molecules of F6P.
Does the equilibrium shift? And if so, how?
The cell now contains 200 molecules G6P and 20 molecules F6P. The new ratio [F6P]/[G6P] = 0.1
ΔG = ΔGʹ° + R*T*ln([F6P]/[G6P])
ΔG = -4.0 kJ/mol
The new equilibrium will be reached when [F6P]/[G6P] = 0,5. Considering no other reaction in the cells consume either G6P or F6P, the reaction will be at equilibrium when 53 molecules of F6P are produced, and the total number of 73 molecules of F6P is reached. This production is driven by equilibrium, and it does not need energy in the form of ATP.
The enzyme glucose-6-isomerase is not driving the reaction energetically: it is the free energy difference that results from the product/reactant concentration ratio to drive the reaction. The enzyme is merely facilitating and speeding the reaction up, like all catalysts do.
There is a very important caveat to this. While an out-of-equilibrium G6P to F6P reaction does not require energy to generate F6P product, the maintenance of lower concentrations of F6P to maintain the out-of-equilibrium product/reactant ratio often requires the direct input of chemical energy. So in the wider context, although the conversion of G6P to F6P can be driven forward without the direct input of energy when concentrations are out of equilibrium, maintaining the out-of-equilibrium conditions does require energy input (e.g. by continuously consuming F6P and decreasing its concentration). As we will see later, F6P is a reactant in the next step in glycolysis, which involves a phosphate transfer from ATP to F6P to create 1,6-fructose bisphosphate. This reaction is very thermodynamically favorable. Let’s see how so-called “ATP-driven reactions” are so favorable.
5.8. Enzymes and energy#
5.8.1. ATP Driven Bioenergetics#
We have seen in the previous section that the cell can take advantage of concentration gradients to manipulate the direction of chemical reactions. However, this is not always possible. It is often necessary to synthesize compounds against both unfavorable equilibrium constants and with high mass-action ratios that make the reaction even less favorable. How then is it possible to generate products of these reactions?
Fortunately, it is possible to couple unfavorable reactions with favorable reactions in a way that allows the otherwise-unfavorable reaction to become spontaneous. As you have learned from basic biology courses, cells maintain a pool of chemical energy carriers whose reactions are frequently used to drive reactions that would otherwise be unfavorable. One of these energy carriers is adenosine triphosphate (ATP). Cleaving the phosphates from ATP to generate either ADP and phosphate or AMP and pyrophosphate (PPi) is a strongly favorable reaction with a very high \(K_eq\) constant and a very negative \(\Delta G'^\circ\) value. Why is it thermodynamically allowed to use the free energy of ATP hydrolysis to drive unfavorable reactions? An important property helps us calculate the overall energetic costs of reactions coupled in metabolic pathways: free-energy changes of coupled reactions are additive.
NEED TO KNOW
The ΔG of sequential chemical reactions equals the sum of the ΔGs of the individual reactions.
For A \(\rightarrow\) B \(\rightarrow\) C, \(\Delta G\) of overall reaction is:
This principle is key to understand ATP-driven bioenergetics. How is this principle used in metabolism?
Let’s look at another unfavorable reaction: the first step in the glycolysis pathway, which is the conversion of glucose to glucose-6-phosphate:
Glucose + Pi 🡪 glucose-6-phosphate (G6P) + H2O \(\Delta G'^\circ\) = +13.8 kJ/mol
We could consider driving this forward with Le Chatelier’s principle by simply arranging for a high concentration of glucose and phosphate. However, considering the high positive \(\Delta G'^\circ\), this would require extremely high concentrations of glucose and phosphate that are not healthy for the cell. So what if we couple this reaction to ATP hydrolysis? ATP hydrolysis is very thermodynamically favorable:
ATP + H2O 🡪 ADP + Pi \(\Delta G'^\circ\) = -30.5 kJ/mol
Now let’s invoke the additivity of free energies. If we can somehow couple ATP hydrolysis with glucose phosphorylation, then the favorability of the ATP hydrolysis reaction far overcomes the unfavourability of glucose phosphorylation and the reaction becomes thermodynamically favorable. The simple arithmetic shows how the standard free Gibbs energy becomes negative:
Glucose + ATP + H2O 🡪 G6P + ADP + H2O
\(\Delta G'^\circ\) = (+13.8 kJ/mol) + (-30.5 kJ/mol) = -16.7 kJ/mol
So if we can harness the additivity of free energies in this abstract chemical equation, we will be able to phosphorylate glucose at the cost of one ATP. Again, this is analogous to overcoming the unfavourability of pushing a car to the top of a hill by combusting petrol in an engine that causes the wheels to turn. Fig. 5.1 depicts this phenomenon as a free energy diagram.
Enzymes leverage energy from a favorable reaction like ATP hydrolysis to drive an unfavorable reaction:
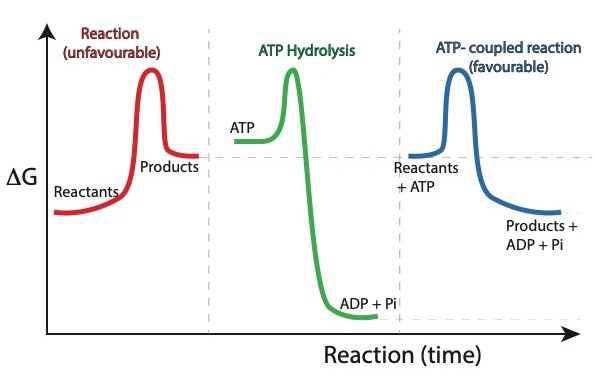
Fig. 5.1 Energy can be leveraged from a favourable reaction to drive an unfavourable one.#
But how enzymes use ATP “hydrolysis” to drive chemical reactions? How is the energy stored in the ATP phosphates channeled to catalyze thermodynamically-unfavorable reactions? The next section will explain how this works.
5.8.2. How enzymes couple unfavorable reactions with favorable reactions#
Let’s look at ATP hydrolysis again:
ATP + H2O 🡪 ADP + Pi \(\Delta G'^\circ\) = -30.5 kJ/mol
Removing one of the phosphates with water is the definition of hydrolysis. ATP is thermodynamically unstable relative to ADP and free phosphate: eliminating the terminal phosphate is strongly forward-driven. Why is this? One reason is that the three phosphate groups are negatively charged and are closely grouped together. As electrostatic charges of like sign repel, the three phosphates exhibit a powerful electrostatic repulsion that is relieved when one phosphate group is removed by transfer to another molecule. Electrostatic repulsion may contribute part of the thermodynamic favorability of phosphate transfer away from ATP; however, in real cells there are always abundant positively-charged counterions such as magnesium (Mg2+) that screen some of the negative charge between the phosphates. Another reason why ATP hydrolysis is favorable is the resonance stabilization (negative charge redistribution) across the phosphate ion that becomes possible when a phosphate is removed. This resonance stabilization is not possible when the phosphate is bound in ATP, which localizes the negative charges in a smaller volume – a situation that is less stable (Fig. 5.2).
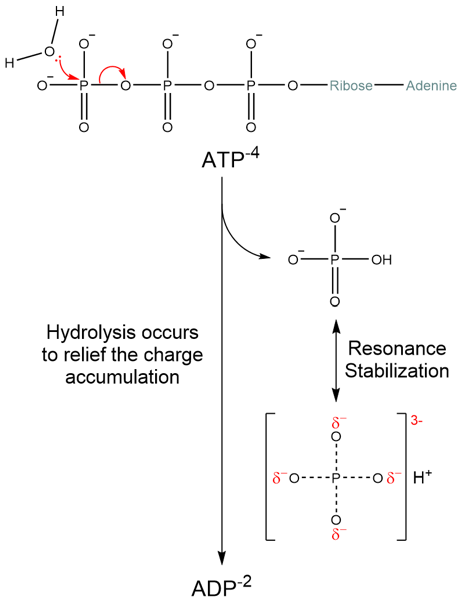
Fig. 5.2 ATP is thermodynamically more unstable than ADP. The electrostatic repulsion between phosphate groups is partially relieved in ADP.#
Whether for reasons of charge repulsion or resonance stabilization (likely both), the important outcome is that the transfer of a phosphate from ATP to an acceptor molecule is very likely to be thermodynamically favorable. What is meant by “acceptor molecule?” This is any molecule that accepts the phosphate from ATP. In the special case of ATP hydrolysis, water is the acceptor molecule. In the case of glucose phosphorylation, glucose is the acceptor molecule. In both cases, the transfer of phosphate from ATP to a new acceptor is thermodynamically favorable, since both reactions break apart the phosphates on ATP. This is the key to understanding how the energy represented in the phosphate bonds of ATP is transduced to drive unfavorable reactions forward (Fig. 5.3).
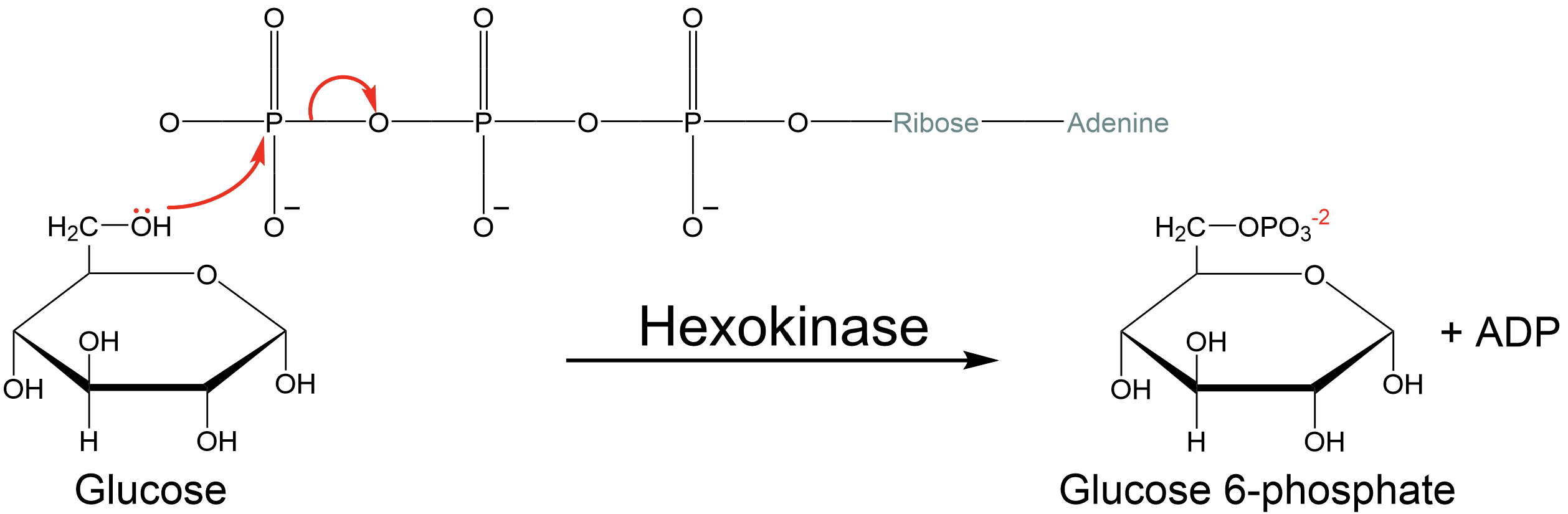
Fig. 5.3 Since the enzyme hexokinase catalyzes the transfer of the phosphate group from ATP to the hydroxyl group (-OH) of glucose as a phosphate acceptor to break ATP instead of using the hydroxyl of H2O as acceptor achieves many of the same results as hydrolysis (i.e. allowing resonance stabilization of the negative charge present on the phosphates), at the cost of destabilizing the glucose by converting it to glucose-6-phosphate.#
Let’s look at another example. Fig. 5.4 and Fig. 5.5 depict the synthesis of glutamine from glutamate, an ATP-driven reaction catalyzed by glutamine synthase. When depicted as in Fig. 5.4, it appears like ATP donated a phosphate directly to water, which somehow converted glutamate into glutamine. While Fig. 5.4 accurately represents the reactants and products at the start and finish of the overall reaction (ammonia (NH3) replaces the O- in the carboxylate group to generate an amide, while ATP is converted to ADP and free phosphate), the reaction actually happens in two steps that are depicted in Fig. 5.5: ATP transfers a phosphate to the O- in the carboxylate group, generating a chemically-unstable mixed anhydride (the C-O-P bond). Next, the ammonia forms a bond with the mixed anhydride carbon atom, breaking the anhydride complex and releasing phosphate. This better illustrates how glutamine synthase harnesses phosphate transfer from ATP to the carboxylate to drive the reaction forward.
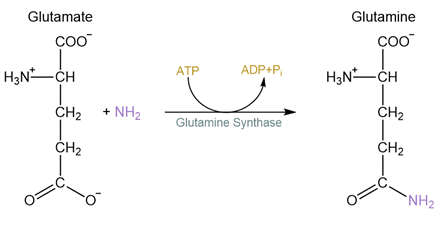
Fig. 5.4 ATP-driven glutamine synthesis depicted as a single step reaction.#
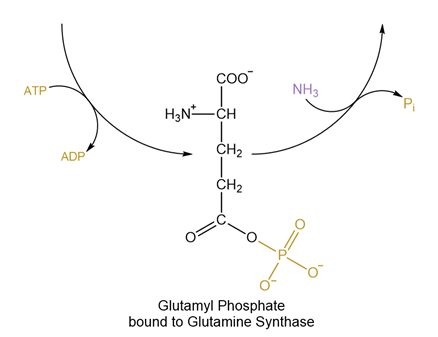
Fig. 5.5 ATP-driven glutamine synthesis depicted as a reaction constituted of 2 steps.#
5.8.3. ATP synthesis: what compounds have higher transfer energy than ATP?#
So ATP (and other so-called “high-energy compounds”) can be coupled with unfavorable reactions to generate products. But ATP production from ADP and phosphate is a very unfavorable reaction (\(\Delta G'^\circ\) = +30.5 kJ/mol). This means that the phosphate transferred to ADP to create ATP must come from a compound with an even higher energy of phosphate transfer. It turns out there are several compounds with sufficient transfer energy to create ATP from ADP. In the glycolysis pathway alone, there are two reactions that transfer phosphate to ADP. One reaction is the transfer of a phosphate from phosphoenolpyruvate (PEP) to ADP, which is catalyzed by pyruvate kinase.
What is the free energy of phosphate transfer from PEP to ADP? First, let’s look at the free energy of phosphate transfer from PEP to water (PEP hydrolysis):
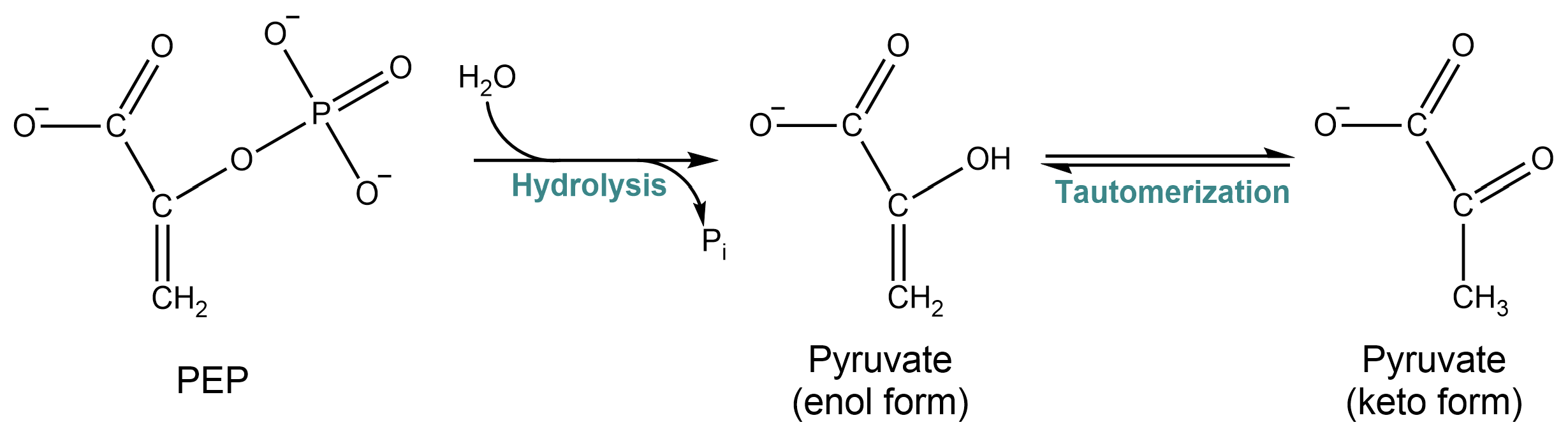
Fig. 5.6 ..#
Understanding why phosphate transfer from PEP is more energetically favorable than phosphate transfer from ATP requires a bit of organic chemistry background. The reversible tautomerization of pyruvate between enol and keto form heavily favours the keto form: enols are highly unstable. If you look at the tautomers, you’ll see that the interconversion moves a proton from a carbon atom to the oxygen atom. In PEP, the oxygen is bound to a phosphate. This “locks” the molecule in an unstable enol form. Transferring the phosphate away to any other molecule (such as ADP) allows the molecule to relax into its keto form. The difference in free energies between PEP and pyruvate and phosphate is -61.9 kJ/mol, considerably higher than the energy required to transfer a phosphate to ADP (Table 5.1):
Reaction |
\(\Delta G'^\circ\) [kJ/mol] |
|---|---|
PEP3- + H2O 🡪 Pyruvate- + HPO42- |
-61.9 |
ADP + Pi 🡪 ATP + H2O (Reverse ATP hydrolysis) |
+30.5 |
Pyruvate kinase catalyzes the group transfer of phosphate from phosphoenolpyruvate (PEP) to ADP. The reactions in Table 1 are therefore coupled. Since free energies of coupled reaction are additive:
Pyruvate and ATP production from PEP and ADP by pyruvate kinase is therefore a favorable reaction in standard conditions.
The transfer of phosphates from PEP to ATP, and from ATP to the many acceptor molecules, can be represented by a diagram representing the phosphate transfer potential of each compound (Fig. 5.7). Think of the compounds like steps in a waterfall and phosphates (like water) falling downward towards the bottom of the diagram. The diagram shows how phosphates can transfer from very high-energy compounds like PEP or 1,3-bisphosphoglycerate (which you will encounter in the glycolysis chapter) to ATP. ATP is the most abundant phosphate carrier with relatively high transfer potential and is used to distribute phosphates to acceptors such as glucose and glycerol. Ultimately, water is the final phosphate acceptor (yielding phosphate) with no favorable phosphate transfer potential.
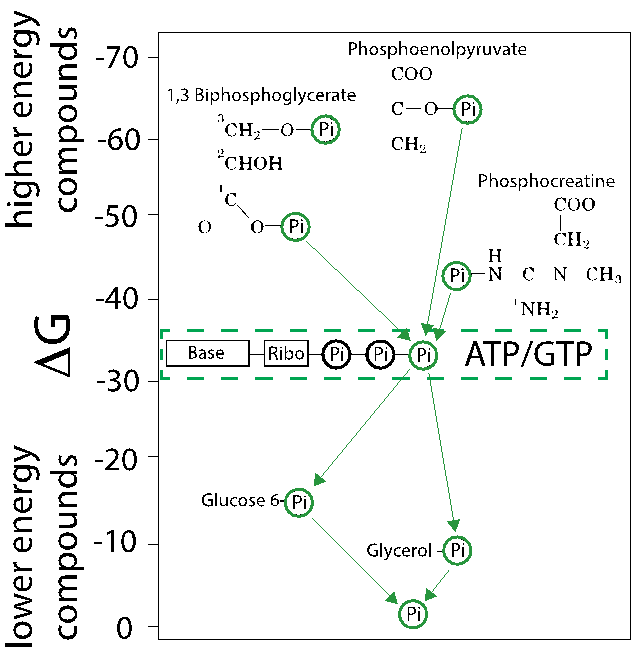
Fig. 5.7 A diagram showing the \(\Delta G'^\circ\) several compounds containing a phosphate group. The higher the energy, the more strongly favored hydrolysis is.#
5.8.4. ATP is one of several molecules with high transfer energies#
Phosphate transfers are one example of group transfer reactions involving the transfer of chemical groups from a donor to an acceptor. The transfer of acetyl groups is another example of group transfer. The metabolite acetyl-CoA is commonly used as an acetyl donor, just like ATP is a phosphate donor. The transfer of an acetyl group from acetyl-CoA generates coenzyme A (CoA):

Fig. 5.8 Structure of acetyl-CoA. The acetyl group is indicated in blue, the coenzyme A moiety is indicated in black.#
Just like phosphate transfer from ATP, the transfer of acetyl groups from acetyl-CoA to acceptor molecules is usually energetically favorable. Thioester bonds (bonds between a carbonyl carbon and a sulfur atom) are thermodynamically unstable relative to carbon-oxygen ester bonds so their hydrolysis has a negative \(\Delta G'^\circ\). This is illustrated by the hydrolysis of acetyl-CoA into acetate and CoA (equivalent to acetyl transfer to water):
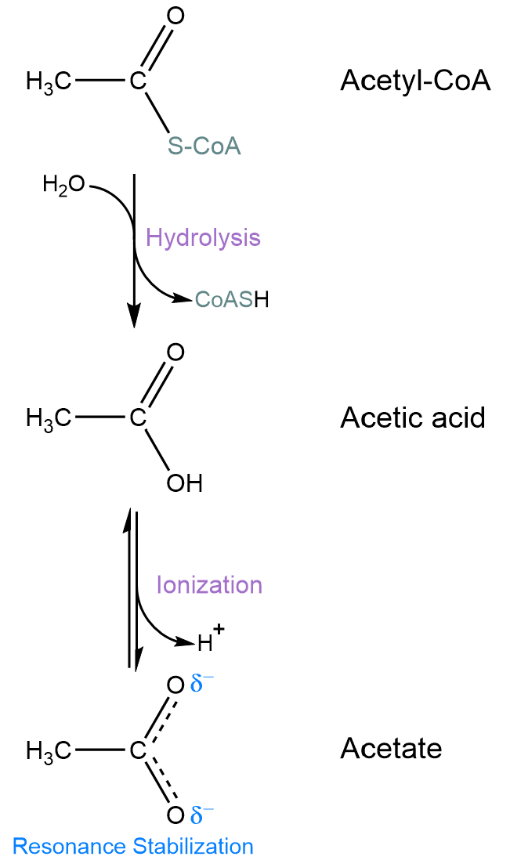
Reaction |
\(\Delta G'^\circ\) [kJ/mol]* |
|---|---|
Acetyl-CoA + H2O 🡪 Acetate- + CoA + H+ |
- 31.4 |
Transfer of the acetyl group of acetyl-CoA to oxaloacetate generates citrate as product, entering the TCA cycle:
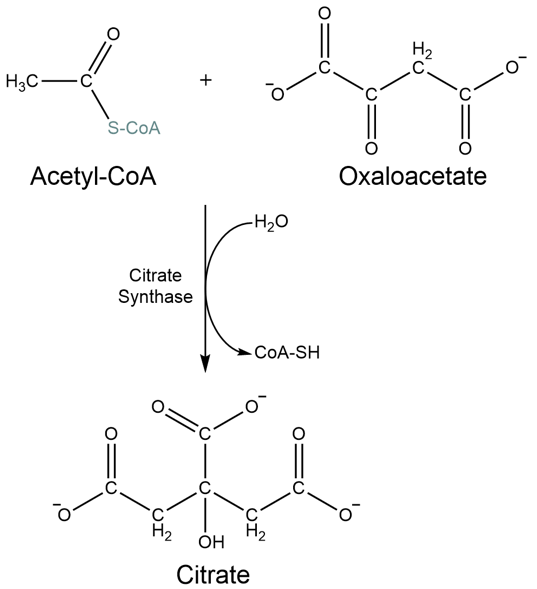
Fig. 5.9 The first step of the TCA cycle produces citrate from acetyl-CoA and oxaloacetate, a very favourable reaction#
Reaction |
\(\Delta G'^\circ\) [kJ/mol]* |
|---|---|
Acetyl-CoA + H2O 🡪 Acetate- + CoA + H+ |
- 31.4 |
Acetyl-CoA + oxaloacetate 🡪 citrate |
-31.2 |
5.8.5. On the instability of ATP as an energy carrier#
ATP is a useful compound for generating products of reactions that would otherwise be thermodynamically unfavorable because ATP is thermodynamically unstable. This term means that at equilibrium, the hydrolysis products of ATP (ADP and phosphate) will have far higher concentrations than ATP. However, it sounds odd that cellular metabolism transmits chemical energy via an “unstable” compound. If ATP is unstable, doesn’t it spontaneously fall apart independently of catalyzed reactions?
The resolution to this question is to distinguish between thermodynamic instability and kinetic instability. These are important concepts in biochemistry. Thermodynamic instability is simply stating that the equilibrium between a compound and the products of a reaction involving the compound as a reactant heavily favors the reaction products – at equilibrium, there will be very little of the reactant compound remaining. However, comparing the stabilities of reactants and products says nothing about the rate of the reaction that will generate the products. To describe compounds that rapidly convert into products in the absence of a catalyst, we use the term kinetic instability. A kinetically-unstable molecule is a molecule that will decay into product relatively quickly – i.e., the reactant will not persist.
The differences between thermodynamic instability and kinetic instability is illustrated in Fig. 5.10:
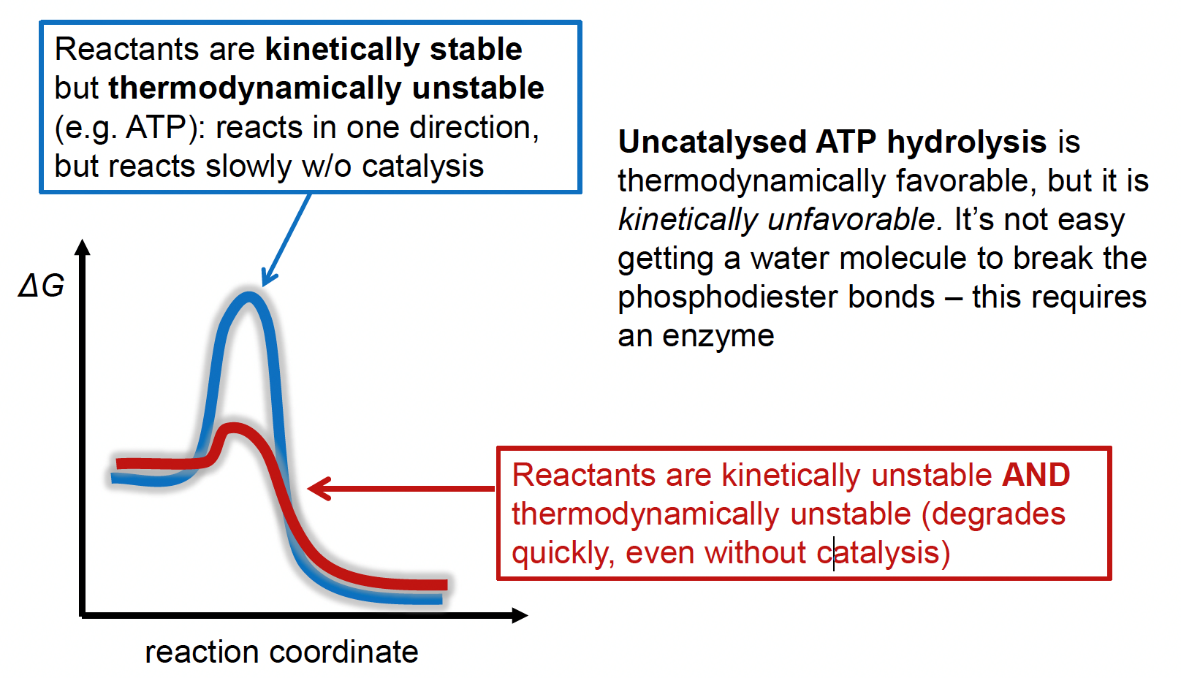
Fig. 5.10 A schematic reaction showing the differences between thermodynamic and kinetic instability. Both reactions (red and blue) are thermodynamically unstable, as seen by the lower energy state of the products versus the reactants. This means the equilibrium for both reactions will (heavily) favor the reactants. However, the blue reaction is unlikely to proceed spontaneously due to the high energy barrier, this makes the blue reaction kinetically stable.#
So ATP is thermodynamically unstable (allowing its coupling with unfavorable reactions) but it is kinetically stable because spontaneous ATP hydrolysis into ADP and water is very slow in the absence of a catalyst (such as an enzyme). This means that the cell can happily make ATP without worrying much about losing ATP in random hydrolysis reactions.
A similar compound that is thermodynamically unstable but kinetically stable is paper. In Earth’s atmosphere (20% oxygen), the paper in your notebook is thermodynamically unstable relative to its combustion products (carbon dioxide and water). However, because paper is kinetically stable, you do not need to worry that it will spontaneously catch fire in your hands. On a very long timescale, white paper will begin to turn yellow as it slowly reacts with atmospheric oxygen (as you can see with the pages of old books). Fortunately this spontaneous oxidation of paper is too slow at room temperature to generate sufficient heat to start a fire.
5.9. Induced fit theory: the structural basis of ATP-driven bioenergetics#
Let’s consider the phosphate transfer reaction from ATP to glucose from a thermodynamic perspective to understand how statistically unlikely it is. As described in the previous section, ATP is kinetically stable but thermodynamically unstable. An enzyme that catalyzes phosphate transfer from ATP is effectively eliminating the kinetic stability of a bound ATP molecule and increasing the probability that ATP will lose a phosphate to some acceptor molecule. What molecule in an aqueous solution is most likely to accept the phosphate from a destabilized ATP? Let’s say we have a 0.1 mM solution of glucose in water. In this situation, we actually have two potential phosphate acceptors: glucose (the intended target of the enzyme hexokinase, which transfers phosphate from ATP to glucose) and water. Which is more likely to accept the phosphate?
In most aqueous conditions (such as the interior of a cell) the concentration of water in molar terms is ~55 M. Our example solution has 0.1 mM glucose. This means that water is 550,000 times more concentrated than glucose! In this situation, where an enzyme is catalyzing phosphate transfer from ATP, water will be the most likely acceptor molecule. Since we’re trying to phosphorylate glucose, an enzyme that simply catalyzes phosphate transfer from ATP without being selective in which acceptor molecule receives the phosphate we will lose a lot of phosphates to water before phosphorylating any glucose. So how do enzymes prevent nonspecific phosphate transfer to water, especially given that water is so much more concentrated than any alternative acceptor molecule?
What prevents hexokinase from hydrolyzing ATP releasing phosphate (Fig. 5.11), instead of transferring the phosphate to glucose (Fig. 5.12)?
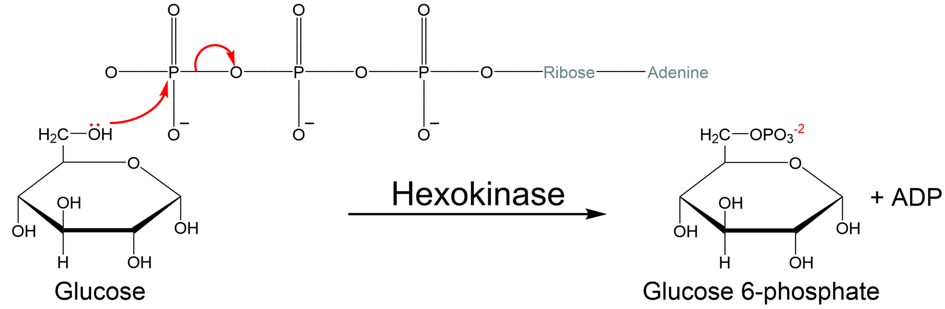
Fig. 5.11 ATP hydrolysis with phosphate release.#

Fig. 5.12 ATP hydrolysis with phosphate transfer to glucose.#
To answer this question, it is useful to think of the catalytic mechanism enacted by the active site of the hexokinase. Hexokinase (like all enzymes that catalyze phosphate transfer) stabilizes the transition state of the phosphate transfer reaction. This involves stabilizing the cleavage of the phosphate-oxygen bonds within ATP. If a poorly-designed nonselective hexokinase formed the catalytic interactions with ATP that destabilize the bonds between the phosphate groups, any acceptor molecule that also happens to be in the active site with ATP is likely to take the phosphate (Fig. 5.13). As water is so much more abundant than glucose, ATP hydrolysis would be much more likely than glucose phosphorylation. How does hexokinase prevent hydrolysis?
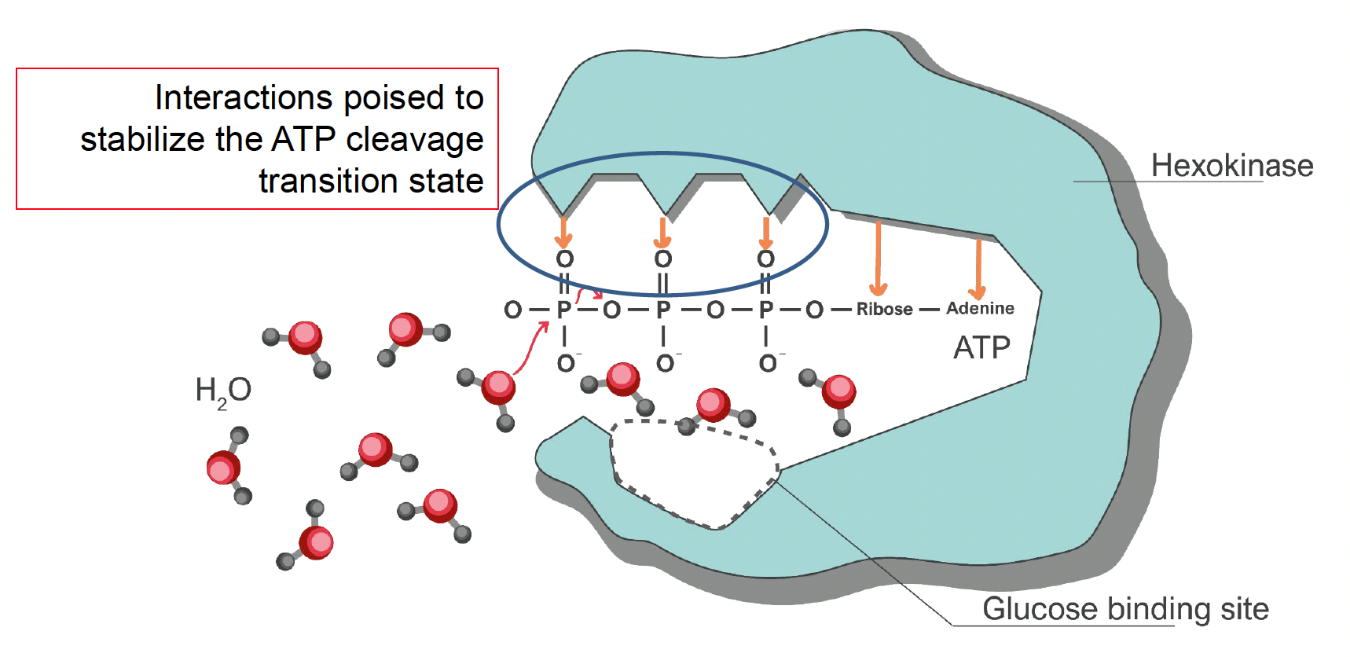
Fig. 5.13 Hypothetical active site depiction of a nonselective hexokinase. Interactions between enzyme and the ATP phosphates formed in the absence of glucose that stabilize phosphate transfer would allow nonselective transfer of phosphates to water.#
This question was asked presciently by Daniel Koshland, an eminent biochemist from the time before protein structures were routinely obtained. Enough was known about enzyme active sites and their selectivity for substrate molecules that the prevailing metaphor for enzyme-substrate interactions, proposed by Emil Fischer in 1890, was a lock and key mechanism: the “lock” (analogous to the enzyme active site) was structurally complementary to the “key” (analogous to a substrate molecule). The unstated consequence of this metaphor is that enzyme structures are rigid and stable, much like a lock does not change its shape when a key is inserted. If this were true, and hexokinase were to passively allow ATP, water, and glucose to diffuse in and out of its rigid and unmoving active site, the simple fact of the high concentration of water would suggest that ATP hydrolysis would be the most likely reaction to happen. Thus, Koshland speculated, the enzyme must be doing something special to prevent ATP hydrolysis.
As it turns out, Daniel Koshland was correct. The hexokinase active site prevents hydrolysis because it does not form the interactions that stabilize phosphate transfer until after glucose has also bound in the active site. When only ATP has bound without glucose, the enzyme does not interact with the phosphates (Fig. 5.14).
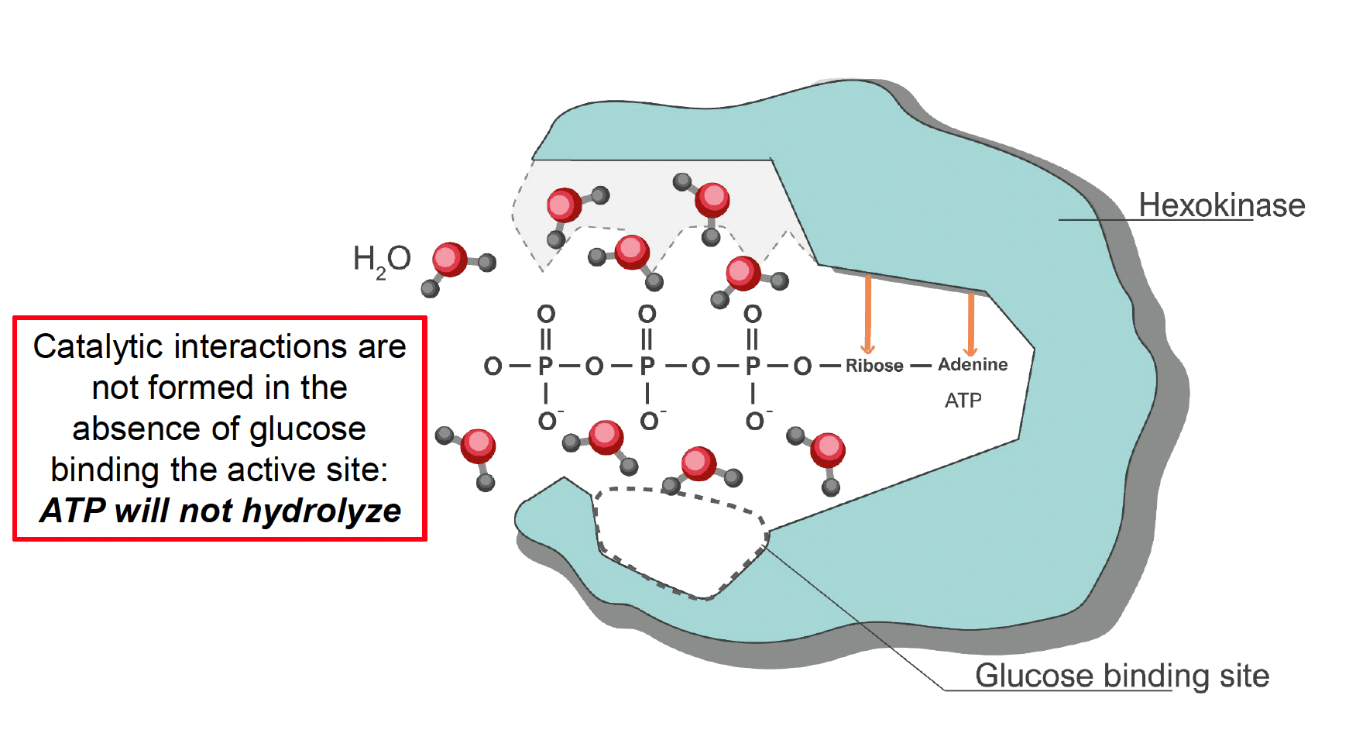
Fig. 5.14 Hexokinase active site conformation when glucose is not bound#
Glucose binding induces a dramatic structural change that pushes all water molecules out of the active site to ensure that ATP reacts only with glucose (Fig. 5.15):
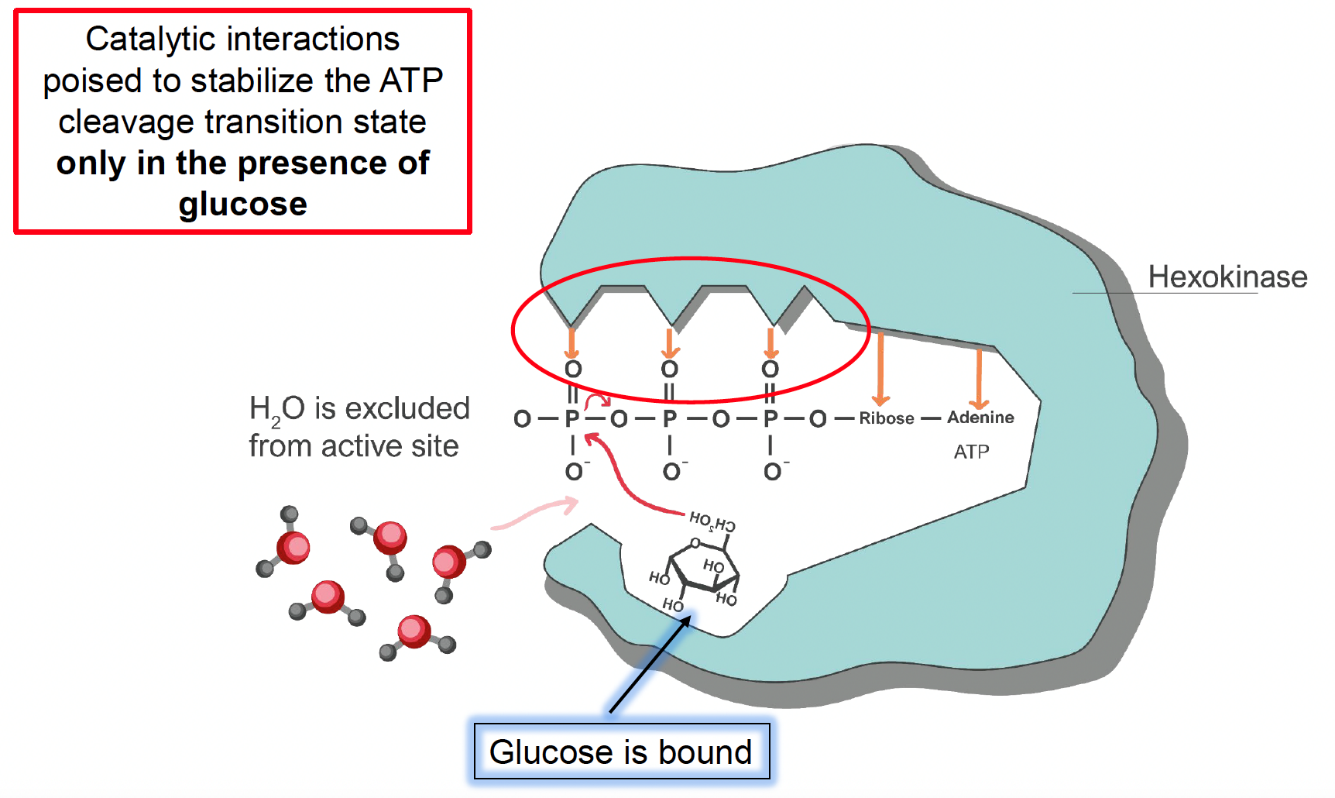
Fig. 5.15 Hexokinase active site conformation when glucose is bound.#
This model conflicts with the “lock and key” theory of enzyme-substrate interactions. Instead of the enzyme playing a relatively passive role by simply positioning active site residues in a fixed manner (much like insertion of a key does not change the structure of a lock), glucose binding to hexokinase induces the hexokinase to change its structure in a way that completely excludes water from the active site. This is called the “induced fit” mechanism because glucose binding induces the enzyme to better fit to its substrates ATP and glucose. This mechanism introduced the notion into biochemistry that enzymes are often structurally dynamic, not static and rigid structures as previously thought.
Hexokinase structures (available on the Protein Data Bank) illustrate the conformational changes triggered by the binding of glucose:
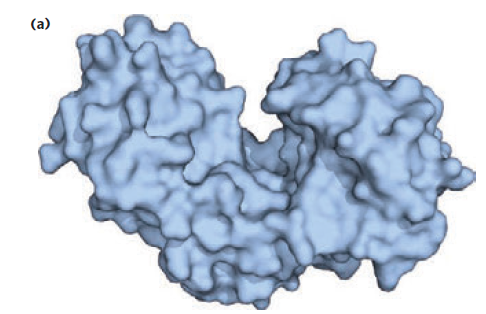
The active site is in the cleft. That’s where the substrates bind. Upon substrate binding, the enzyme changes its shape:
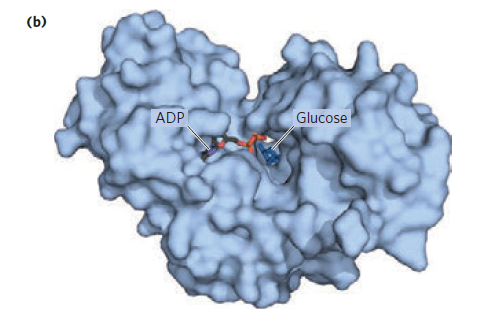
Glucose binding induces a dramatic structural change of the overall enzyme, with the enzyme acquiring a closed state that promotes substrate positioning to favor Pi<\sub> transfer. The enzyme active site wraps tightly around glucose and the ATP phosphates, excluding water and ensuring that the phosphate lands on the hydroxyl group of glucose:
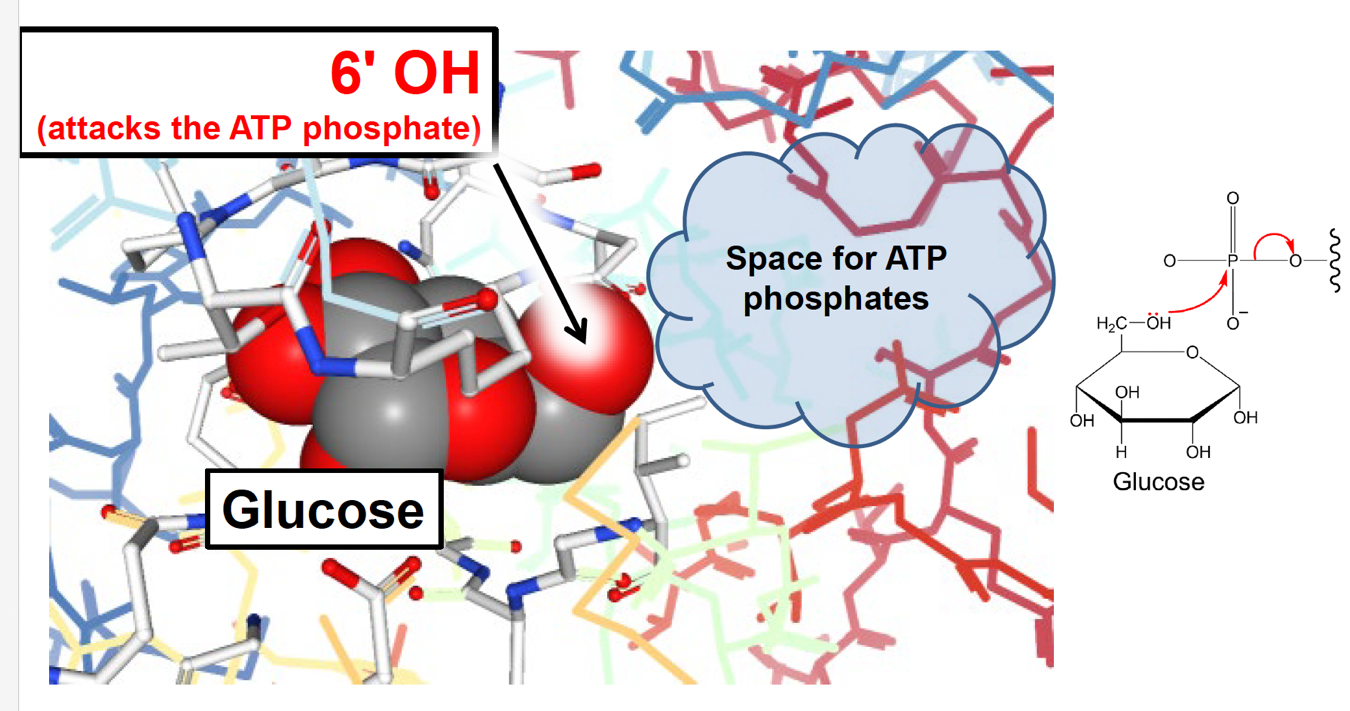
A very nice test of this theory was performed in reactions that substitute the usual target glucose with the wood sugar xylose. Xylose is structurally similar to glucose except the 6ʹ hydroxyl group that accepts the phosphate (Fig. 5.19):
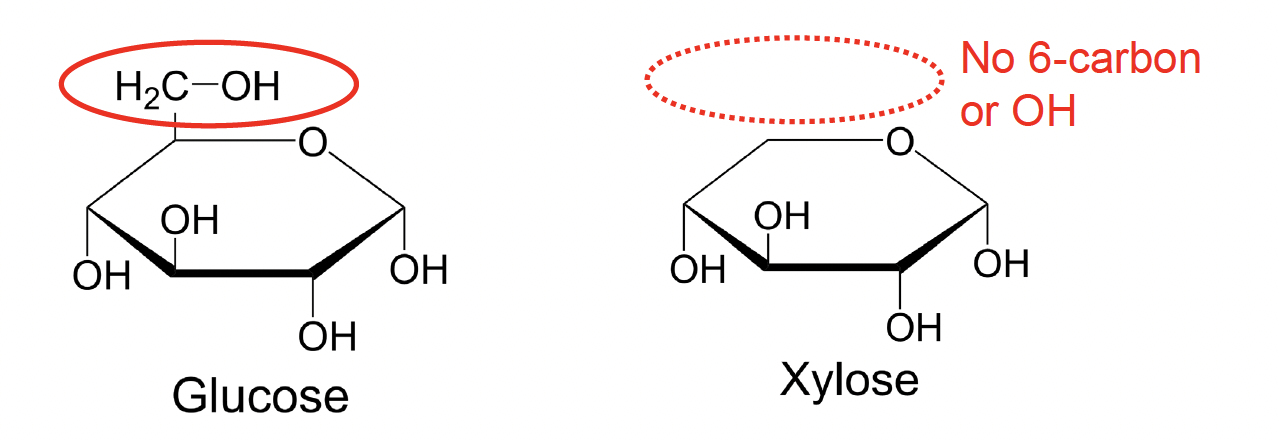
Fig. 5.19 Xylose does not include a hydroxyl acceptor group in the corresponding position compared to glucose.#
Binding xylose in the hexokinase active site leaves a small space that would ordinarily be occupied by the 6ʹ hydroxyl group (Fig. 5.20). As it turns out, xylose triggers the same structural change in hexokinase that glucose does (likely due to its similar structure), but due to the small cavity remaining in the active site, water is not entirely excluded. As a result, hexokinase is a very efficient ATP hydrolase when mixed with xylose.
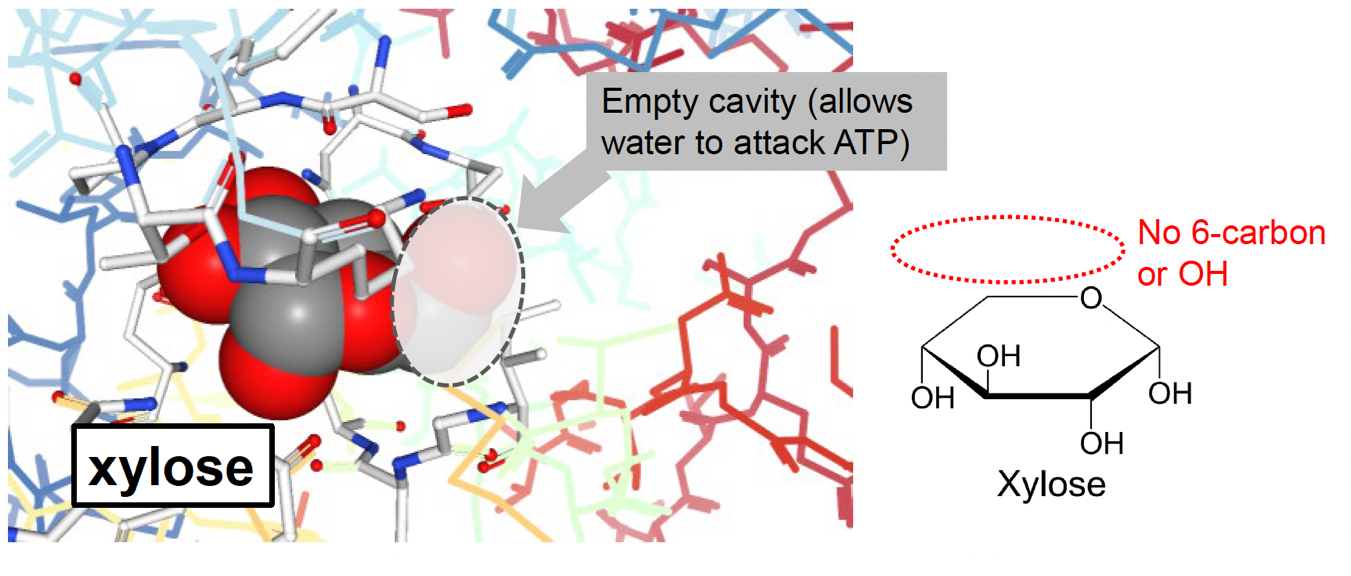
Fig. 5.20 In environments where xylose is more abundant than glucose, the active site of hexokinase can form enough interactions with xylose as a substrate analog, but will not be able to accept a phosphate from ATP, promoting ATP hydrolysis and phosphate transfer to a molecule of water. PDB structure 1V4S [2].#
The induced fit strategy is used by many enzymes that catalyze group transfer reactions. Induced fit ensures that strongly forward-driven reactions are performed with the correct substrates by excluding more abundant substrates (especially water).
Camillo Rosano, Elisabetta Sabini, Menico Rizzi, Daniela Deriu, Garib Murshudov, Marzia Bianchi, Giordano Serafini, Mauro Magnani, and Martino Bolognesi. Binding of non-catalytic atp to human hexokinase i highlights the structural components for enzyme-membrane association control. Structure, 7(11):1427–1437, 1999. doi:10.1016/S0969-2126(00)80032-5.
Kenji Kamata, Morihiro Mitsuya, Teruyuki Nishimura, Jun-ichi Eiki, and Yasufumi Nagata. Structural basis for allosteric regulation of the monomeric allosteric enzyme human glucokinase. Structure, 12(3):429–438, 2004. doi:10.1016/j.str.2004.02.005.