9. Wisselstroomschakelingen

In dit hoofdstuk bestuderen we elektronische schakelingen met een wisselstroombron. Condensatoren en spoelen werken geheel tegengesteld op wisselstromen wat het mogelijk maakt om effectief audio weer te geven.

9.1. Wisselstroom

Een typische manier om een wisselstroom te genereren is met een dynamo. Dit is geheel kwantitatief uit te rekenen met behulp van de wet van Faraday.

9.1.1. Numeriek voorbeeld van het numeriek berekenen met de wet van Faraday hoe een dynamo werkt

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Image

Een dynamo is een elektromotor, die met een aandrijving energie induceert. Je kent het misschien wel van een fiets, waar je band een dynamo aandrijft, die spanning induceert om je fietslampje te laten branden. De mate waarin een dynamo spanning induceert volgt uit de wet van Faraday:

\[ \epsilon = -\frac{d\Phi_{B}}{dt} \]

De EMF, ElectoMagnetic Force (\(\epsilon\)), is afhankelijk van de verandering van magnetische flux (\(\Phi_{B}\)) in de tijd, en geeft energie per lading aan.

Om een stroom te induceren moet een dynamo er dus voor zorgen dat er een continue verandering is in het magnetisch veld. Meestal gebeurt dit door een spoel te laten draaien in een magnetisch veld, waardoor de magnetische flux door de spoel verandert in de tijd.

In ons voorbeeld hebben wij twee permanente magneten, een Noordpool en een Zuidpool. Tussen deze twee mageneten hebben we een spoel, verbonden aan een fietslampje. We gaan kijken hoeveel energie we leveren door de spoel rond te draaien. Hieronder zie je een heel versimpelde afbeelding van deze setup. De spoel is aan de onderkant verbonden met een verder circuit, bijvoorbeeld een lampje voor je fiets.|

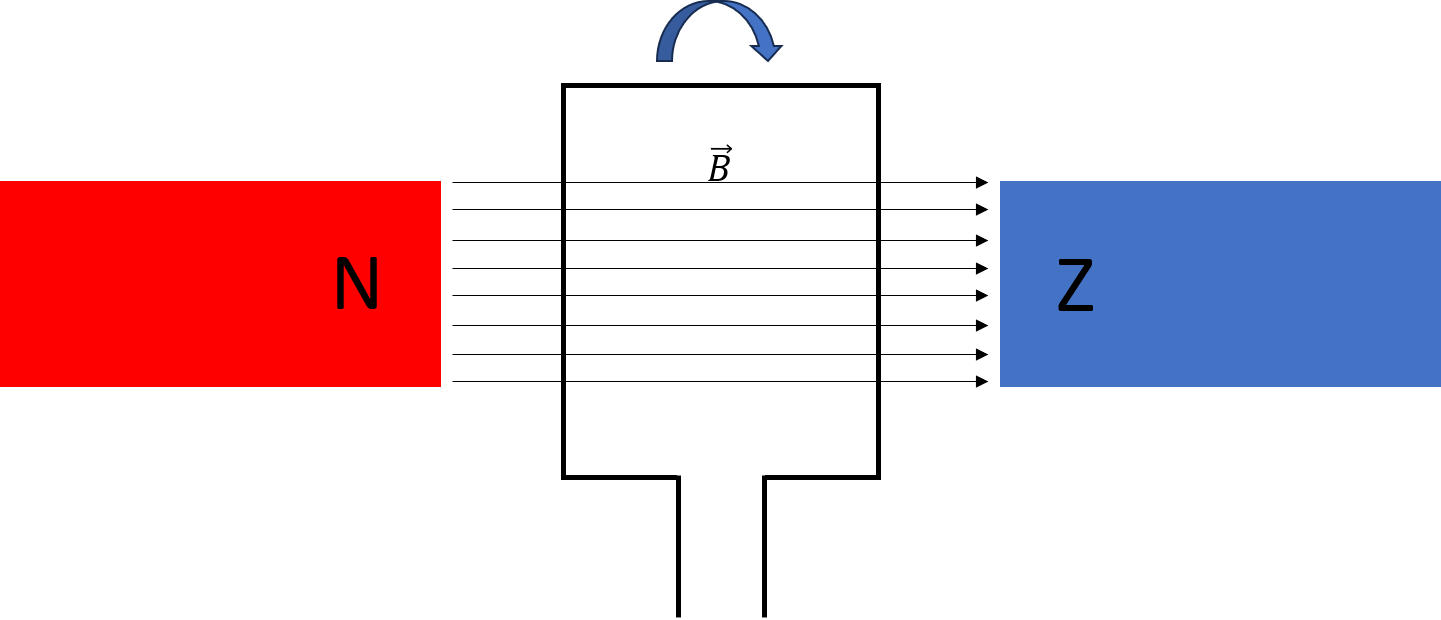
De magnetische flux is gelijk aan het inproduct van het magneetveld met het oppervlakte.

\[ \Phi_{B} = \vec{B}\cdot\vec{A} = BA cos(\theta) \]

Als we de spoel draaien met een constante hoeksnelheid \(\omega = 2\pi f\), veranderd de hoek theta: \(\theta = 2\pi ft\). Wanneer de spoel draait veranderd dus get oppervlakte waardoor het magnetisch veld loopt, en daarmee veranderd dus de flux. Dit betekent dat de flux op tijdstip \(t\) gelijk is aan:

\[ \Phi_{B}(t) = BA cos(2\pi ft) \]

Oftewel, we kunnen de EMF berekenen!

\[ \epsilon = -\frac{d\Phi_{B}}{dt} = BA2\pi fsin(2\pi ft) \]

We kunnen hieruit zien, dat wanneer we de EMF willen verhogen, we een drietal dingen kunnen doen: 1. Het magneetveld verhogen, 2. Het oppervlakte kunnen verhogen, of 3. De frequentie verhogen. In de praktijk wordt het oppervlakte sterk verhoogd door gebruik te maken van meerdere wikkelingen in een spoel, zodat het magneetveld door 100 of 1000 spoelen gaat, in plaats van 1, waardoor ook de EMF sterk wordt verhoogd.

We gaan nu een dynamo doorrekenen. We nemen wat standaard waarden voor een magneet, en een oppervlakte van een spoel. We geven een grote draai aan de spoel, en we gaan kijken wat voor en EMF we krijgen!

Bval = 5 #Tesla
Aval = 2 #m2
f = 5 #Hz
N = 100
t = np.linspace(0,0.5,N)

Bvec = Bval*np.array([1,0])
# Direction of our B-field, in 2D

Avec = Aval*np.ones((N,2))
Avec[:,0] = Avec[:,0]*np.cos(2*np.pi*f*t)
Avec[:,1] = Avec[:,1]*np.sin(2*np.pi*f*t)
# Here we have the changing area vector.

Flux = np.dot(Avec[:],Bvec)

We hebben nu de flux op elk tijdstip, en moeten nu alleen nog een afgeleide berekenen. We doen dit door middel van de central difference method.

plt.figure(figsize=(15,5))
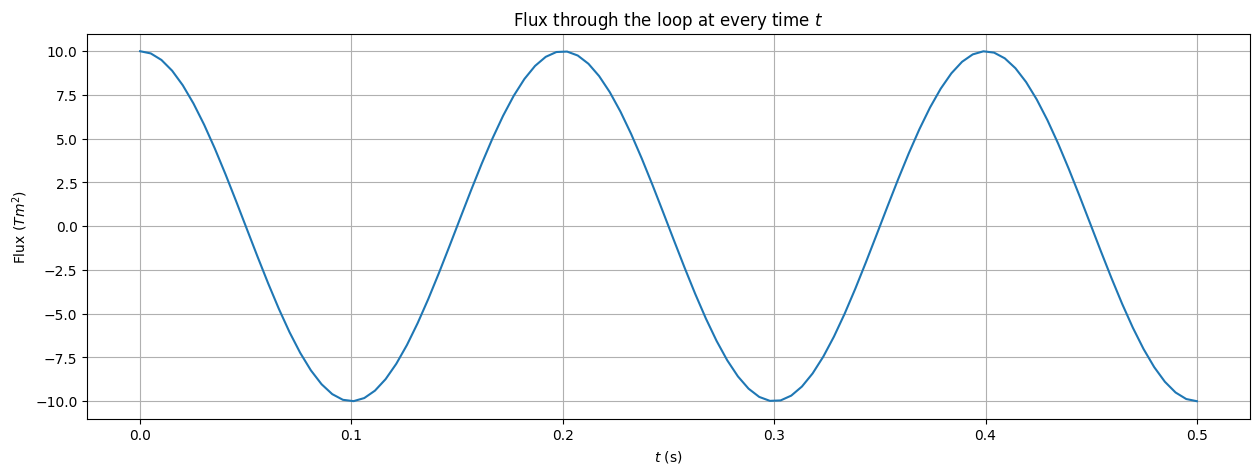
plt.plot(t,Flux)
plt.xlabel('$t$ (s)')
plt.ylabel('Flux ($Tm^{2}$)')
plt.title('Flux through the loop at every time $t$')
plt.grid()
plt.show()

dt = t[1] - t[0]

EMF = np.zeros(N-2)

for i in range(1,N-1):
    EMF[i-1] = -(Flux[i+1] - Flux[i-1])/(2*dt)

# Note that the central difference method requires our resulting array to be slightly smaller, 
# as to be able to calculate the differences. As such, we also need to change our time array in the plot.

plt.figure(figsize=(15,5))
plt.plot(t[1:-1],EMF)
plt.xlabel('$t$ (s)')
plt.ylabel('EMF (J)')
plt.title('EMF at time $t$')
plt.grid()
plt.show()

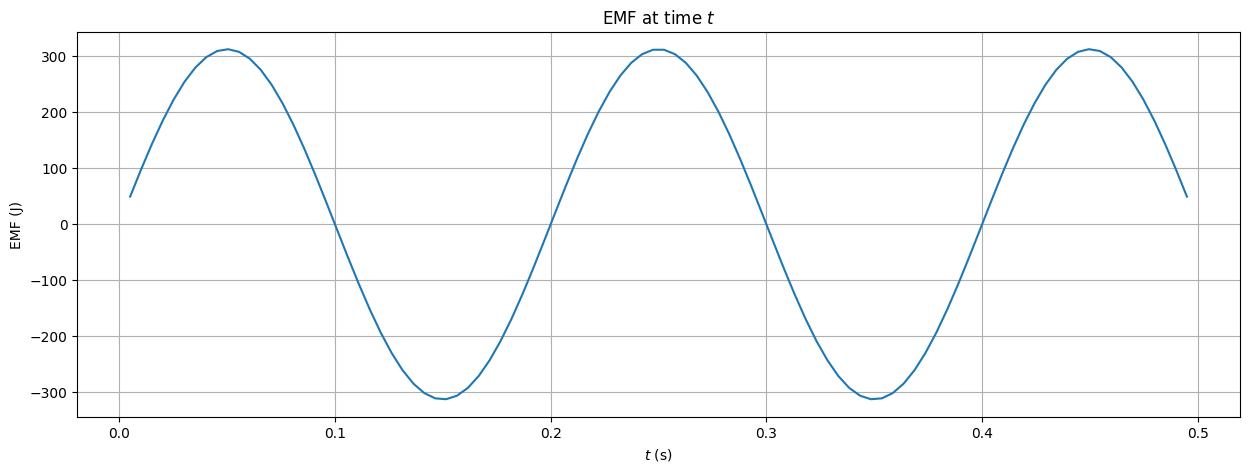
We kunnen dit vergelijken met een theoretische doorrekening van de Flux verandering. Uit de gegevens hierboven kunnen we een theoretische flux berekenen.

Flux_theory = Bval*Aval*np.cos(2*np.pi*f*t)
EMF_theory = Bval*Aval*2*np.pi*f*np.sin(2*np.pi*f*t)

plt.figure(figsize=(15,5))
plt.plot(t[1:-1],EMF)
plt.plot(t,EMF_theory, ls='dashed',color='black')
plt.xlabel('$t$ (s)')
plt.ylabel('EMF (J)')
plt.title('EMF at time $t$')
plt.grid()
plt.show()

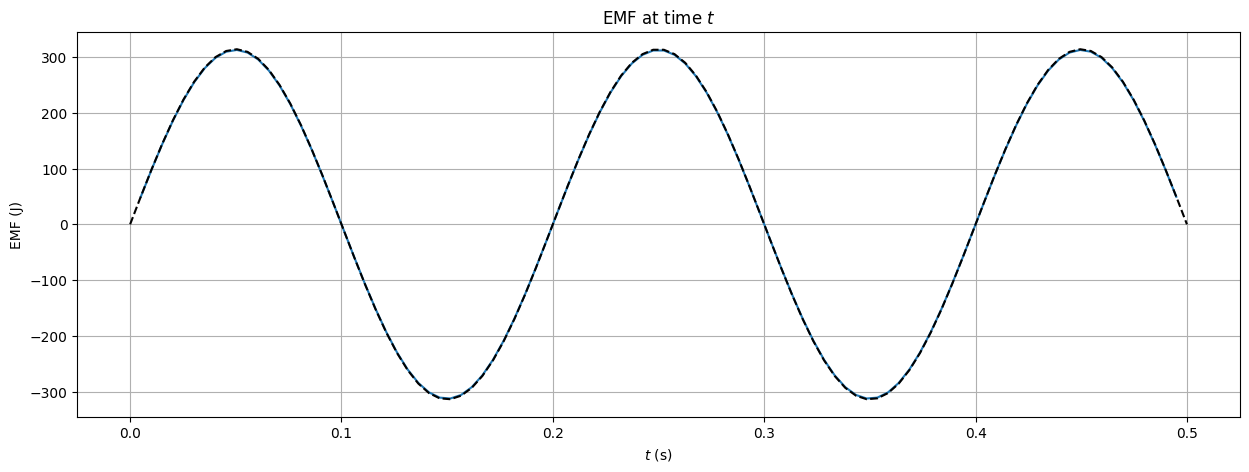
Onze doorrekening is precies wat we verwachten vanuit de theorie!

Voor berekeningen is het noodzakelijk om de eigenschappen van een wisselstroom volledig te beschrijven.

9.2. Condensatoren, spoelen en weerstanden in een wisselstroomschakeling

In deze video worden fasor-diagrammen uitgelegd. Deze fasoren zijn cruciaal om wisselstroomschakelingen goed te begrijpen. Deze fasoren worden gebruikt om de spanning over een wisselstroomschakeling met een weerstand en een condensator volledig te beschrijven.

Bij de analyse van een wisselstroomschakeling met een spoel komt het begrip inductieve reactantie naar voren. Dit is nodig om complexere schakelingen te analyseren.

In deze video bestuderen we het tegengestelde gedrag van condensatoren en spoelen in de limieten van lage en hoge frequentie wisselspanningsbronnen. Hiermee is het mogelijk om snel schakelingen te analyseren.

9.3. Oscillerende schakelingen

Met een simpele schakeling met alleen maar een condensator en een spoel (zogenaamd LC-schakeling) is het mogelijk om oscillaties te krijgen die wiskundig geheel aanloog aan een massa-veer-systeem te zijn beschrijven.

Door aan bovenstaand voorbeeld een weerstand toe te voegen (zogenaamd RLC-schakeling) treedt er demping op, geheel analoog aan de gedempte oscillator.

9.4. Aangedreven RLC-schakelingen

Veel audio-systemen zijn te beschrijven als aangedreven RLC-schakelingen. In deze video analyseren we kwalitatief deze schakeling. De uitkomst is dat er een resonantie gaat optreden wanneer de reactanties van condensator en spoel gelijk zijn.

In deze video geven we de volledige kwantitatieve analyse van het systeem.

Het vermogen gedisipieerd in de verschillende elementen van de schakeling hangt sterk af van de frequentie. Dat wordt in deze video uitgerekend.

9.5. Voorbeeldberekeningen aan RLC-schakelingen

Dit is een voorbeeld van een vroegere tentamensom.

In deze video wordt uitgerekend hoe met behulp van het instellen van weerstanden, condensatoren en spoelen de spanning van een versterker optimaal naar de juiste luidspreker wordt door gestuurd.

Hoe kan je de capaciteit van een condensator meten? In deze video leggen we uit hoe je dat kan doen via een meting van de reactantie.

9.6. Numerieke berekening van het effect van resonantie op een gedreven RLC-schakeling

We gaan hier onderzoeken wat de invloed is van verschillende frequenties op de voltages van de componenten in een gedreven RLC circuit.

Een gedreven RLC cicuit bestaat uit een AC spanningsbron die, met een bepaalde frequentie een voltage leverd aan een circuit, bestaande uit een weerstand (R), een Spoel (L), en een condensator (C). Een spoel en een condensator reageren beiden verschillend op veranderingen in stroom en voltages. De condensator levert kortsluiting bij een te snel spanningsverschil, waar een spoel een kortsluiting geeft bij een te snel stroomverschil.

Dit hangt allemaal samen met het idee van impedantie; een mate van de weerstand van een component in het systeem. Wij verstaan drie impedanties: \(X_{C}\), de impedantie van de condensator, \(X_{L}\), de impedantie van de spoel, en \(Z\), de impedantie van het totale circuit.

\[\begin{split} X_{C} = \frac{1}{\omega\times C} \\ \end{split}\]

\[\begin{split} X_{L} = \omega\times L \\ \end{split}\]

\[ Z = \sqrt{R^{2} + (X_{L} - X_{C})^{2}} \]

Met deze drie concepten kunnen we gaan kijken naar het voltage in de verschillende componenten, onder verschillende spanning.

Zoals we weten is het voltage van een eenvoudig circuit (een batterij en een weerstand), gelijk aan \(V = I\times R\). Precies dit gebruiken we ook voor de verschillende componenten in een RLC circuit:

\[\begin{split} V_{C} = I_{C}\times X_{C} \\ \end{split}\]

\[ V_{L} = I_{L}\times X_{L} \]

We hoeven dus alleen te kijken naar de stroom door de componenten! Die berekenen we met behulp van de piek voltage, en de frequentie van de stroombron:

\[\begin{split} I_{C} = \frac{V_{peak}}{Z} sin(\omega\times t - \frac{\pi}{2}) \\ \end{split}\]

\[ I_{L} = \frac{V_{peak}}{Z} sin(\omega\times t + \frac{\pi}{2}) \]

Wat hier belangrijk is om op te merken, is het feit dat de stroom in een condensator achterloopt op de gegenereerde stroom, en de stroom door een spoel voorloopt op de gegenereerde stroom.

Nu we al deze concepten in handen hebben, kunnen we gaan kijken wat er gebeurd met het systeem als we de frequentie veranderen.

import numpy as np
import matplotlib.pyplot as plt

V_p = 5 # V
N = 1000
t = np.linspace(0,0.01,N)

L = 1e-2 #Henry
C = 1e-5 #Fahrad
R = 10 #Ohm

We definiëren eerst het piek voltage, de tijdsstappen die we gaan berekenen, en de waardes van de weerstand, spoel, en condensator.

def Voltages(omega,R,L,C,t):
    
    X_C = 1/(omega*C)
    X_L = omega*L
    
    Z = np.sqrt(R**2 + (X_L + X_C)**2)
    
    I_C = V_p*np.sin(omega*t - np.pi/2)/Z
    I_L = V_p*np.sin(omega*t + np.pi/2)/Z

    V_C = X_C*I_C
    V_L = X_L*I_L
    V = V_C + V_L
    
    return V, V_C, V_L

We berekenen de voltages aan de hand van de hierboven gegeven vergelijkingen. We zien dat het uiteindelijke voltage door het circuit wordt gegeven door de optelling van het voltage door de condensator, en de spoel. Ook zien we, dat wanneer de batterij de resonantie frequentie geeft, het totale voltage 0 is. De resonantie frequentie wordt gegeven, wanneer \(X_{C} = X_{L}\). Dit gebeurt bij:

\[ \omega_{0} = \frac{1}{\sqrt{LC}} \]

omega_0 = 1/(np.sqrt(L*C))

# frequencies = np.linspace(0.5*omega_0,1.5*omega_0,3)
frequencies = [omega_0/1.5, omega_0,1.5*omega_0]
labs=["2/3 resonance freq", "resonance freq ", "3/2 resonance freq"]

V = np.zeros((len(frequencies),N))
VC = np.zeros((len(frequencies),N))
VL = np.zeros((len(frequencies),N))

for i in range(len(frequencies)):
    V[i] = Voltages(frequencies[i],R,L,C,t)[0]
    VC[i] = Voltages(frequencies[i],R,L,C,t)[1]
    VL[i] = Voltages(frequencies[i],R,L,C,t)[2]

print('Resonance frequency =',round(omega_0),'Hz')
plt.figure
for i in range(len(frequencies)):
    plt.title(labs[i])
    plt.xlabel('t(s)')
    plt.ylabel('V')
    plt.plot(t,V[i],label='Total Voltage')
    plt.plot(t,VC[i],ls='dotted',label='Voltage in Condensator')
    plt.plot(t,VL[i],ls='dotted',label='Voltage in Coil')
    plt.legend(bbox_to_anchor=(1,1))
    plt.grid()
    plt.show()

# plt.title('$\omega$ = {:.2f} Hz'.format(omega_0))
# plt.xlabel('t(s)')
# plt.ylabel('V')
# plt.plot(t,Voltages(omega_0,R,L,C,t)[0],label='Total Voltage')
# plt.plot(t,Voltages(omega_0,R,L,C,t)[1],ls='dotted',label='Voltage in Condensator')
# plt.plot(t,Voltages(omega_0,R,L,C,t)[2],ls='dotted',label='Voltage in Coil')
# plt.legend(bbox_to_anchor=(1,1))
# plt.grid()
# plt.show()

Resonance frequency = 3162 Hz

Resonance frequency = 3162 Hz

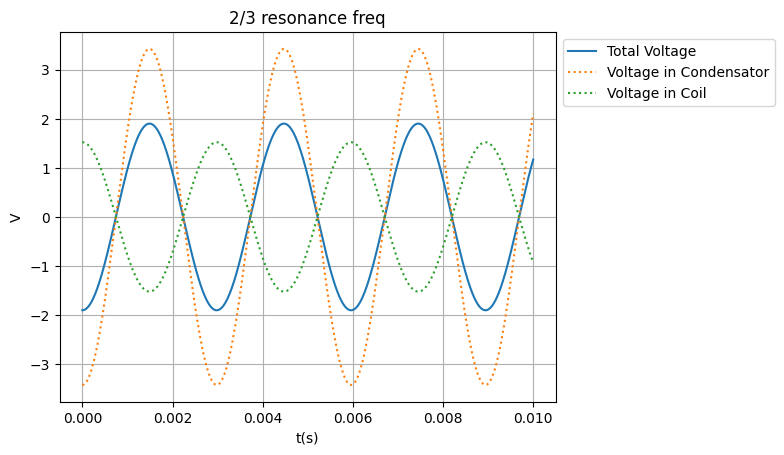
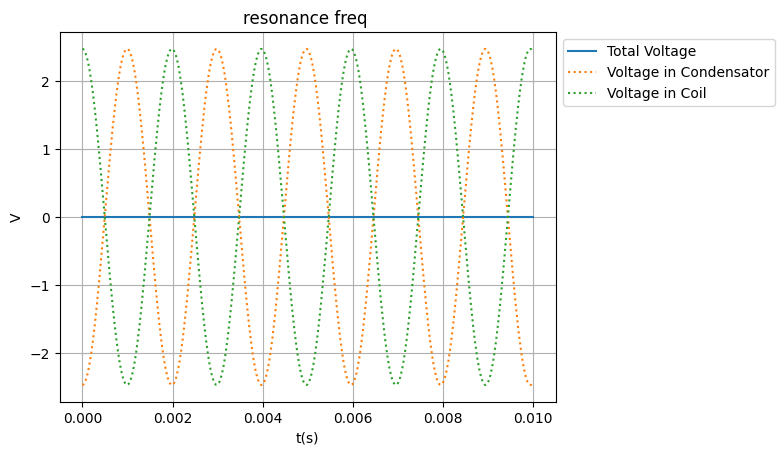
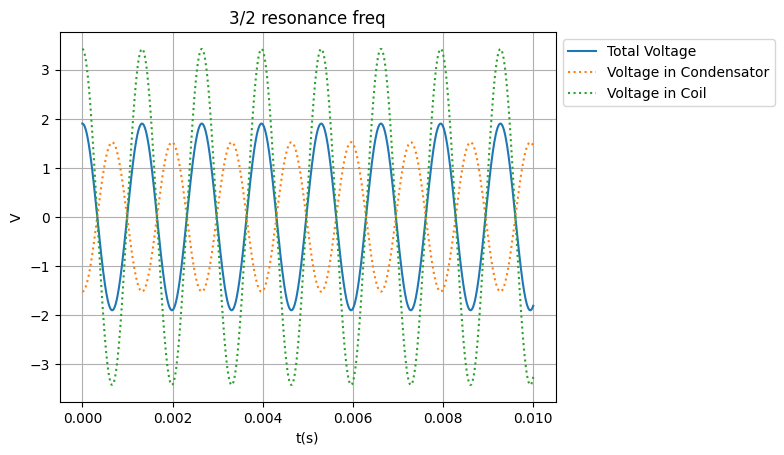
In de grafieken hierboven kunnen we zien dat wanneer we onder de resonantie frequentie zitten, de condensator domineert, en wanneer we boven de resonantie frequentie zitten de spoel domineert. Ook zie je, dat wanner we de resonantie frequentie aanleveren, het totale voltage gelijk aan 0 is.

9.7. Samenvatting wisselstroomschakelingen

Samenvatting van het hoofdstuk over wisselstroomschakelingen.