7. Magnetisme#
7.1. Magnetisme en Lorentzkracht#
Waar elektrische velden veroorzaakt worden door elektrische ladingen en hier op krachten op uitoefenen, geldt die voor magnetische velden bij bewegende elektrische ladingen. Het magnetische veld oefent de zogenaamde Lorentzkracht uit op een bewegende elektrische lading.
Geladen bewegende deeltjes in een homogeen magnetisch veld maken een cirkelbeweging door de Lorentzkracht. Deze cyclotronbeweging is essentieel voor deeltjesversnellers en verplaatsing van geladen deeltjes zoals positronen.
Omdat de straal van de cyclotronbeweging afhangt van de massa van een geladen deeltje, kan deze massa’s onderscheiden in een massaspectrometer, die gebruikt wordt om de structuur van moleculen te bepalen.
Macroscopisch is de Lorentzkracht te meten op stroomdraden waar een flinke stroom door loopt. Dit effect staat aan de basis van de definitie van de stroomeenheid de Ampere.
7.2. Hall effect#
Een magneetveld op een geleider waar een stroom door loopt zal een kracht loodrecht op deze stroom. Deze kracht resulteert in een potentiaal waardoor het mogelijk is om door deze te meten de sterkte van het magneetveld te bepalen.
7.3. Oorzaak magnetische velden#
De wet van Biot-Savart beschrijft hoe een stroom een magnetisch veld genereert.
Door de wet van Biot-Savart te integreren is het mogelijk om het magnetische veld om een oneindig lange stroomdraad te berekenen. Dit doen we eerst analytisch.
7.4. De wet van Biot-Savart, numeriek benaderd voor een oneindig lange draad#
We gaan laten zien, dat de numerieke oplossing van Biot-Savart voor een draad, gelijk is aan de wiskundige berekening.
7.4.1. De wet van Biot-Savart#
De wet van Biot-Savart luidt:
We definiëren een oneindige één-dimensionale draad. Waar we vervolgens het \(\vec{B}\)-veld omheen gaan berekenen. Met de wet van Biot-Savart (in de cel hierboven gegeven), kunnen we de invloed van een klein stukje draad \(dl\) berekenen op het \(\vec{B}\)-veld op het punt \(r\). Het kleine stukje draad draagt heeft een richting, dat is de richting van de stroom.
We gaan het uitproduct uitsplitsen;
Onze draad definiëren we als een oneindige draad in alleen de x richting, oftewel \(d\vec{l}\) heeft alleen een \(x\)-component. Dus we kunnen de wet van Biot-Savart simplificeren. Hierbij maken we gebruik van he volgende:
Zodat we Biot-Savart als volgt kunnen omschrijven:
import numpy as np
import matplotlib.pyplot as plt
def BiotSavart(I,dl,y,z,xc,yc,zc):
# I the current, and dl the piece of wire
# y and z are coordinates at which the magnetic-field is calculated. Recall that our wire is only in the x-direction
# as such, we do not have to calculate x
# xc, yc, zc are coordinates at which the wire is located
rx = xc
ry = (y-yc)
rz = (z-zc)
r=np.sqrt(rx**2 + ry**2 + rz**2)
dBy = -(mu_0/(4*np.pi))*(I*dl*rz/(r**3))
dBz = (mu_0/(4*np.pi))*(I*dl*ry/(r**3))
return dBy,dBz
7.4.2. Berekening van het \(\vec{B}\)-veld#
Nu gaan we \(\vec{B}\) grafisch weergeven. Dit gaan we doen door voor elk stukje \(dl\) te bekijken wat voor een \(d\vec{B}\)-veld dat stukje draad geeft. Vervolgens sommeren we over elke \(d\vec{B}\) om zo vervolgens bij de totale \(\vec{B}\) te komen.
Daarvoor definiëren we de constanten uit de wet van Biot-Savart.
mu_0 = 4*np.pi*1e-7 # N/A^2
I = 10 # A
# First we are going to initialise a grid for calculating B (note it is similar to the dipole grid)
# number of points in grid (along 1 axis)
N=50
# number of points on wire for integration, with more points you obtain a better match to the analytical solution
Nw = 500
# Edges of grid in m
d = 0.01 # m
y_max = d
z_max = d
y_min = -d
z_min = -d
# Grid points
ny = np.linspace(y_min, y_max, N)
nz = np.linspace(z_min, z_max, N)
# Our grid coordinates
y,z = np.meshgrid(ny,nz)
# Now our wire
l = np.linspace(-5*d,5*d,Nw)
# Define the length of a smal piece of the wire
dl = np.abs(l[1]-l[0])
# Now we are going to sum over all dB's:
# First: Define empty B's
By = np.zeros((N,N))
Bz = np.zeros((N,N))
# Then: Calculate our B-fields, by summing all dB's:
for i in range(0,Nw):
dB = BiotSavart(I,dl,y,z,l[i],0,0)
By += dB[0]
Bz += dB[1]
7.4.3. Weergave van het \(\vec{B}\)-veld#
Nu gaan we een vectorplot maken, waarin de pijlen de richting en grootte van het \(\vec{B}\)-veld aangeven.
Net zoals bij het \(\vec{E}\)-veld, schalen we de pijlen, omdat ze er anders gek gaan uitzien als we dichtbij de draad komen. Je kan de code voor die schaling uitzetten, door in de plot Byl en Byz te veranderen in By en Bz respectievelijk, op die manier kan je de grootte van het \(\vec{B}\)-veld in de pijlen kan zien.
# First the actual size of our B-field
B=np.sqrt(By**2 + Bz**2)
# Now for the scaling:
Bmax=np.amax(B)
Bmin=np.amin(B)
scale = np.log(1000*B/Bmin)/B # factor of 1000 increases lengths of lowest E-fields to visibility
Byl=By*scale
Bzl=Bz*scale
# Now for the plot:
fig = plt.figure(figsize=(10, 10))
ax = fig.subplots()
# We make the levels of our contour plot in geomspace, so they are nice and spaced
levels = np.geomspace(Bmin,Bmax,11)
# The wire itself is shown with a red dot
plt.quiver(y,z,Byl,Bzl)
plt.plot(0,0,color='red',marker='o')
plt.contour(y,z,B,levels=levels)
ax.set_xlabel('y [m]')
ax.set_ylabel('z [m]')
ax.set_title('B-field direction, and contours')
ax.set_aspect('equal', adjustable='box')
plt.show()
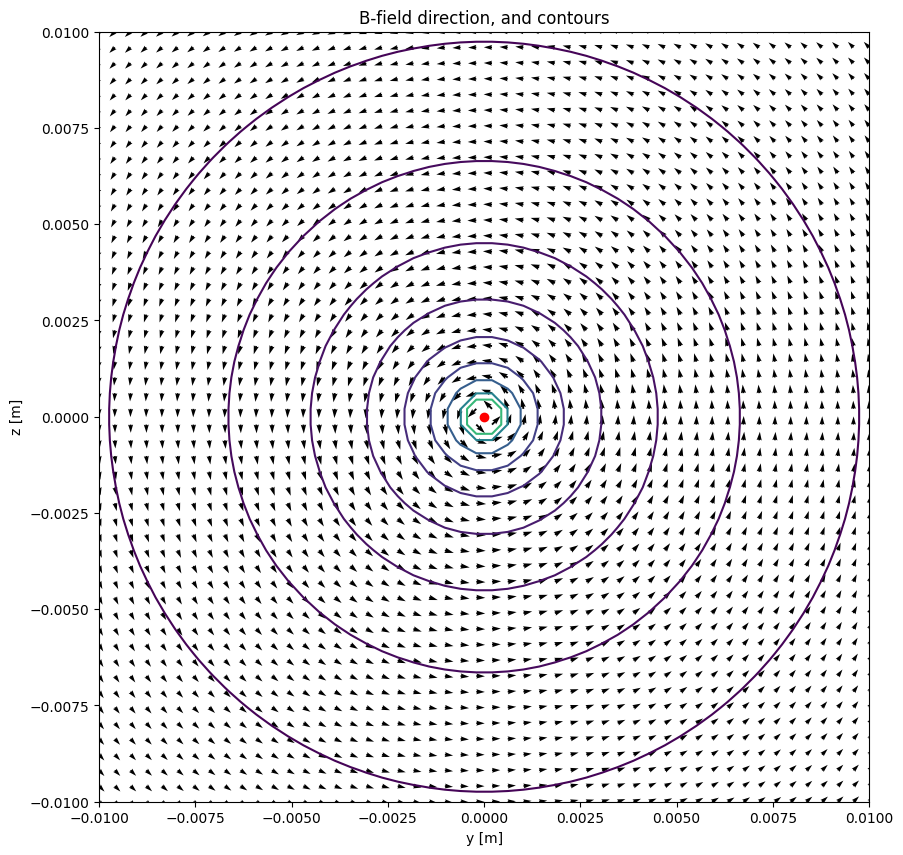
In de bovenstaande plots, zien we dat het \(\vec{B}\)-veld roteerd om de draad. Dit kan je zien, doordat de richting van het \(\vec{B}\)-veld altijd parallel is aan de contour.
7.5. Vergelijking met analytische berekening van het \(\vec{B}\)-veld#
We kunnen berekenen, dat voor een oneindig lange draad geldt:
Waar \(r\) de afstand is tot de draad. We zullen laten zien dat dat hetzelfde is als hetgeen we hierboven hebben laten zien, door te kijken naar de grote van het magnetisch veld op delijn \( z = 0\).
def Bwire(I,y,z,yc,zc):
ry = (y-yc)
rz = (z-zc)
r=np.sqrt(ry**2 + rz**2)
B = (mu_0*I)/(2*np.pi*r)
return B
7.5.1. Weergave verschil wiskundige en numerieke berekening \(\vec{B}\)-veld#
Nu gaan we een plot maken door het midden, \(y=0\), waarin de grootte van het B-veld, zoals berekend met de wiskundige methode, en de numerieke methode. Op deze manier kunnen we het verschil (of gebrek daaraan) tussen de twee technieken laten zien.
# We use exactly the same parameters
B_wire = Bwire(I,ny,0,0,0)
# Define empty B's
By = np.zeros((N))
Bz = np.zeros((N))
# Calculate our B-fields
for i in range(0,Nw):
dB = BiotSavart(I,dl,ny,0,l[i],0,0)
By += dB[0]
Bz += dB[1]
B=np.sqrt(By**2 + Bz**2)
fig = plt.figure(figsize=(10, 10))
ax = fig.subplots()
plt.plot(ny,B,label='numerical calculation')
plt.plot(ny,B_wire,label='mathematical derivation')
ax.set_xlabel('y [m]')
ax.set_ylabel('B [T]')
plt.legend()
plt.show()

Je kan zien, dat, door het eerst wiskundig te berekenen, de code een stuk makkelijker wordt, en ook een stuk sneller!
7.6. Magnetisch veld enkele stroomlus#
De wet van Biot-Savart passen we hier toe op een belangrijke magneetveldbron: de enkele stroomlus.
Het opgewekte veld is wiskundig geheel analoog aan de dipool. In het magnetisme zijn geen monopolen bekend zoals bij elektrische velden, maar wel dipolen.
7.7. Wetten van Maxwell voor magneetvelden#
Door beter te kijken naar de analogie tussen elektrische en magnetische velden is het mogelijk ook een analoge wet van Gauss te formuleren. Deze wet is ook wel de tweede wet van Maxwell genoemd. Dit geeft weer nieuwe methodes om handig magnetische velden te beschouwen.
Door deze wet te beschouwen met de wet van Biot-Savart is het mogelijk om de wet van Ampere af te leiden. Hiermee is het mogelijk om bij symmetrische stroomverdelingen handig magneetvelden uit te rekenen. Deze wet wordt ook wel de vierde wet van Maxwell genoemd.
Als belangrijk voorbeeld gebruiken we hier de wet van Ampere om het magnetische veld van een spoel uit te rekenen. De spoel speelt een grote rol in AC-schakelingen, waar we in de volgende hoofdstukken op in gaan.