3. Elektrische potentiaal

Bij statische ladingsverdelingen in de ruimte zijn de elektrische krachten conservatief, net zoals de zwaartekracht. Dat betekent dat er een potentiaal gedefinieerd kan worden. Via de potentiaal is het vaak makkelijker om een elektrisch veld te berekenen. Het beschouwen van een potentiaal geeft ook nieuwe inzichten in elektrische velden in de buurt van geleiders.

3.1. Potentiaalverschillen

Door de arbeid te beschouwen op een lading in een elektrisch veld, is het mogelijk om de potentiële energie te berekenen en hiermee een elektrische potentiaal te definiëren.

Deze demonstratie met de van der Graaf-generator laat zien in welke richting de elektrische veldlijnen staan. De demonstratie laat ook zien dat de potentiaal ook arbeid kan verrichten.

3.2. Berekenen van de potentiaal

We beschouwen eerst de potentiaal in een uniform elektrisch veld. Daarmee krijgen we inzicht in equi-potentiaallijnen. Vervolgens berekenen we de potentiaal van een enkele puntlading. Hierbij kunnen we ook het nulpunt van een potentiaal definiëren.

3.3. Superpositie en continue ladingsverdelingen

De uitdrukking van de potentiaal van een puntlading is de basis voor het berekenen van veel complexere configuraties via superpositie.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
from matplotlib.cm import ScalarMappable
from matplotlib.colors import Normalize

3.4. Voorbeeld: elektrisch veld van een dipool berekenen via de potentiaal

Een elektrische dipool bestaat uit een positieve lading \((+q)\), en een negatieve \((-q)\) die een afstand d van elkaar verwijderd zijn. Wij zijn geïnteresseerd in de potentiaal op een punt \(P\).

Het eerste wat we bij potentialen altijd moeten definiëren, is op welk punt deze 0 is. De potentiaal op punt \(P\) is namelijk evenredig met de energie die het kost om een deeltje (met een lading) vanuit de plek waar de potentiaal 0 is, naar het punt \(P\) te brengen. Omdat we hier te maken hebben met puntladingen, kunnen we stellen dat de potentiaal in het oneindige 0 is. Onthoud: de elektrisch potentiaal gaat als \(\frac{1}{r}\) .

Omdat we met maar twee puntladingen te maken hebben, is het handig om het principe van superpositie toe te passen:

\[ V(r) = \sum_i \frac{k q_i}{r_i} \]

def Potential(x,y,xc,yc,q):
    # x and y are coordinates at which the potential is calculated
    # xc and yc are coordinates at which the charge is located with the charge q
    rx=(x-xc)
    ry=(y-yc)
    r=np.sqrt(rx**2 + ry**2)
    V = k*q/r
    return V

Je kan in de code hieronder de ladingen en posities van de verschillende deeltjes veranderen, om te zien wat voor invloed ze hebben op de fysieke wereld. De kleurenschaal bij de plots geven de hoogte van de potentiaal weer.

k = 9e9 # N m^2 / C^2
e = 1.6e-19 # Coulomb

# Charges
q_el = -e # an electron
q_po = e # a positron

# Positions of charges
x_el = 50e-12  # m
y_el = 0       # m
x_po = -50e-12 # m
y_po = 0       # m

We definiëren een rooster, waarin we de potentiaal kunnen berekenen.

# Number of points in grid (along 1 axis)
N = 50

# Edges of grid
x_max = 100e-12   # m
y_max = 100e-12
x_min = -100e-12
y_min = -100e-12

# Grid points
nx = np.linspace(x_min, x_max, N)
ny = np.linspace(y_min, y_max, N)

# Our grid coordinates
x,y = np.meshgrid(nx,ny)

# Our potentials.  
V_el = Potential(x,y,x_el,y_el,q_el)
V_po = Potential(x,y,x_po,y_po,q_po)

V = V_el + V_po

3.4.1. Grafische weergave potentiaal

We zullen op twee manieren de potentiaal weergeven: een 2D contourplot en een 3D oppervlakteplot.

fig = plt.figure(figsize=(20,10))

V_min = np.round(V.min())
V_max = np.round(V.max())

levels = np.linspace(V_min,V_max,101)
xp=x*1e12
yp=y*1e12

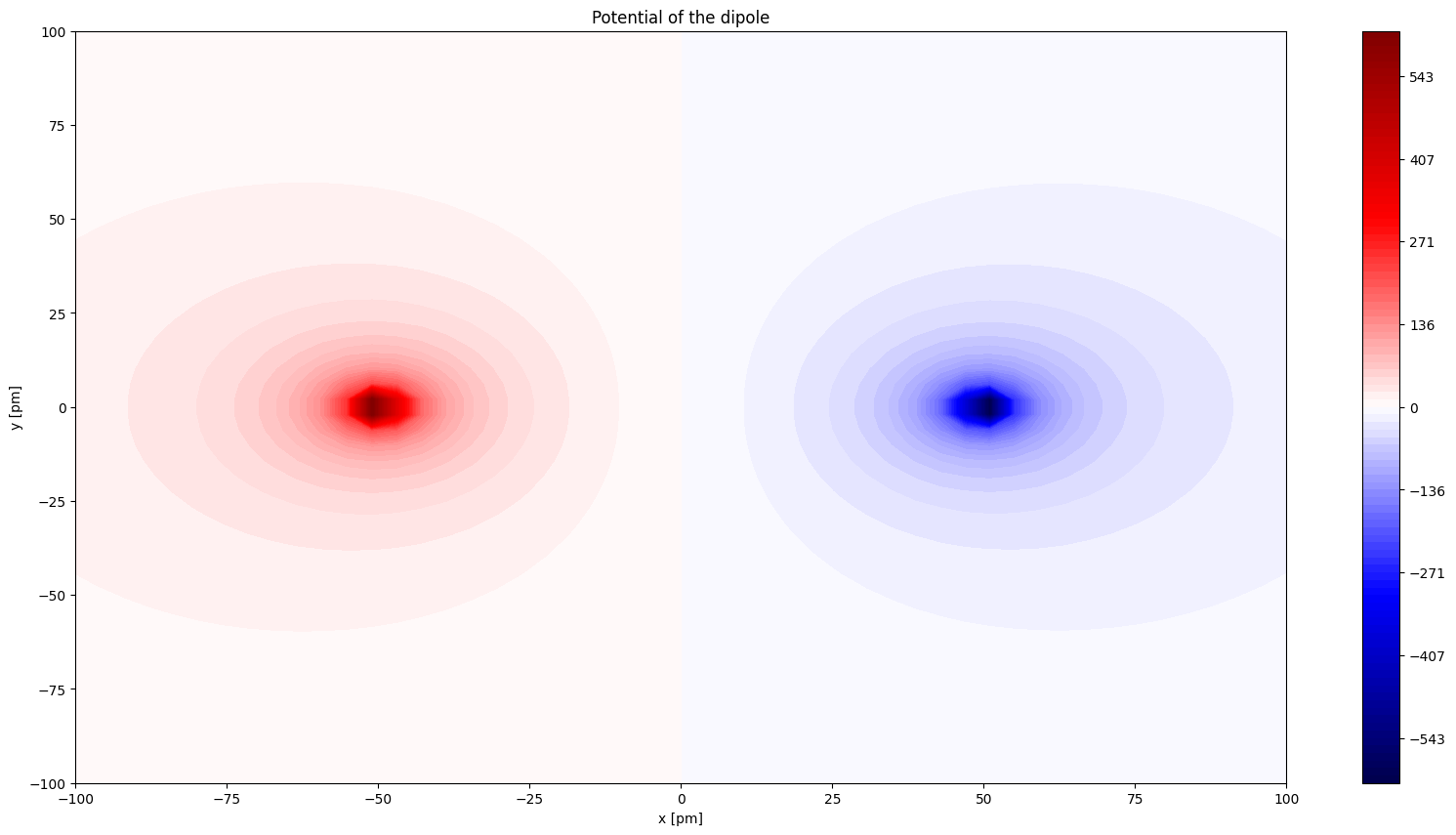
plt.contourf(xp,yp,V,levels=levels,cmap='seismic')
plt.colorbar()

plt.xlabel('x [pm]')
plt.ylabel('y [pm]')

plt.title('Potential of the dipole')

plt.show()

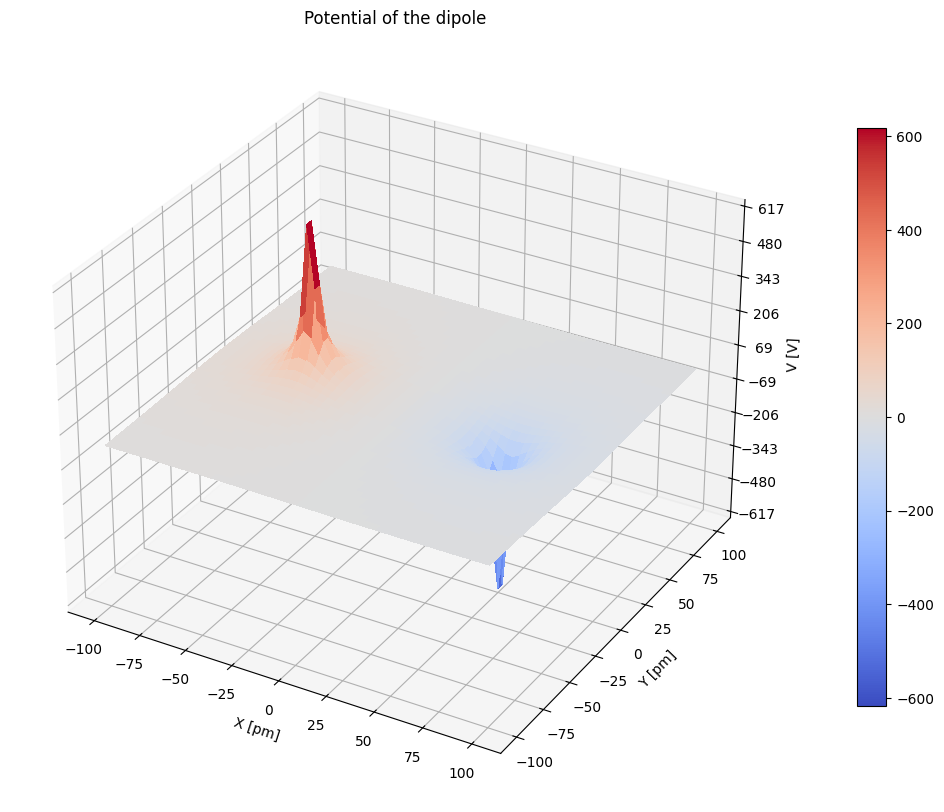
3.4.2. 3D-weergave potentiaal

De 3D plot geeft een indicatie hoe potentiaal werkt: een positieve lading in deze potentiaal gedraagt zich als een bol in een heuvellandschap, waar de heuvels de potentialen zijn. Een negatieve lading zou een bal zijn met negatieve massa! Die gaat dus naar de top van de heuvel.

fig = plt.figure(figsize=(20, 10))
ax = fig.add_subplot(111, projection='3d')
# Plot the surface.
surf = ax.plot_surface(xp, yp, V, cmap=cm.coolwarm, linewidth=0, antialiased=False)
# Customize the z axis.
ax.zaxis.set_major_locator(LinearLocator(10))
ax.set_title('Potential of the dipole')
ax.set_xlabel('X [pm]')
ax.set_ylabel('Y [pm]')
ax.set_zlabel('V [V]')
# Add a color bar which maps values to colors.
fig.colorbar(cm.ScalarMappable(cmap=cm.coolwarm,norm=Normalize(vmin=V.min(),vmax=V.max())),ax=ax,shrink=0.75)
plt.show()

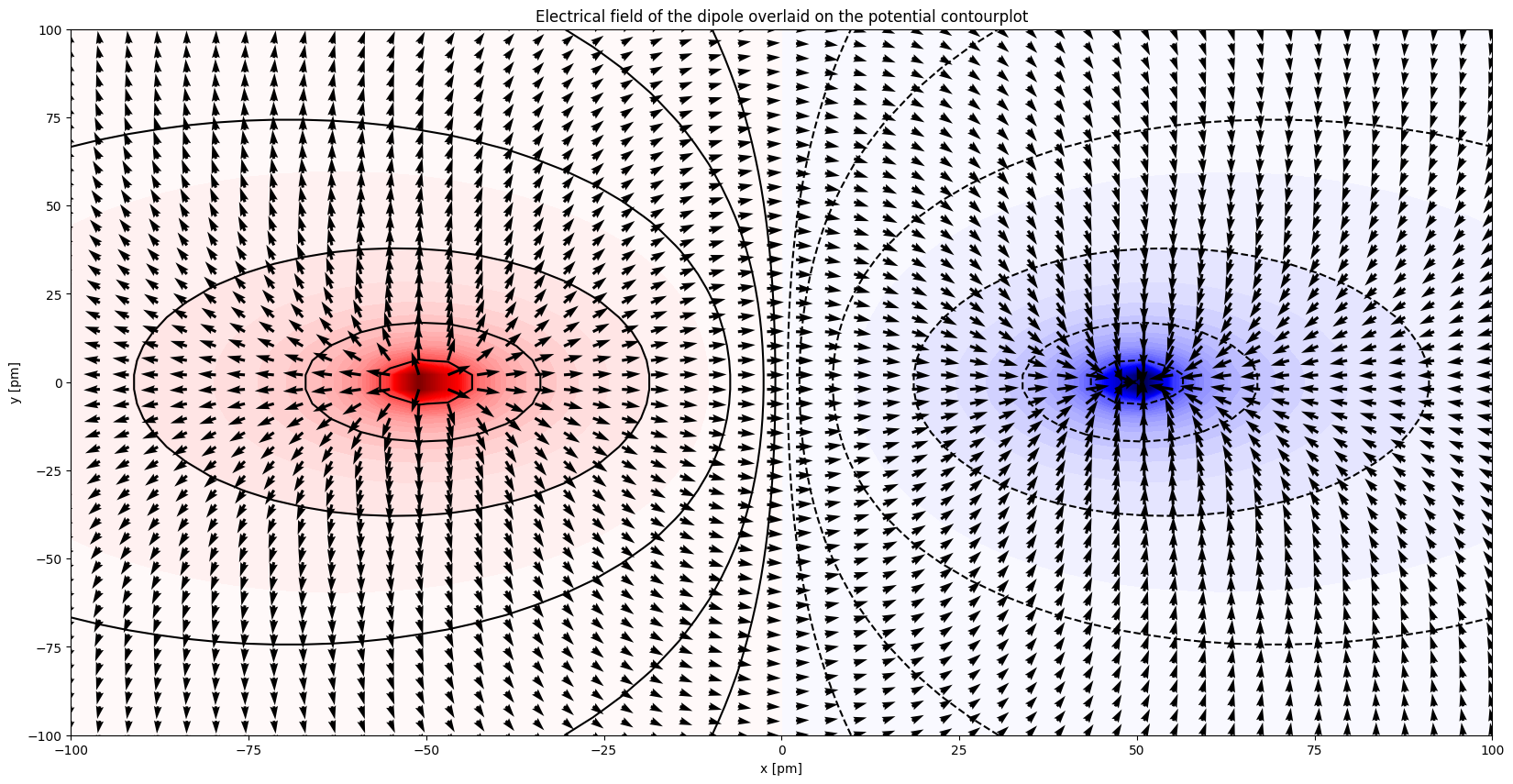
3.5. Elektrisch veld

3.5.1. Elektrisch veld van een potentiaal

Het elektrisch veld kunnen we met behulp van de gradiënt van de potentiaal berekenen. Namelijk:

\[ \vec{E} = -\vec{\nabla}V \]

Oftewel:

\[ E_{x} = -\frac{\partial V}{\partial x} \]

Hetzelfde geldt voor de \(\hat{y}-\) en \(\hat{z}-\) richtingen. Het elektrische veld op deze manier berekenen is simpeler dan direct met de wet van Coulomb, aangezien we pas in de laatste stap vectoren gebruiken.

Je zult zien dat de richting van het \(\vec{E}\)-veld aangeeft in welke richting een positieve lading zou bewegen.

# First we simply calculate E, note we do not yet use the minus gradient, this is done later.
# Furthermore, see that we use the acutal physical V, and not the scaled V.
E = np.gradient(V)

# We split the x and y directions for plotting, see here that we take the negative of the gradient
E_x = -E[1]
E_y = -E[0]

# We  scale the E-field logaritmically to make it visible
E_scale=np.sqrt(E_x**2 + E_y**2)
Emin=np.amin(E_scale)
scale = np.log(1000*E_scale/Emin)/E_scale
El_x = scale*E_x
El_y = scale*E_y

# Plotting
fig = plt.figure(figsize=(20, 10))
ax = fig.subplots()

plt.contourf(xp,yp,V,levels=levels,cmap='seismic')
plt.quiver(xp,yp,El_x,El_y,width=0.002)

# You can see that the E-field is perpendicular to the equi-potential lines
# The dotted line indicates that the potential is negative

# Some nasty tricks are done to show the equi-potential lines in a nice manner
l_pos = np.geomspace(1,V.max(),7)
l_neg = -np.geomspace(-V.min(),1,7)
levels_log = np.concatenate((l_neg,l_pos))
plt.contour(xp,yp,V,levels=levels_log,colors='k')

ax.set_title('Electrical field of the dipole overlaid on the potential contourplot')
ax.set_xlabel('x [pm]')
ax.set_ylabel('y [pm]')
plt.show()

Het superpositieprincipe geldt ook voor de potentiaal. Dit maakt het mogelijk om ook de potentiaal van continue ladingsverdelingen te berekenen.

Als voorbeeld van superpositie spelen we hier met een physlet door een dipool te maken. Probeer het zelf ook uit.

Als voorbeeld berekenen we het elektrisch veld van een geladen ring via de potentiaal. Het begin hiervan is veel eenvoudiger dan via de wet van Coulomb, omdat er alleen met scalairen wordt gewerkt. Vergelijk dit met de eerdere berekening in het eerdere hoofdstuk.

3.6. Potentiaal en veld om een geleider

Via de potentiaal kan je uitspraken doen over het elektrische veld om een geleider.

3.7. Samenvatting elektrostatica

Er zijn meerdere methodes om elektrische velden te berekenen, die ieder hun voor- en nadelen hebben.