1. Elektrische lading, krachten en velden

In dit hoofdstuk laten we zien hoe je met de wet van Coulomb de krachten tussen elektrische ladingen kan uitrekenen. Deze krachten kan je vervolgens beschrijven aan de hand van de elektrische velden veroorzaakt door een lading. De wet van Coulomb is niet alleen geldig voor puntladingen, maar kan ook voor continue verdelingen worden uitgerekend.

1.1. De wet van Coulomb voor puntladingen

De analogie met zwaartekracht kan je gebruiken om zowel elektrische lading als de kracht tussen puntladingen uit te leggen.

Als toepassing van de wet van Coulomb rekenen we de verhouding uit tussen de elektrische en zwaartekracht tussen een elektron en proton uit.

1.2. Superpositie

Elektrische velden kan je simpelweg bij elkaar optellen. We noemen dit principe superpositie.

Als voorbeeld berekenen we de totale kracht die twee regendruppels op een derde uitoefenen.

Om gevoel te krijgen voor superpositie kunnen jullie hierboven kijken naar een spel waarin dit principe wordt toegepast. Het is natuurlijk nog leuker om dit zelf te spelen.

Een van de belangrijkste toepassingen van superpositie is het geval van de dipool. Dipolen komen heel veel voor in de natuur. Veel van de interacties tussen moleculen worden met dipolen beschreven.

1.3. Elektrisch veld van water

1.3.1. Wet van Coulomb herschreven

Als toepassing van de wet van Coulomb en illustratie van superpositie berekenen we het elektrische veld van het watermolecuul.

\[ \vec{E} = \sum_i \frac{k q_i}{r_i^2} \hat{r_i} \]

Waarin \(r_i\) de coördinaten van de atomen beschrijft en \(q_i\) hun lading. Om de \(x\)- en \(y\)-componenten handig te berekenen, herschrijven we de wet van Coulomb:

\[ E_x = \sum_i \frac{k q_i r_x}{r_i^3} \, \]

en

\[ E_y = \sum_i \frac{k q_i r_y}{r_i^3} \, \]

import numpy as np
import matplotlib.pyplot as plt

def LawCoulomb(x,y,xc,yc,q): 
    # x and y are coordinates at which field is calculated
    # xc and yc are coordinates at which the charge is located with the charge q
    k=9e9 # N m^2 / C^2
    rx=(x-xc)*1e-12 # convert from pm to m
    ry=(y-yc)*1e-12 # convert from pm to m
    r=np.sqrt(rx**2 + ry**2)
    Ex=k*q*rx*r**(-3)
    Ey=k*q*ry*r**(-3)
    return Ex, Ey

1.3.2. Structuur van het watermolecuul

We gebruiken de coördinatiehoek en de afstand tussen het zuurstof- en waterstofatoom om de coördinaten in het \(xy\)-vlak te berekenen. We nemen aan dat de elektronen van het waterstofatoom volledig op het zuurstofatoom zitten.

# Charge distribution on H2O
e=1.6e-19 # Coulomb
q_O=-2*e # assume O has 2 extra electrons
q_H1=1*e # assume H hs 1 electron less
q_H2=1*e

# Coordinates H2O
rOH=95.84 # pm
theta=104.45 # degree
theta05=theta*np.pi/360. # theta/2 in radian
x_O=0 # place oxygen at origin
y_O=0
x_H1=-rOH*np.sin(theta05)
y_H1=-rOH*np.cos(theta05)
x_H2=rOH*np.sin(theta05)
y_H2=-rOH*np.cos(theta05)

1.3.3. Elektrisch veld-rooster

We definiëren het rooster om het veld te berekenen in picometer. Het is handig om een even aantal roosterpunten te nemen om te voorkomen dat het zuurstofatoom op een roosterpunt ligt en er een divergentie in de veldberekening optreedt.

# Define lattice for field calculation
nr=50
r_max=500
axis=np.linspace(-r_max,r_max,nr)
x=np.tile(axis,(nr,1))
y=np.tile(axis,(nr,1)).transpose()

1.3.4. Superpositie

We gebruiken het superpositieprincipe om het totale veld te berekenen als de som van de bijdrages van de drie individuele atomen.

# Calculation of the fields of the 3 atoms
[E_Ox,E_Oy]=LawCoulomb(x,y,x_O,y_O,q_O)
[E_H1x,E_H1y]=LawCoulomb(x,y,x_H1,y_H1,q_H1)
[E_H2x,E_H2y]=LawCoulomb(x,y,x_H2,y_H2,q_H2)
Ex=E_Ox+E_H1x+E_H2x # Superposition
Ey=E_Oy+E_H1y+E_H2y

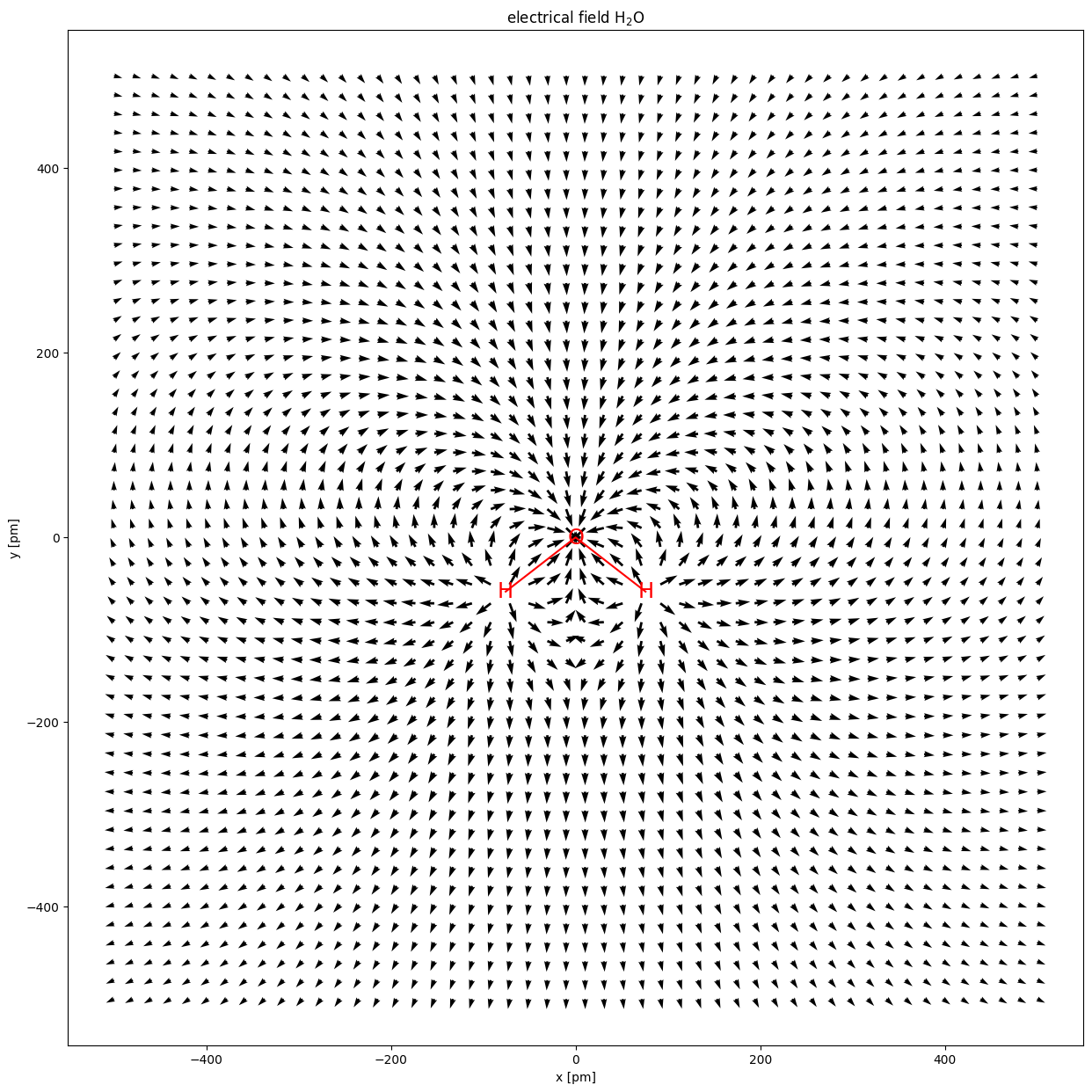
1.3.5. Vectorplot lijkt op dat van een dipool

We plotten de logaritme van de veldsterkte om de richting van zowel de lagere als de hogere velden zichtbaar te maken. Op grote afstanden van het molecuul is het veld gelijk aan dat van een dipool.

#logaritmic scaling of E-field to make it nicely looking
E=np.sqrt(Ex**2 + Ey**2)
Emax=np.amax(E)
Emin=np.amin(E)
scale = np.log(1000*E/Emin)/E # factor of 1000 increases lengths of lowest E-fields to visibility
Exl=Ex*scale
Eyl=Ey*scale
fig = plt.figure(figsize=(15, 15))
ax = fig.subplots()
plt.quiver(x,y,Exl,Eyl)
ax.set_xlabel('x [pm]')
ax.set_ylabel('y [pm]')
ax.set_title('electrical field H$_2$O')
ax.set_aspect('equal', adjustable='box')
ax.text(x_O, y_O, r'O',ha='center',va='center',color='r',fontsize='xx-large') # negative oxygen
ax.text(x_H1, y_H1, r'H',ha='center',va='center',color='r',fontsize='xx-large') # positive hydrogen
ax.text(x_H2, y_H2, r'H',ha='center',va='center',color='r',fontsize='xx-large') # positive hydrogen
plt.plot([x_H1,x_O,x_H2],[y_H1,y_O,y_H2],'r')
plt.show()

1.4. Continue ladingsverdelingen

Veel problemen kan je wiskundig veel makkelijker uitrekenen als je gebruikt maakt van symmetrie. Veel termen kan je vaak op grond van symmetrie weglaten, waardoor berekeningen veel korter worden. Het principe van superpositie kan uitgebreid worden naar continue ladingsverdelingen door over alle lading te integreren.

Als voorbeeld is hier de berekening gegeven van het elektrische veld van een geladen ring met behulp van de wet van Coulomb.

1.5. Integreren in de natuurkunde

We merken dat veel studenten het toepassen van integreren in elektriciteit en magnetisme moeilijk vinden. Integreren in de natuurkunde is vaak over massa of lading in plaats van over ruimtelijke coördinaten, zoals je op de middelbare school met wiskunde gewend bent. Je moet leren om de integraal over bijvoorbeeld lading om te zetten naar een handige ruimtelijke coördinaat. Wat handig is, hangt helemaal af van de geometrie van een probleem. Hieronder geven we drie veel voorkomende voorbeelden van omzettingen van een integratiecoördinaat.

Zo kan je lading bijvoorbeeld over een rechte lijn integreren.

Integreren over een ring of ringsegment is ook mogelijk.

Integreren over een schijf is net wat complexer.

1.6. Demonstratie

De Coulomb-krachten kunnen in een demonstratie goed zichtbaar worden gemaakt.