Stroomschakelingen

6. Stroomschakelingen#

6.1. Wetten van Kirchhoff#

Zowel lading als energie zijn behouden grootheden in stroomschakelingen. In termen van elektromagnetisme zijn dit behoudswetten voor stroom en potentiaal. Deze behoudswetten kan je gebruiken om complexe schakelingen door te rekenen, te bedenken hoe je een schakeling door meet en hoe condensatoren op- en ontladen.

Als je netjes rekening houdt met het teken en de richting van stroom kan je consequent schakelingen doorrekenen. Het maakt helemaal niet uit hoe je de richting kiest als je deze maar consequent vast houdt. In deze video laten we zien hoe je onafhankelijk van je beginkeuzes iedere keer hetzelfde antwoord krijgt.

Dit is een voorbeeld van een berekening van de stroom in verschillende takken van een complexe schakeling. Het belangrijkste bij de uitvoering is om geen kleine rekenfouten te maken.

Het is ook mogelijk om een schakeling na te bouwen met een physlet en dan virtueel de stroom te meten om tot een antwoord te komen.

6.2. Doormeten schakelingen#

Bij het doormeten van een schakeling moet je een spanningsmeter over een element zetten en een stroommeter in een stroomkring. Met de physlet kan je dat goed oefenen.

6.3. Op- en ontladen condensatoren#

Met behulp van de wetten van Kirchhoff kan je uitrekenen hoe een condensator oplaadt en ontlaadt in een stroomkring. Deze wetten leiden tot eenvoudige differentiaalvergelijkingen die een exponentiele functie als oplossing hebben.

6.3.1. Voorbeelden van RC-kringen met verschillende weerstanden#

import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Image

We gaan de stroom door een condensator en het voltage erover berekenen. Wanneer een condensator in een schakeling zit met een batterij en een weerstand is de mate waarin deze op- en ontlaadt afhankelijk van het voltage van de batterij, de grote van de capaciteit van de condensator, maar ook van de grote van de weerstand. Zo’n schakeling heet een RC-kring, en in de meeste simpele vorm ziet het er zo uit:

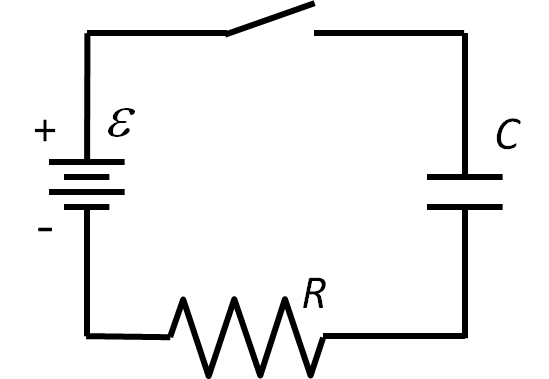
dynamo

We kunnen vervolgens het voltage in, en de stroom door de condensator uitdrukken aan de hand van de volgende twee differentiaal vergelijkingen:

\[ V(t) = \varepsilon\times(1-\exp(\frac{-t}{R C})) \]

voor het voltage in en:

\[ I(t) = \frac{\varepsilon}{R}\times \exp(\frac{-t}{R C}) \]

voor de stroom door de condensator.

We gaan nu kijken wat er gebeurt als we de weerstand in onze schakeling veranderen. Hiervoor kijken we naar de spanning en stroom bij een referentie weerstand en kunnen we zien hoe andere weerstanden zich daar naar verhouden.

We bepalen eerst hoeveel verschillende weerstanden we willen bekijken, en wat onze maximale tijd wordt voor onze plotjes.

N = 4
N_t = 100

R_ref = 10 # Ohm, Reference Resistance
R = np.linspace(1,100,N) # Ohm, Resistance of Resistor
C = 1e-6 #Fahrad, Capacitance of Condensator
E = 10 #Volt, Voltage of battery

We definiëren vervolgens de functie die we gebruiken voor de stroom door en voltage in de condensator.

def CapacitorVI(E,t,R,C):
    Vc = E*(1-np.exp(-t/(R*C)))
    Ic = E*np.exp(-t/(R*C))/R
    return Vc,Ic

We berekenen de stroom en spanning. Wat we hier ook doen is de RC tijd berekenen. De RC tijd is een karakteristieke tijd voor een schakeling, die aangeeft hoe lang het duurt (in seconden), voordat die tot 63,2% is opgeladen (of totdat die tot 36,8% is ontladen als we de condensator ontladen). Dit specifieke percentage komt uit de vergelijking voor de voltage en stroom, i.e. \( 0.632 \approx 1 - e^{-1}\) en \( 0.368 \approx e^{-1}\).

Vc = np.zeros((N,N_t))
Ic = np.zeros((N,N_t))
RC_time = R_ref*C
t = np.linspace(0,5*RC_time,N_t)

for i in range(N):
    Vc[i,:],Ic[i,:] = CapacitorVI(E,t,R[i],C)

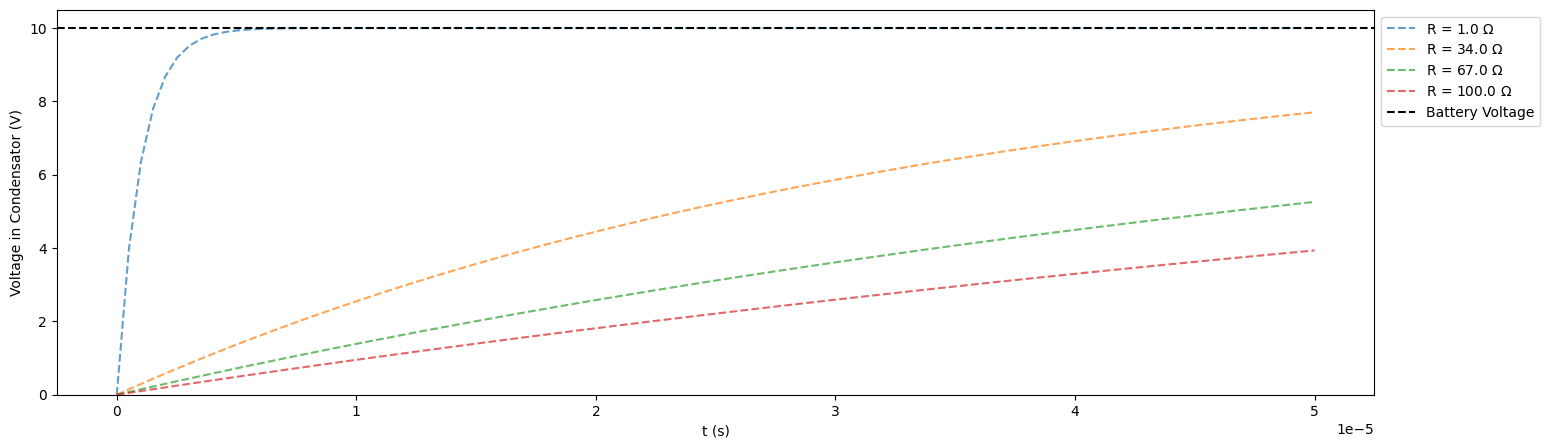
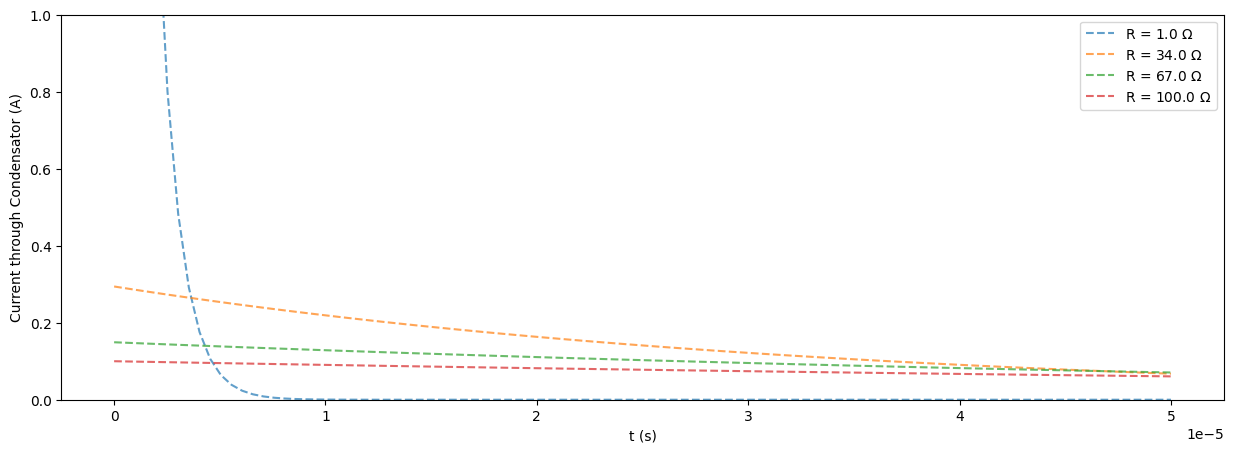
In onderstaande figuren zien we hoe de condensator oplaadt voor verschillende weerstanden. Je kan zien dat hoe kleiner de weerstand is, hoe sneller de condensator oplaadt, en er geen stroom meer door de condensator gaat.

plt.figure(figsize=(17,5))
for i in range(N):
    plt.plot(t,Vc[i],linestyle='dashed',alpha=0.7,label='R = {}'r' $\Omega$'.format(R[i]))
plt.axhline(E,linestyle='dashed',color='black',label='Battery Voltage')
# plt.axvline(RC_time,linestyle='dashed',color='grey')
# plt.axhline(0.632*E,linestyle='dashed',color='grey',label='RC time voltage')
plt.ylim(0,1.05*E)
plt.legend(bbox_to_anchor=(1,1))
plt.xlabel('t (s)')
plt.ylabel('Voltage in Condensator (V)')
plt.show()

plt.figure(figsize=(15,5))
for i in range(N):
    plt.plot(t,Ic[i],linestyle='dashed',alpha=0.7,label='R = {}'r' $\Omega$'.format(R[i]))
plt.ylim(0,E/10.)
plt.legend(bbox_to_anchor=(1,1))
plt.xlabel('t (s)')
plt.ylabel('Current through Condensator (A)')
plt.show()