Numerical differentiation

12. Numerical differentiation#

12.1. Derivative#

In simple words, the derivative of a function can be interpreted as “the rate of change of the function with respect to its variable” or geometrically as “the slope of the curve of the mathematical function f(x) plotted as a function of x”. But why is it so important? Because in nature many physical entities are defined as instantaneous rates of change of some other quantity. Therefore using derivatives s to precise modeling of the desired quantity. Thus, they are fundamental to the solution of problems in calculus and differential equations. However, in many practical problems we may not explicitly know the function, but only a set of data points. For such reasons it may be preferred to compute derivatives numerically rather than analytically.

12.2. Derivative formula#

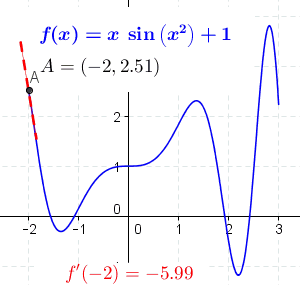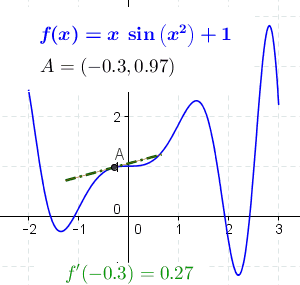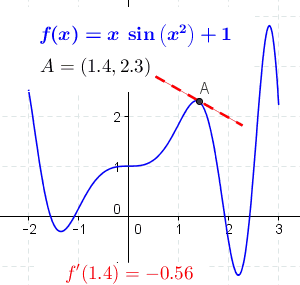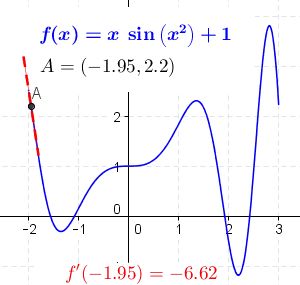
The derivative of a function \(f(x)\) at \(x=a\) is defined by the limit \(f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}\) As an example, the figure below shows the function \(f(x)=x\sin(x^2)+1\) and its derivative at different points. Sine function and derivative

12.3. Finite difference formula#

The finite difference is often used as a numerical approximation of the derivative. Three basic finite different formulas are:

  • A forward difference: \(f'(a) \approx \frac{f(a + h) - f(a)}{h}\)

  • A backward difference: \(f'(a) \approx \frac{f(a) - f(a - h)}{h}\)

  • Central difference: \(f'(a) \approx \frac{1}{2} \left( \frac{f(a + h) - f(a)}{h} + \frac{f(a) - f(a - h)}{h} \right) = \frac{f(a + h) - f(a - h)}{2h}\)

These three approaches are demonstrated in the picture below. You can use any of these equations; whichever suits your application better.

Finite difference method

12.4. Finite difference in Python#

The function below uses the finite difference equations introduced above to compute the difference formula for \(f'(a)\) with step size \(h\).

import numpy as np
import matplotlib.pyplot as plt

def my_derivative(f,method,a,h):

    if method == 'central':
        return (func(a + h) - func(a - h))/(2*h)
    elif method == 'forward':
        return (func(a + h) - func(a))/h
    elif method == 'backward':
        return (func(a) - func(a - h))/h
    else:
        raise ValueError("Method should be 'central', 'forward' or 'backward'.")

12.5. Some examples#

Below are some examples.

12.5.1. Example 1#

Find the derivative of \(f(x) = \sin(x)\) for \(x \in [0, 100]\).

To solve this problem in Python, we use the derivative function to find the derivative of the sine function for all the points. For comparison, we plot the true values using the analytic equation \( \frac{d \sin (x)}{dx}=\cos(x)\).

import numpy as np
import matplotlib.pyplot as plt

# Define your own central difference function
def central_diff(f, x, dx=1e-5):
    return (f(x + dx) - f(x - dx)) / (2 * dx)

# Vectorize it so it works on arrays
vec_central_diff = np.vectorize(lambda x_val: central_diff(np.sin, x_val, dx=0.01))

# x and y values
x = np.linspace(0, 5 * np.pi, 100)
y = np.sin(x)

# Approximate and true derivative
central_diff_vals = vec_central_diff(x)
true_diff = np.cos(x)

# Plot
plt.figure(figsize=(10, 4))
plt.plot(x, y, label='y = sin(x)')
plt.plot(x, central_diff_vals, 'r.', label='Central Difference')
plt.plot(x, true_diff, 'b:', label='True Derivative')
plt.title('Central Difference Derivative of y = sin(x)')
plt.legend(loc='best')
plt.grid(True)
plt.show()
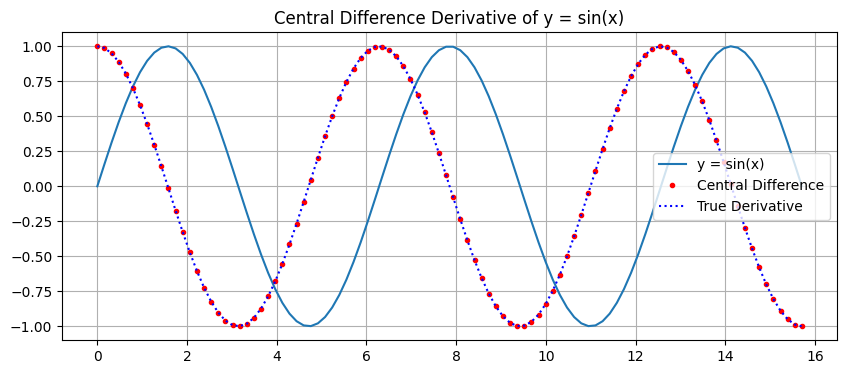
../../../_images/c5ed27b40879c161451a7fecd12c444b1ae8e3a81acc2be62ea4eaa4cc6a86a9.png

12.5.2. Example 2:#

This assignment is dapted from Problem 6.1 in Fundamentals of Electric Circuits (Alexander & Sadiku, 2017).

If the voltage across a \(7.5 F\) capacitor is \(2t\exp^{−3t} V\) , find the current through it at \(t=2 s\).

Hint: \(i(t)=C \frac{dV(t)}{dt}\)

import numpy as np

# Define the function
V = lambda t: 2 * t * np.exp(-3 * t)

# Define central difference derivative function
def central_diff(f, x, dx=1e-5):
    return (f(x + dx) - f(x - dx)) / (2 * dx)

# Use it
x0 = 2
i = 7.5 * central_diff(V, x0, dx=0.01)
print(i)

-0.1859231450781365
Contents