4.3. Application: Graphs#
Generalising from the data structure of a tree, we can create a graph. In computer science, we can model many different problems as graphs: from shortest paths to help your navigation system, to scheduling sports matches. Think of a graph like a tree, except that there can be edges between ‘sibling’ nodes—and more.
4.3.1. Graph nomenclature#
A graph is a 2-tuple of two sets often denoted as \(G = (V,E)\). The first coordinate \(V\) is a set of vertices, also called nodes . The second coordinate \(E\) is a set of edges, where each edge represents a connection between two vertices. Two vertices connected by an edge are called neighbours. Graphically, we often draw vertices as circles with edges as lines between them, as we did for trees in the last chapter. For example consider the following visual representation of a graph \(G_1\):
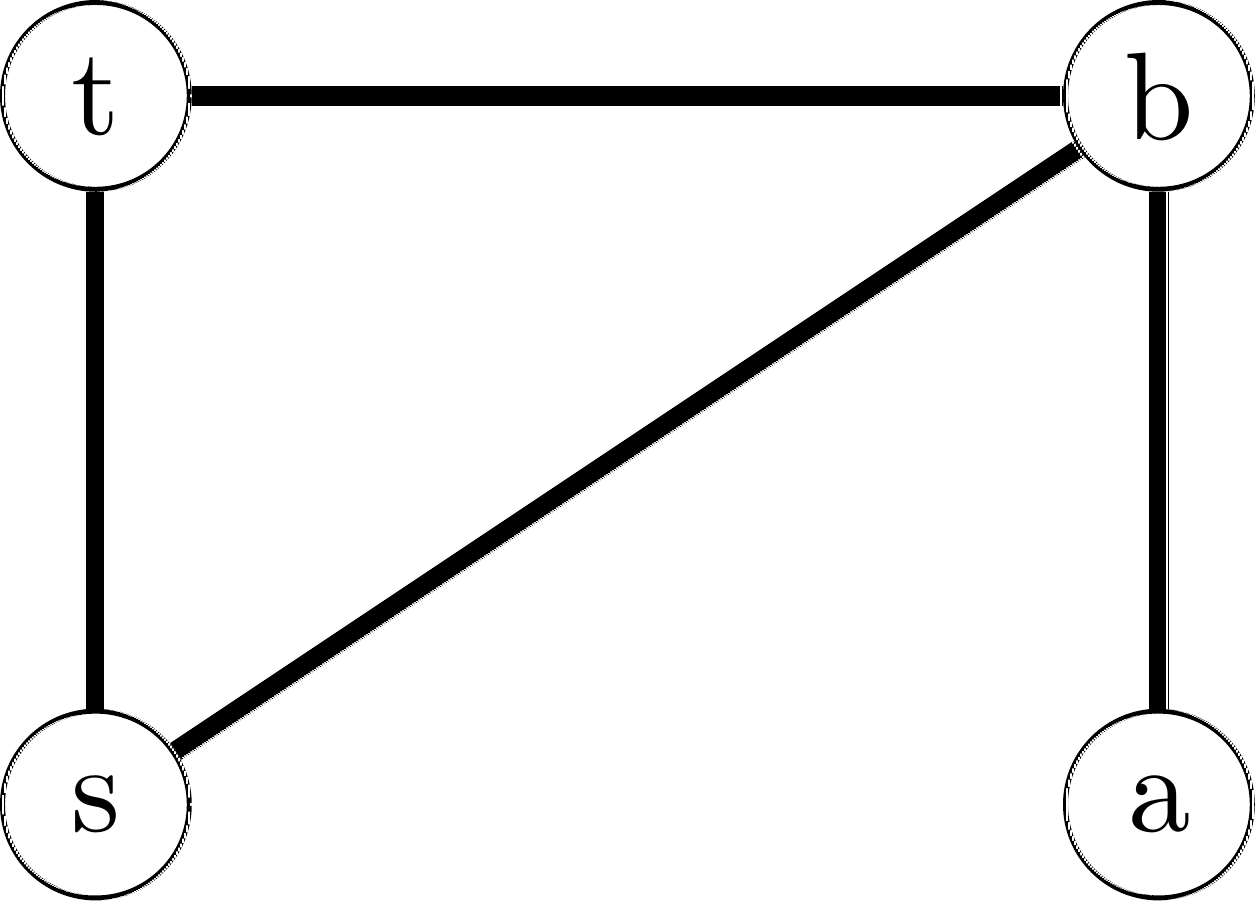
This graph can also be expressed more formally as:
\( G_1 = (\{s, a, b, t\}, \{\{s, t\}, \{s, b\}, \{a, b\}, \{b, t\}\}) \)
This graph is what we call undirected, by which we mean that edges do not have a direction. As a result we represent the edges as sets meaning \(E \subseteq \{\{v_1, v_2\} | v_1 \neq v_2 \wedge v_1, v_2 \in V\}\). In contrast in a directed graph, edges have an origin and a destination. Consider now graph \(G_2\):
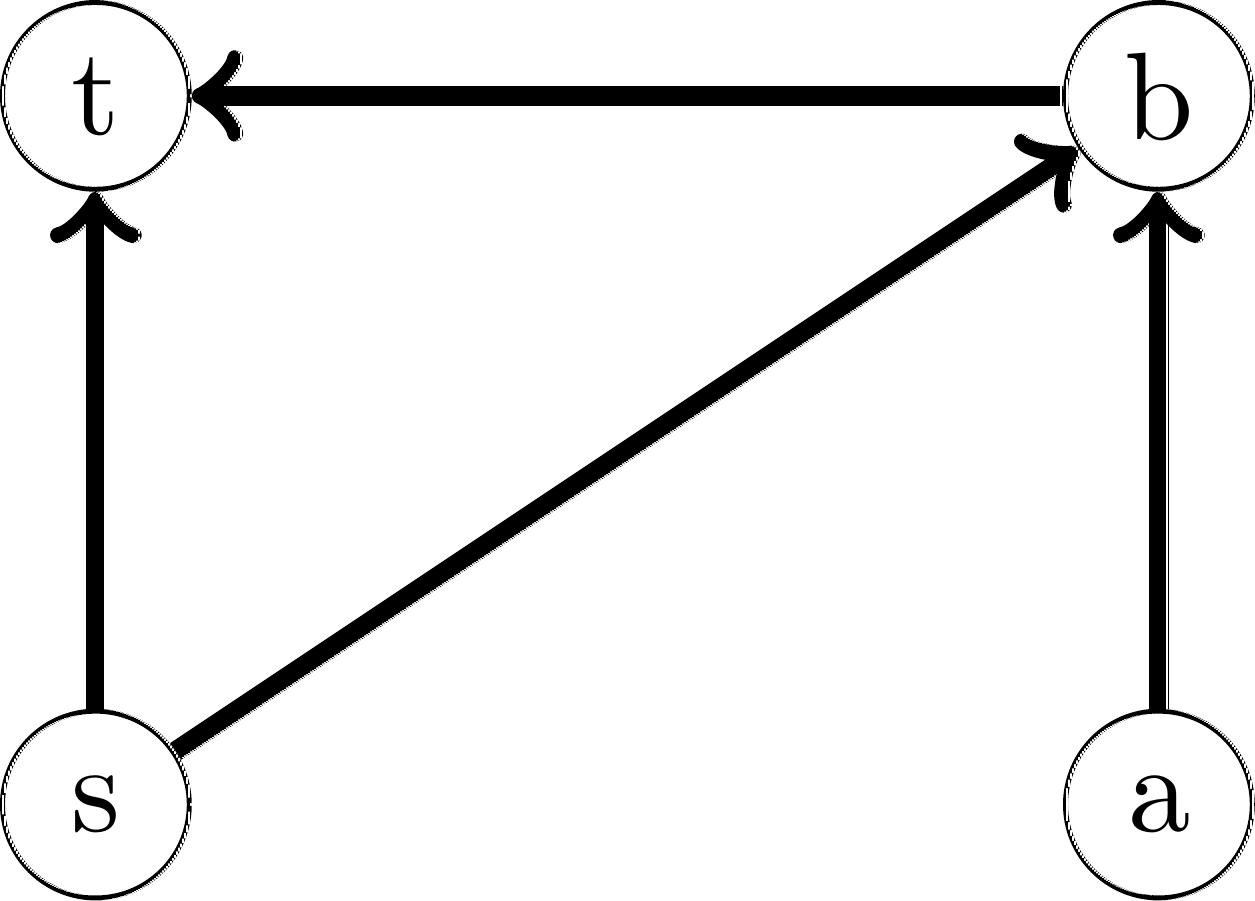
This graph can be expressed as a 2-tuple as:
\( G_2 = (\{s, a, b, t\}, \{(s, t), (s, b), (a, b), (b, t)\}) \)
Notice that for directed graphs it holds that \(E \subseteq V \times V\). Finally we define a path as a sequence of some edges. For example a path \(\pi = ((s,b),(b,t))\) denotes a path from \(s\) to \(t\) in the graph \(G_2\) above.
In Section 4.5.5 we will revisit this model for graphs and explore what the addition of functions can do to enrich our graph model.
4.3.2. An application of graphs: Task ordering#
As you are taking Reasoning & Logic, you have many different tasks that you need to complete. Reading sections from the book, doing book exercises, homework assignments, and of course exams. This can be quite overwhelming, both in figuring out where to start, as well as to figure out what order to complete tasks in. Fortunately you can use a graph to help you structure your tasks!
If you are given a number of tasks you need to do, with precedence constraints between them (for example you need to read the book and watch a video, before doing the homework) as a set of ordered pairs. You can model this problem as a graph, turning tasks into vertices and these precedence constraints into edges. The result may look very similar to those you find on ad-cs.ewi.tudelft.nl! Assuming it is feasible to do the tasks, your graph will be what we call a Directed Acyclic Graph (or DAG). After all, if there is some cycle in your graph, then a task can never be completed! (Do you see why?)
Now to find an order in which the tasks can be completed, we look for what we call a topological ordering. In such an ordering we number the vertices \(v_1\) through \(v_{|V|}\) in such a way that for all edges \((v_x, v_y) \in E\) it holds that \(x < y\). For example, for the graph \(G_2\) in the previous section, \(a, s, b, t\) is a possible topological ordering. A method to find such a topological ordering is as follows:
Pick a vertex without incoming edges.
Add it to the topological ordering, and remove it and its outgoing edges from the graph.
While there are still vertices left, go back to step 1.
In the exercises, you will be asked to write a proof by contradiction to prove that there is always a vertex without incoming edges in a DAG. You will further analyse and also implement this algorithm in the Algorithms & Data Structures course.
4.3.3. Exercises#
Exercise (1)
Draw an undirected graph of \(10\) vertices, so that the longest path in the graph consists of \(6\) edges.
Exercise (2)
Draw a directed acyclic graph of \(8\) vertices, and \(13\) edges.
Exercise (3)
Give a topological ordering of the DAG you drew in the previous exercise.
Exercise (4)
Prove the following claim: ‘’Every DAG has at least one vertex without incoming edges.’’ You may find a proof by contradiction to be useful here.