4.1. Basic Concepts#

A set is a collection of elements. A set is defined entirely by the elements that it contains. An element can be anything, including another set. You will notice that this is not a precise mathematical definition. Instead, it is an intuitive description of what the word ‘set’ is supposed to mean: any time you have a bunch of entities and you consider them as a unit, you have a set. Mathematically, sets are really defined by the operations that can be performed on them. These operations model things that can be done with collections of objects in the real world. These operations are the subject of the branch of mathematics known as set theory.

The most basic operation in set theory is forming a set from a given list of specific entities. The set that is formed in this way is denoted by enclosing the list of entities between a left brace, ‘\(\{\)’, and a right brace, ‘\(\}\)’. The entities in the list are separated by commas. For example, the set denoted by

\[\{\ 17,\ \pi,\ \texttt{New York City},\ \texttt{King Willem-Alexander},\ \texttt{Euromast}\ \}\]

is the set that contains the entities 17, \(\pi\), New York City, King Willem-Alexander, and Euromast. These entities are the elements of the set. Fig. 4.1 is an abstract depiction this set.

Since we assume that a set is completely defined by the elements that it contains, the set is well-defined. Of course, we still haven’t said what it means to be an ‘entity’. Something as definite as ‘New York City’ should qualify, except that it doesn’t seem like New York City really belongs in the world of mathematics. The problem is that mathematics is supposed to be its own self-contained world, but it is supposed to model the real world. When we use mathematics to model the real world, we admit entities such as New York City and even Euromast. But when we are doing mathematics per se, we’ll generally stick to obviously mathematical entities such as the integer 17 or the real number \(\pi\). We will also use letters such as \(a\) and \(b\) to refer to entities. For example, when we say something like ‘’Let \(A\) be the set \(\{a,b,c\}\)’’, we mean \(a\), \(b\), and \(c\) to be particular, but unspecified, entities.

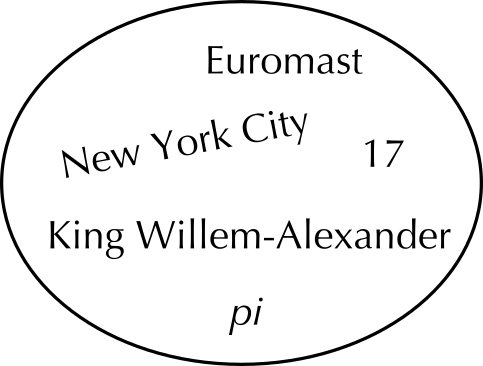
../../_images/our-example-venn.png

Fig. 4.1 Venn diagram of an example set.#

Important

It’s important to understand that a set is defined by the elements that it contains, and not by the order in which those elements might be listed. For example, the notations \(\{a,b,c,d\}\) and \(\{b,c,a,d\}\) define the same set. Furthermore, a set can only contain one copy of a given element, even if the notation that specifies the set lists the element twice. This means that \(\{a,b,a,a,b,c,a\}\) and \(\{a,b,c\}\) specify exactly the same set. Note in particular that it’s incorrect to say that the set \(\{a,b,a,a,b,c,a\}\) contains seven elements, since some of the elements in the list are identical. The notation \(\{a,b,c\}\) can lead to some confusion, since it might not be clear whether the letters \(a\), \(b\), and \(c\) are assumed to refer to three different entities. A mathematician would generally not make this assumption without stating it explicitly, so that the set denoted by \(\{a,b,c\}\) could actually contain either one, two, or three elements. When it is important that different letters refer to different entities, we will say so explicitly, as in ‘’Consider the set \(\{a,b,c\}\), where \(a\), \(b\), and \(c\) are distinct.’’

4.1.1. Elements of sets#

The symbol \(\in\) is used to express the relation ‘is an element of’. That is, if \(a\) is an entity and \(A\) is a set, then \(a\in A\) is a statement that is true if and only if \(a\) is one of the elements of \(A\). In that case, we also say that \(a\) is a member of the set \(A\). The assertion that \(a\) is not an element of \(A\) is expressed by the notation \(a\not\in A\). Note that both \(a\in A\) and \(a\not\in A\) are statements in the sense of propositional logic. That is, they are assertions which can be either true or false. The statement \(a\not\in A\) is equivalent to \(\lnot(a\in A)\).

Tip

As you may have noticed by now, it is convention for sets to be denoted using capital letters (e.g. ‘A’) and elements within sets to be denoted using lowercase letters (e.g. ‘a’). You should adhere to the same convention to prevent misunderstandings!

It is possible for a set to be empty, that is, to contain no elements whatsoever. Since a set is completely determined by the elements that it contains, there is only one set that contains no elements. This set is called the empty set, and it is denoted by the symbol \(\emptyset\). Note that for any element \(a\), the statement \(a\in\emptyset\) is false. The empty set, \(\emptyset\), can also be denoted by an empty pair of braces, i.e., \(\{\) \(\}\).

If \(A\) and \(B\) are sets, then, by definition, \(A\) is equal to \(B\) if and only if they contain exactly the same elements. In this case, we write \(A=B\). Using the notation of predicate logic, we can say that \(A=B\) if and only if \(\forall x(x\in A \leftrightarrow x\in B)\).

Important

Later, when proving theorems in set theory, we will find it can often help to use this predicate logic notation to simplify our proofs. To avoid having to look them up later, make sure that you understand why the predicate logic notation is equivalent to the set notation.

Suppose now that \(A\) and \(B\) are sets such that every element of \(A\) is an element of \(B\).
In that case, we say that \(A\) is a subset of \(B\), i.e. \(A\) is a subset of \(B\) if and only if \(\forall x(x\in A \rightarrow x\in B)\). The fact that \(A\) is a subset of \(B\) is denoted by \(A\subseteq B\). Note that \(\emptyset\) is a subset of every set \(B\): \(x \in \emptyset\) is false for any \(x\), and so given any \(B\), \((x\in \emptyset \rightarrow x\in B)\) is true for all \(x\).

If \(A=B\), then it is automatically true that \(A\subseteq B\) and that \(B\subseteq A\). The converse is also true: If \(A\subseteq B\) and \(B\subseteq A\), then \(A=B\). This follows from the fact that for any \(x\), the statement \((x\in A \leftrightarrow x\in B)\) is logically equivalent to the statement \((x\in A\rightarrow x\in B) \wedge (x\in B\rightarrow x\in A)\). This fact is important enough to state as a theorem.

Theorem 4.1

Let \(A\) and \(B\) be sets. Then \(A=B\) if and only if both \(A\subseteq B\) and \(B\subseteq A\).

This theorem expresses the following advice: If you want to check that two sets, \(A\) and \(B\), are equal, you can do so in two steps. First check that every element of \(A\) is also an element of \(B\), and then check that every element of \(B\) is also an element of \(A\).

If \(A\subseteq B\) but \(A\not= B\), we say that \(A\) is a proper subset of \(B\). We use the notation \(A\varsubsetneq B\) to mean that \(A\) is a proper subset of \(B\). That is, \(A\varsubsetneq B\) if and only if \(A\subseteq B \wedge A\not= B\). We will sometimes use \(A\supseteq B\) as an equivalent notation for \(B\subseteq A\), and \(A\varsupsetneq B\) as an equivalent for \(B\varsubsetneq A\). Other textbooks also sometimes use the \(\subset\) symbol to represent proper subsets, e.g., \(A \subset B \equiv A \varsubsetneq B\). Additionally, you may come across \(A\not\subseteq B\) which means that \(A\) is not a subset of \(B\). Notice that (especially in written text) the difference between \(A \varsubsetneq B\) and \(A\not\subseteq B\) can be small, so make sure to read properly and to write clearly!

4.1.2. Set-builder notation#

A set can contain an infinite number of elements. In such a case, it is not possible to list all the elements in the set: we cannot give an extensional definition of the set. Sometimes the ellipsis ‘… ‘ is used to indicate a list that continues on infinitely. For example, \(\mathbb{N}\), the set of natural numbers, can be specified as

\[\mathbb{N} = \{ 0, 1, 2, 3, ... \}\]

However, this is an informal notation, which is not really well-defined, and it should only be used in cases where it is clear what it means. It’s not very useful to say that ‘’the set of prime numbers is \(\{2,3,5,7,11,13,... \}\)’’, and it is completely meaningless to talk about ‘’the set \(\{17,42,105,... \}\)’’. Clearly, we need another way to specify sets besides listing their elements. The need is fulfilled by predicates.

If \(P(x)\) is a predicate, then we can form the set that contains all entities \(a\) such that \(a\) is in the domain of discourse for \(P\) and \(P(a)\) is true. The notation \(\{x | P(x)\}\) is used to denote this set. This is the intensional definition of the set. The name of the variable, \(x\), is arbitrary, so the same set could equally well be denoted as \(\{z| P(z)\}\) or \(\{r| P(r)\}\). The notation \(\{x| P(x)\}\) can be read ‘’the set of \(x\) such that \(P(x)\)’’. We call this the set-builder notation, as you can think of the predicate as a building material for the elements of the set. For example, if \(E(x)\) is the predicate ‘\(x\) is an even number’, and if the domain of discourse for \(E\) is the set \(\mathbb{N}\), then the notation \(\{x| E(x)\}\) specifies the set of even natural numbers. That is,

\[\{x| E(x)\} = \{0,2,4,6,8,... \}\]

Note

It turns out, for deep and surprising reasons that we will discuss later, that we have to be a little careful about what counts as a predicate.
In order for the notation \(\{x| P(x)\}\) to be valid, we have to assume that the domain of discourse of \(P\) is in fact a set.
(You might wonder how it could be anything else. That’s the surprise!)

Often, it is useful to specify the domain of discourse explicitly in the notation that defines a set. In the above example, to make it clear that \(x\) must be a natural number, we could write the set as \(\{x\in\mathbb{N} | E(x)\}\). This notation can be read as ‘’the set of all \(x\) in \(\mathbb{N}\) such that \(E(x)\)’’. More generally, if \(X\) is a set and \(P\) is a predicate whose domain of discourse includes all the elements of \(X\), then the notation

\[\{x\in X| P(x)\}\]

is the set that consists of all entities \(a\) that are members of the set \(X\) and for which \(P(a)\) is true. In this notation, we don’t have to assume that the domain of discourse for \(P\) is a set, since we are effectively limiting the domain of discourse to the set \(X\). The set denoted by \(\{x\in X| P(x)\}\) could also be written as \(\{x| x\in X\wedge P(x)\}\).

Example

We can use this notation to define the set of prime numbers in a rigorous way. A prime number is a natural number \(n\) which is greater than 1 and which satisfies the property that for any factorization \(n=xy\), where \(x\) and \(y\) are natural numbers, either \(x\) or \(y\) must be \(n\). We can express this definition as a predicate and define the set of prime numbers as

\[\begin{split}\begin{align*} \{ n\in\mathbb{N}| &(n>1)\ \wedge\\ &\forall x\forall y\big((x\in\mathbb{N}\wedge y\in\mathbb{N}\wedge n=xy)\rightarrow(x=n\vee y=n)\big) \} \end{align*}\end{split}\]

Admittedly, this definition is hard to take in in one gulp. But this example shows that it is possible to define complex sets using predicates.

4.1.3. Operations on sets#

Now that we have a way to express a wide variety of sets, we turn to operations that can be performed on sets. The most basic operations on sets are union and intersection. If \(A\) and \(B\) are sets, then we define the union of \(A\) and \(B\) to be the set that contains all the elements of \(A\) together with all the elements of \(B\). The union of \(A\) and \(B\) is denoted by \(A\cup B\). The union can be defined formally as

\[A\cup B = \{x| x\in A \vee x\in B\}.\]

The intersection of \(A\) and \(B\) is defined to be the set that contains every entity that is both a member of \(A\) and a member of \(B\). The intersection of \(A\) and \(B\) is denoted by \(A\cap B\). Formally,

\[A\cap B = \{x| x\in A \wedge x\in B\}.\]

An entity gets into \(A\cup B\) if it is in either \(A\) or \(B\). It gets into \(A\cap B\) if it is in both \(A\) and \(B\). Note that the symbol for the logical ‘or’ operator, \(\vee\), is similar to the symbol for the union operator, \(\cup\), while the logical ‘and’ operator, \(\wedge\), is similar to the intersection operator, \(\cap\).

The set difference of two sets, \(A\) and \(B\), is defined to be the set of all entities that are members of \(A\) but are not members of \(B\). The set difference of \(A\) and \(B\) is denoted \(A\smallsetminus B\) or alternatively as \(A - B\). The idea is that \(A\smallsetminus B\) is formed by starting with \(A\) and then removing any element that is also found in \(B\). Formally,

\[A\smallsetminus B = \{x| x\in A \wedge x\not\in B\}.\]

Union and intersection are clearly commutative operations. That is, \(A\cup B=B\cup A\) and \(A\cap B=B\cap A\) for any sets \(A\) and \(B\). However, set difference is not commutative. In general, \(A\smallsetminus B \not= B\smallsetminus A\).

Example

Suppose that \(A=\{a,b,c\}\), that \(B=\{b,d\}\), and that \(C=\{d,e,f\}\). Then we can apply the definitions of union, intersection, and set difference to compute, for example, that:

\[\begin{split}\begin{align*} A\cup B &= \{a,b,c,d\} & A\cap B &= \{b\} & A\smallsetminus B &= \{a,c\}\\ A\cup C &= \{a,b,c,d,e,f\}&A\cap C&= \emptyset & A\smallsetminus C &= \{a,b,c\} \end{align*}\end{split}\]

In this example, the sets \(A\) and \(C\) have no elements in common, so that \(A\cap C=\emptyset\). There is a term for this: Two sets are said to be disjoint if they have no elements in common. That is, for any sets \(A\) and \(B\), \(A\) and \(B\) are said to be disjoint if and only if \(A\cap B=\emptyset\).

Of course, the set operations can also be applied to sets that are defined by predicates. The next example illustrates this.

Example

let \(L(x)\) be the predicate ‘\(x\) is lucky’, and let \(W(x)\) be the predicate ‘\(x\) is wise’, where the domain of discourse for each predicate is the set of people. Let \(X = \{x| L(x)\}\), and let \(Y=\{x| W(x)\}\). Then

\[\begin{split}\begin{align*} X\cup Y &= \{x| L(x)\vee W(x)\} = \{\text{people who are lucky or wise}\}\\ X\cap Y &= \{x| L(x)\wedge W(x)\} = \{\text{people who are lucky and wise}\}\\ X\smallsetminus Y &= \{x| L(x)\wedge \lnot W(x)\} = \{\text{people who are lucky but not wise}\}\\ Y\smallsetminus X &= \{x| W(x)\wedge \lnot L(x)\} = \{\text{people who are wise but not lucky}\} \end{align*}\end{split}\]

Warning

You have to be a little careful with the English word ‘and’. We might say that the set \(X\cup Y\) contains people who are lucky and people who are wise. But what this means is that a person gets into the set \(X\cup Y\) either by being lucky or by being wise, so \(X\cup Y\) is defined using the logical ‘or’ operator, \(\vee\).

Table 4.1 Some of the notations that are defined in this section. \(A\) and \(B\) are sets, and \(a\) is an entity.#

Notation

Definition

\(a\in A\)

\(a\) is a member (or element) of \(A\)

\(a\not\in A\)

\(\lnot(a\in A)\), \(a\) is not a member of \(A\)

\(\emptyset\)

the empty set, which contains no elements

\(A\subseteq B\)

\(A\) is a subset of \(B\), \(\forall x(x\in A\rightarrow x\in B)\)

\(A\varsubsetneq B\)

\(A\) is a proper subset of \(B\), \(A\subseteq B \wedge A\not=B\)

\(A\supseteq B\)

\(A\) is a superset of \(B\), same as \(B\subseteq A\)

\(A\varsupsetneq B\)

\(A\) is a proper superset of \(B\), same as \(B\varsubsetneq A\)

\(A=B\)

\(A\) and \(B\) have the same members, \(A\subseteq B\wedge B\subseteq A\)

\(A\cup B\)

union of \(A\) and \(B\), ${x

\(A\cap B\)

intersection of \(A\) and \(B\), ${x

\(A\smallsetminus B\)

set difference of \(A\) and \(B\), ${x

\(A\Delta B\)

symmetric difference of \(A\) and \(B\), ${x

\(\mathscr{P}(A)\)

power set of \(A\), ${X

4.1.4. Visualising sets[1]#

It can be helpful to visualise sets. A Venn diagram shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. So a Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set. The points inside a curve (circle) labelled \(S\) represent elements of the set \(S\), while points outside the boundary represent elements not in the set \(S\). Fig. 4.1 shows our example set which opened the section.

Venn diagrams help us to visualise sets and set operations. For example, the set of all elements that are members of both sets \(S\) and \(T\), \(S\cap T\), is represented visually by the area of overlap of the regions \(S\) and \(T\): see Fig. 4.2. In Venn diagrams the curves are overlapped in every possible way, showing all possible relations between the sets. You can find it useful to draw a Venn diagram to gain intuition of what’s happening. On their own, however, Venn diagrams do not offer a proof for theorems in set theory.

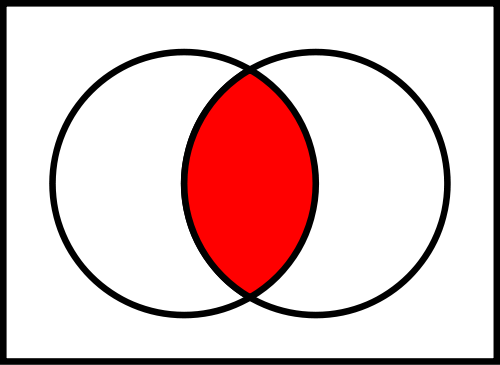
../../_images/venn-intersection.png

Fig. 4.2 Venn diagram of the intersection of two sets.#

4.1.5. Sets of sets#

Sets can contain other sets as elements. For example, the notation \(\{a,\{b\}\}\) defines a set that contains two elements, the entity \(a\) and the set \(\{b\}\). Since the set \(\{b\}\) is a member of the set \(\{a,\{b\}\}\), we have that \(\{b\}\in\{a,\{b\}\}\). On the other hand, provided that \(a\not=b\), the statement \(\{b\}\subseteq\{a,\{b\}\}\) is false, since saying \(\{b\}\subseteq\{a,\{b\}\}\) is equivalent to saying that \(b\in\{a,\{b\}\}\), and the entity \(b\) is not one of the two members of \(\{a,\{b\}\}\). For the entity \(a\), it is true that \(\{a\}\subseteq\{a,\{b\}\}\) and for the set \(\{b\}\), it is true that \(\{\{b\}\} \subseteq \{a,\{b\}\}\). Study these examples carefully before you continue, as many students struggle with the notion and notation of putting sets in sets.

Given a set \(A\), we can construct the set that contains all the subsets of \(A\). This set is called the power set of \(A\), and is denoted \(\mathscr{P}(A)\). Formally, we define

\[\mathscr{P}(A)=\{X| X\subseteq A\}.\]

Example

For example, if \(A=\{a,b\}\), then the subsets of \(A\) are the empty set, \(\{a\}\), \(\{b\}\), and \(\{a,b\}\), so the power set of \(A\) is set given by

\[\mathscr{P}(A) = \{\,\emptyset,\,\{a\},\,\{b\},\,\{a,b\}\,\}.\]

So the power set of of \(A\) has four elements. Does this surprise you?

Note that since the empty set is a subset of any set, the empty set is an element of the power set of any set. That is, for any set \(A\), \(\emptyset\subseteq A\) and \(\emptyset\in\mathscr{P}(A)\). Since the empty set is a subset of itself, and is its only subset, we have that \(\mathscr{P}(\emptyset) = \{\emptyset\}\). The set \(\{\emptyset\}\) is not empty. It contains one element, namely \(\emptyset\).

Person

../../_images/russell.png

The Nobel Prize was won by Bertrand Russell (1872–1970), a dominant figure in British thought during the twentieth century. Russell was a philosopher and mathematician, and also a historian, social critic and political activist. With A. N. Whitehead, Russell wrote Principia Mathematica, an epic attempt to create a logical basis for mathematics. His work has had a considerable influence on computer science, and not just for his contributions to logic and set theory: he proposed the beginnings of what are now called type systems.

Source: en.wikipedia.org/wiki/Bertrand_Russell.

We remarked earlier in this section that the notation \(\{x | P(x)\}\) is only valid if the domain of discourse of \(P\) is a set. This might seem a rather puzzling thing to say—after all, why and how would the domain of discourse be anything else? The answer is related to Russell’s Paradox, which we mentioned briefly in Section 3 and which shows that it is logically impossible for the set of all sets to exist. This impossibility can be demonstrated using a proof by contradiction. In the proof, we use the existence of the set of all sets to define another set which cannot exist because its existence would lead to a logical contradiction.

Theorem 4.2

There is no set of all sets.

Proof. Suppose that the set of all sets exists. We will show that this assumption leads to a contradiction. Let \(V\) be the set of all sets. We can then define the set \(R\) to be the set which contains every set that does not contain itself. That is,

\[R=\{X\in V| X\not\in X\}\]

Now, we must have either \(R\in R\) or \(R\not\in R\). We will show that either case leads to a contradiction.

Consider the case where \(R\in R\). Since \(R\in R\), \(R\) must satisfy the condition for membership in \(R\). A set \(X\) is in \(R\) iff \(X\not\in X\). To say that \(R\) satisfies this condition means that \(R\not\in R\). That is, from the fact that \(R\in R\), we deduce the contradiction that \(R\not\in R\).

Now consider the remaining case, where \(R\not\in R\). Since \(R\not\in R\), \(R\) does not satisfy the condition for membership in \(R\). Since the condition for membership is that \(R\not\in R\), and this condition is false, the statement \(R\not\in R\) must be false. But this means that the statement \(R\in R\) is true. From the fact that \(R\not\in R\), we deduce the contradiction that \(R\in R\).

Since both possible cases, \(R\in R\) and \(R\not\in R\), lead to contradictions, we see that it is not possible for \(R\) to exist. Since the existence of \(R\) follows from the existence of \(V\), we see that \(V\) also cannot exist.

□

Tip

This (in)famous contradiction has been adapted to natural language to make it easier to convey the problem to laymen. Unfortunately many of these translations are flawed. Can you think of a solution for the following for instance? ‘’The barber of Seville shaves all men who do not shave themselves. Who shaves the barber?’’

To avoid Russell’s paradox, we must put limitations on the construction of new sets. We can’t force the set of all sets into existence simply by thinking of it. We can’t form the set \(\{x| P(x)\}\) unless the domain of discourse of \(P\) is a set. Any predicate \(Q\) can be used to form a set \(\{x\in X| Q(x)\}\), but this notation requires a pre-existing set \(X\). Predicates can be used to form subsets of existing sets, but they can’t be used to form new sets completely from scratch.

The notation \(\{x\in A| P(x)\}\) is a convenient way to effectively limit the domain of discourse of a predicate, \(P\), to members of a set, \(A\), that we are actually interested in. We will use a similar notation with the quantifiers \(\forall\) and \(\exists\). The proposition \((\forall x\in A)(P(x))\) is true if and only if \(P(a)\) is true for every element \(a\) of the set \(A\). And the proposition \((\exists x\in A)(P(x))\) is true if and only if there is some element \(a\) of the set \(A\) for which \(P(a)\) is true. These notations are valid only when \(A\) is contained in the domain of discourse for \(P\). As usual, we can leave out parentheses when doing so introduces no ambiguity. So, for example, we might write \(\forall x\in A\;P(x)\).

4.1.6. Ordered collections: Tuples#

If \(a\) and \(b\) are entities, then \((a,b)\) denotes the ordered pair containing \(a\) and \(b\). The ordered pair \((a,b)\) differs from the set \(\{a,b\}\) because a set is not ordered. That is, \(\{a,b\}\) and \(\{b,a\}\) denote the same set, but if \(a\not=b\), then \((a,b)\) and \((b,a)\) are different ordered pairs. More generally, two ordered pairs \((a,b)\) and \((c,d)\) are equal if and only if both \(a=c\) and \(b=d\). If \((a,b)\) is an ordered pair, then \(a\) and \(b\) are referred to as the coordinates of the ordered pair. In particular, \(a\) is the first coordinate and \(b\) is the second coordinate.

Tip

In high school you would also have to write (x,y)-coordinates using this ordered pair notation. For instance you would say that the line \(y = ax + b\) intersects the y-axis at \((0,b)\) and the x-axis at \((-\dfrac{b}{a},0)\).

You can extend this concept to more than just pairs. With three elements we can create ordered triples \((a,b,c)\).
The definition for four or more coordinates is similar.
The general term for such an ordered collection is tuple (recall this section) or, more specifically, ordered n-tuple.
For example, \((a,b,c,d,e)\) is an ordered 5-tuple.

4.1.7. One more set operation: Cartesian product#

If \(A\) and \(B\) are sets, then we can form the set \(A\times B\) which is defined by \(A\times B= \{(a,b)| a\in A \text{ and } b\in B\}.\) This set is called the cross product or Cartesian product of the sets \(A\) and \(B\). The set \(A\times B\) contains every ordered pair whose first coordinate is an element of \(A\) and whose second coordinate is an element of \(B\). For example, if \(X=\{c,d\}\) and \(Y=\{1,2,3\}\), then \(X\times Y=\{(c,1), (c,2), (c,3),\) \((d,1),(d,2), (d,3)\}\).

It is possible to extend this idea to the cross product of more than two sets. The cross product of the three sets \(A\), \(B\), and \(C\) is denoted \(A\times B\times C\) and produced ordered triples \((a,b,c)\) where \(a \in A, b \in B, c\in C\). Another example can be found in the homework duos you have formed for this course. Each of these pairs of students is a 2-tuple, from the set \(S \times S\) where \(S\) is the set of students currently taking Reasoning & Logic.

4.1.8. Mathematical induction revisited#

We end this section by returning to the topic of mathematical induction. First, we will give proofs of the two forms of the principle of mathematical induction. These proofs were omitted from the previous chapter, but only for the lack of a bit of set notation. In fact, the principle of mathematical induction is valid only because it follows from one of the basic axioms that define the natural numbers, namely the fact that any non-empty set of natural numbers has a smallest element. Given this axiom, we can use it to prove the following two theorems:

Theorem 4.3

Let \(P\) be a one-place predicate whose domain of discourse includes the natural numbers. Suppose that \(P(0)\wedge \big(\forall k\in\mathbb{N}\;(P(k)\rightarrow P(k+1))\big)\). Then \(\forall n\in\mathbb{N},\,P(n)\).

Proof. Suppose that both \(P(0)\) and \(\big(\forall k\in\mathbb{N}\,(P(k)\rightarrow P(k+1))\big)\) are true, but that \(\big(\forall n\in\mathbb{N},\,P(n)\big)\) is false. We show that this assumption leads to a contradiction.

Since the statement \(\forall n\in\mathbb{N},\,P(n)\) is false, its negation, \(\lnot(\forall n\in\mathbb{N},\,P(n))\), is true. The negation is equivalent to \(\exists n\in\mathbb{N},\,\lnot P(n)\). Let \(X=\{n\in\mathbb{N}| \lnot P(n)\}\). Since \(\exists n\in\mathbb{N},\,\lnot P(n)\) is true, we know that \(X\) is not empty. Since \(X\) is a non-empty set of natural numbers, it has a smallest element. Let \(x\) be the smallest element of \(X\). That is, \(x\) is the smallest natural number such that \(P(x)\) is false. Since we know that \(P(0)\) is true, \(x\) cannot be 0. Let \(y=x-1\). Since \(x\not=0\), \(y\) is a natural number. Since \(y<x\), we know, by the definition of \(x\), that \(P(y)\) is true. We also know that \(\forall k\in\mathbb{N}\,(P(k)\rightarrow P(k+1))\) is true. In particular, taking \(k=y\), we know that \(P(y)\rightarrow P(y+1)\). Since \(P(y)\) and \(P(y)\rightarrow P(y+1)\), we deduce by modus ponens that \(P(y+1)\) is true. But \(y+1=x\), so we have deduced that \(P(x)\) is true. This contradicts the fact that \(P(x)\) is false. This contradiction proves the theorem.

□

Theorem 4.4

Let \(P\) be a one-place predicate whose domain of discourse includes the natural numbers. Suppose that \(P(0)\) is true and that

\[(P(0)\wedge P(1)\wedge\cdots\wedge P(k))\rightarrow P(k+1)\]

is true for each natural number \(k\geq 0\).
Then it is true that \(\forall n\in\mathbb{N},\,P(n)\).

Proof. Suppose that \(P\) is a predicate that satisfies the hypotheses of the theorem, and suppose that the statement \(\forall n\in\mathbb{N},\,P(n)\) is false. We show that this assumption leads to a contradiction.

Let \(X=\{n\in\mathbb{N}| \lnot P(n)\}\). Because of the assumption that \(\forall n\in\mathbb{N},\,P(n)\) is false, \(X\) is non-empty. It follows that \(X\) has a smallest element. Let \(x\) be the smallest element of \(X\). The assumption that \(P(0)\) is true means that \(0\not\in X\), so we must have \(x>0\). Since \(x\) is the smallest natural number for which \(P(x)\) is false, we know that \(P(0)\), \(P(1)\), … , and \(P(x-1)\) are all true. From this and the fact that \((P(0)\wedge P(1)\wedge\cdots\wedge P(x-1))\rightarrow P(x)\), we deduce that \(P(x)\) is true. But this contradicts the fact that \(P(x)\) is false. This contradiction proves the theorem.

□

4.1.9. Structural induction#

Next, while we are on the topic of induction, let’s generalise the idea of induction to also apply it to sets. This more general form of induction is often called structural induction. Structural induction is used to prove that some proposition \(P(x)\) holds for all \(x\) of some sort of recursively defined structure, such as formulae, lists, or trees—or recursively-defined sets. In a proof by structural induction we show that the proposition holds for all the ‘minimal’ structures, and that if it holds for the immediate substructures of a certain structure \(S\), then it must hold for \(S\) also. Structural induction is useful for proving properties about algorithms; sometimes it is used together with invariants for this purpose.

To get an idea of what a ‘recursively defined set’ might look like, consider the following definition of the set of natural numbers \(\mathbb{N}\).

Basis:

\(0 \in \mathbb{N}\).

Succession:

\(x \in \mathbb{N} \rightarrow x+1 \in \mathbb{N}\).

Exclusivity:

No other elements other than those outlined by the rules above are in \(\mathbb{N}\).

This definition is similar to one we have seen before, first stating that \(0 \in \mathbb{N}\) and then saying that we can add \(1\) to an element in \(\mathbb{N}\) to get another element of \(\mathbb{N}\). The final clause is needed to ensure that other items are not part of \(\mathbb{N}\). Without it, you and I, as well as \(\pi\), ‘New York City’, and ‘King Willem-Alexander’ might have been in the set. After all there was no reason for those elements not to be in there.

Now compare that recursive definition, with the method for mathematical induction we have seen before:

Base case:

Prove that \(P(0)\) holds.

Inductive case:

Prove that \(\forall k \in\mathbb{N} (P(k) \rightarrow P(k+1))\) holds.

Conclusion:

\(\forall n \in\mathbb{N} (P(n))\) holds.

As we can see mathematical induction and this recursive definition show large similarities. The base case of the induction proves the property for the basis of our recursive definition and the inductive step proves the property for the succession rule. In fact, this similarity is no coincidence and we can generalise this method to get to structural induction.

Consider for instance the set \(\mathit{PROP}\), which represents all valid formulae in propositional logic:

Atoms:

\(p_i \in \mathit{PROP}\) for all \(i \in \mathbb{N}\).

Negation:

\(x \in \mathit{PROP} \rightarrow \lnot x \in PROP\).

Binary connective:

\(x,y\in \mathit{PROP} \rightarrow (x * y) \in \mathit{PROP}\), s.t.\ \(* \in \{\wedge,\vee,\rightarrow,\leftrightarrow\}\).

Exclusivity:

Nothing else is in \(\mathit{PROP}\).

Using this definition of the set \(\mathit{PROP}\) we can use structural induction to prove certain claims about \(\mathit{PROP}\). For instance we can prove that every formula in \(\mathit{PROP}\) has equally many left parentheses ‘(’ and right parentheses ‘)’.

Proof. Let \(l(\phi)\) denote the number of left parentheses in a formula \(\phi\). Similarly let \(r(\phi)\) denote the number of right parentheses. Let \(P(\phi)\) be the statement that \(l(\phi) = r(\phi)\). We need to prove that \(\forall \phi \in \mathit{PROP} (P(\phi))\).

Base case: Consider the Atoms rule of the definition of \(\mathit{\mathit{PROP}}\): \(l(p_i) = 0 = r(p_i)\). Therefore \(P(p_i)\) holds.

Inductive case: We want to show that if the statement is true for \(x,y \in \mathit{PROP}\) (where \(x\) and \(y\) are arbitrary formula), then it is true for \(\lnot x\) and \((x * y)\) for all \(* \in \{\vee,\wedge,\rightarrow,\leftrightarrow\}\). That is, we must prove the implication \((P(x) \wedge P(y)) \rightarrow (P(\lnot x) \wedge P((x * y)))\). So we assume \(P(x) \wedge P(y)\), that is, we assume that for both formula \(x\) and \(y\): \(l(x) = r(x)\) and \(l(y) = r(y)\). We want to prove \(P(\lnot x)\), that is, that for \(\lnot x\) \(l(\lnot x) = r(\lnot x)\)

\[\begin{split}\begin{align*} l(\lnot x) &= l(x) & \text{by the Negation rule of $\mathit{PROP}$}\\ &= r(x) & \text{by the inductive hypothesis}\\ &= r(\lnot x) & \text{by the Negation rule of $\mathit{PROP}$} \end{align*}\end{split}\]

Secondly we prove that \(P((x * y))\) holds for all \(* \in \{\vee, \wedge, \rightarrow, \leftrightarrow\}\):

\[\begin{split}\begin{align*} l((x * y)) &= 1 + l(x) + l(y) & \text{by the Binary connective rule of $\mathit{PROP}$}\\ &= 1 + r(x) + r(y) & \text{by the inductive hypothesis}\\ &= r((x * y)) & \text{by the Binary connective rule of $\mathit{PROP}$} \end{align*}\end{split}\]

Altogether, we have shown that \(P(p_i)\) holds and that, for all \(x,y \in \mathit{PROP}\) and \(* \in \{\vee,\wedge,\rightarrow,\leftrightarrow\}\), \((P(x) \wedge P(y)) \to (P(\lnot x) \wedge P((x * y))\) is true. Therefore, by the principle of structural induction, \(P(\phi)\) is true for all \(\phi \in \mathit{PROP}\), so for all propositional formula the number of left parentheses equals the number of right parentheses. This completes the proof by structural induction.

□

Such structural induction proofs can be applied on any recursively defined set of numbers, formulae or even strings (pieces of text) or lists or trees, making this a powerful generalised proof method.

Video

In one of the pencasts of this course, we show an example of applying structural induction over a recursively defined set of strings: https://youtu.be/HAtgYJbCMf0

4.1.10. Revisiting trees#

In Section 3.8 we defined trees very informally. Now that we know about tuples and recursive sets, we can formally define the set of trees \(\mathit{TREE}\) as follows:

Empty Tree

\(\emptyset \in \mathit{TREE}\)

Leaf Nodes

\((x, \emptyset) \in \mathit{TREE}\) if \(x \in D\)

Internal Nodes

\((x, (T_1, T_2, ... , T_k)) \in \mathit{TREE}\) if \(x \in D \,\wedge\, \forall i (1 \leq i \leq k \to T_i \in \mathit{TREE})\) for some integer \(k\)

Exclusivity

Nothing else is in \(\mathit{TREE}\)

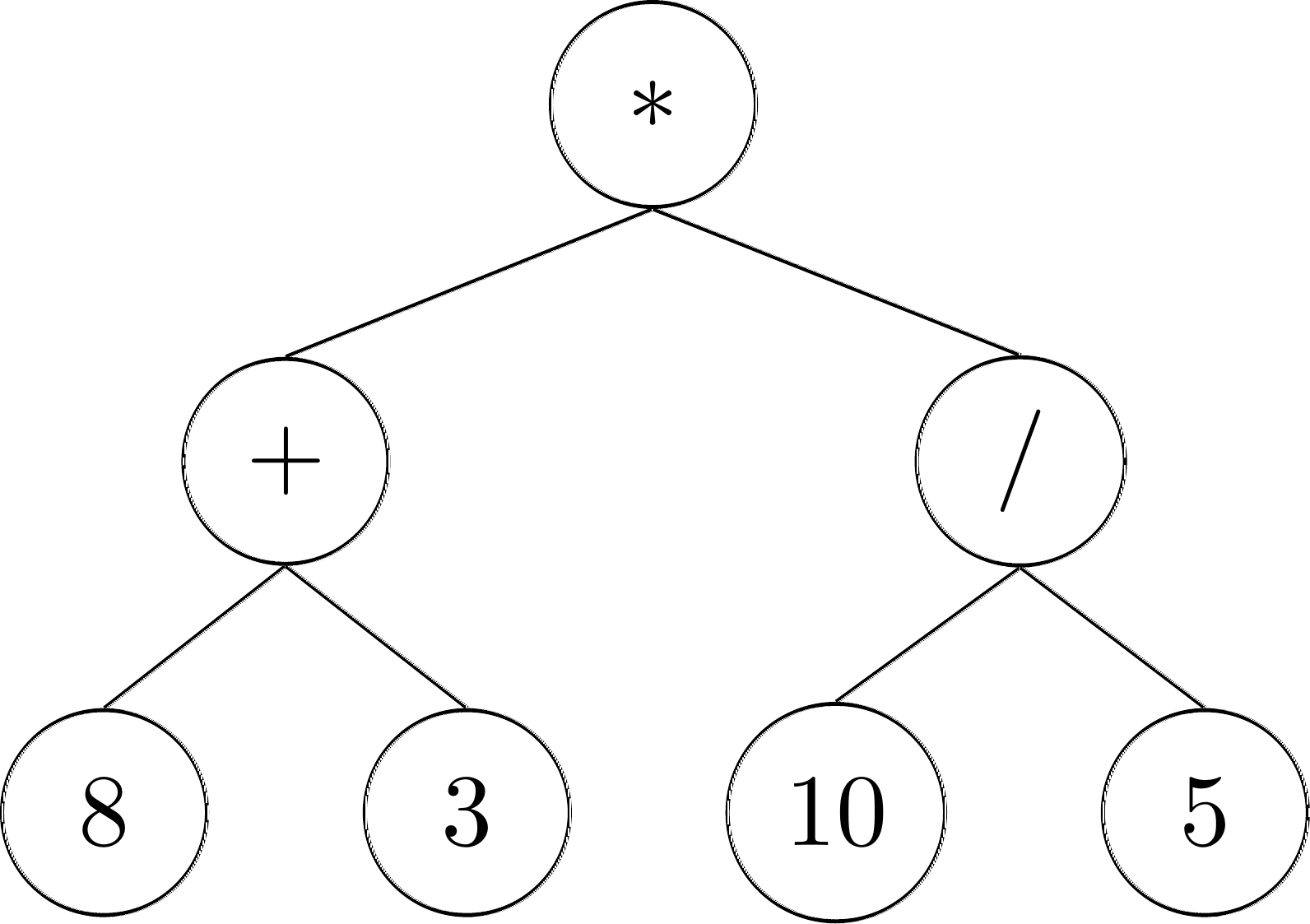
Note that in this definition we have included a free variable \(D\). This is the domain of values that are allowed in the tree. For example for our parse trees from Section 3.8.2 we could use \(D = \mathbb{R} \cup \{+,-,/,*\}\).[2]

This way we can have the following tree be formally represented as:

\( (*, ((+,((8,\emptyset),(3,\emptyset))),(/,((10,\emptyset),(5,\emptyset))))) \)

You can probably see now why we often choose to represent trees visually!

../../_images/tikz_6.png

Note that we could alternatively have represented our leaf node \(8\) as \((8, (\emptyset))\). After all, one could argue this also describe a node without any children containing values. However, this description describes a different tree. After all it now says that the node \(8\) has a child (and thus is an internal node), but that this child has no value (it is an empty tree). To visualise this, other authors sometimes use squares as such:

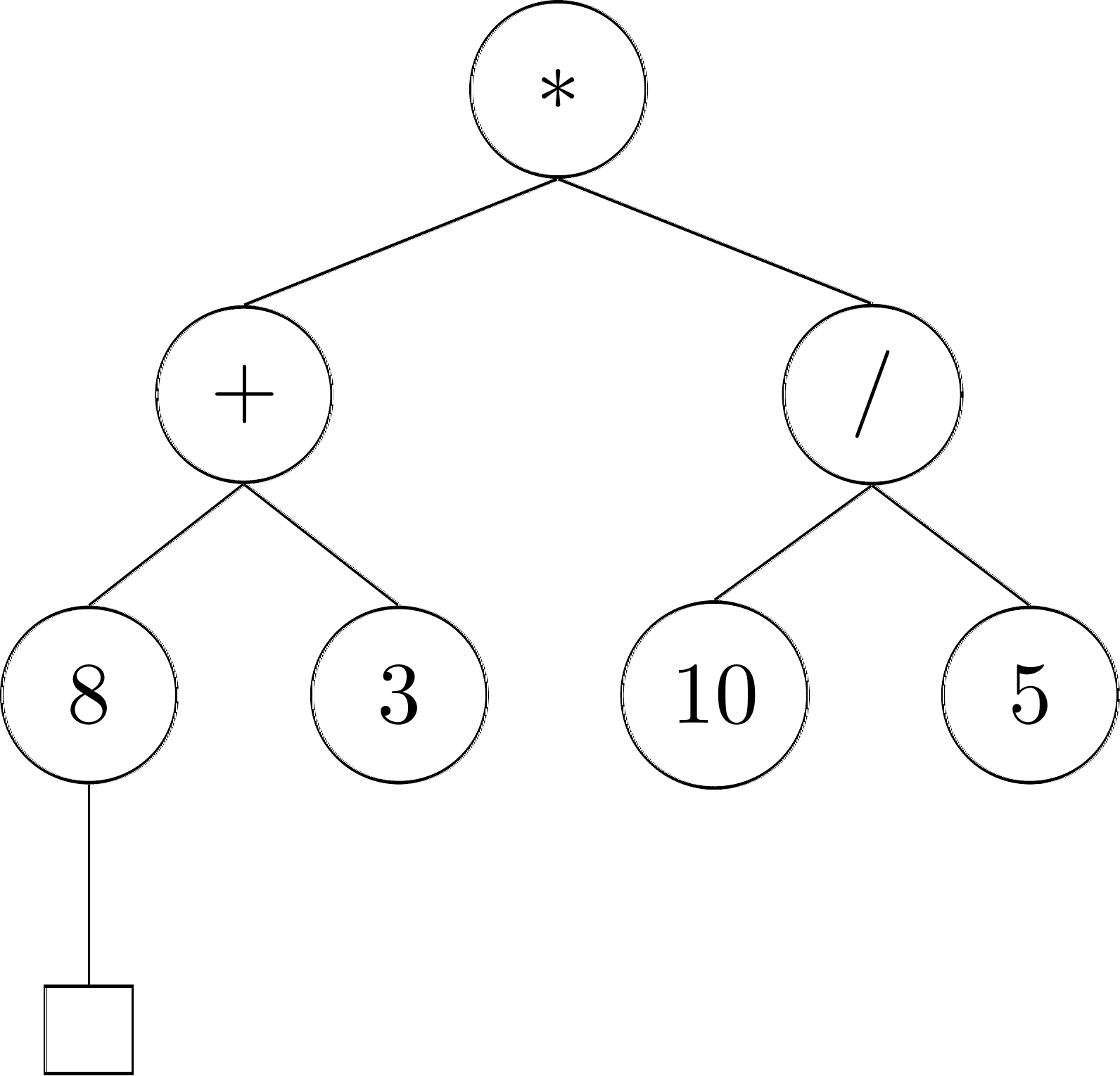
../../_images/tikz_7.png

Notice also how we can now ‘easily’ define binary trees by simply limiting \(k = 2\) in the Internal Nodes rule. For example \((8, ((3, (\emptyset, (2, \emptyset))), \emptyset))\) would be a binary tree, represented like this:

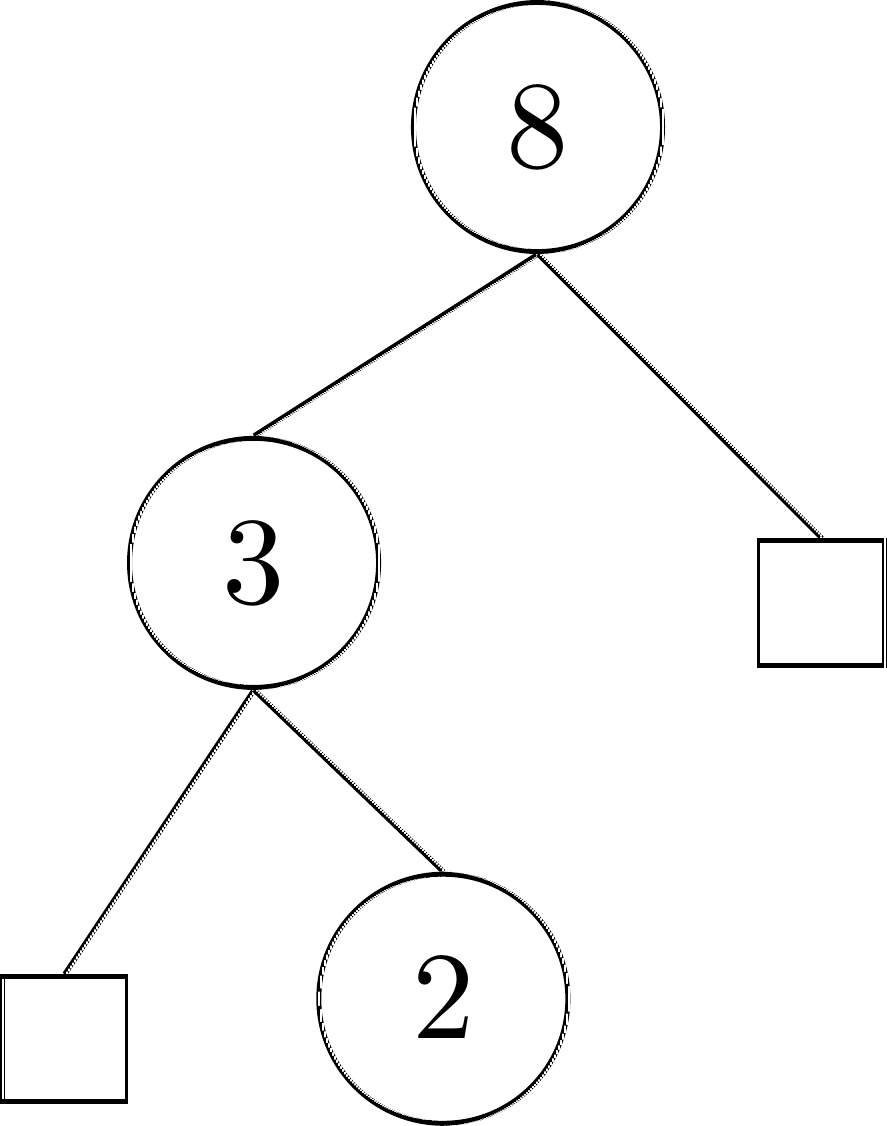
../../_images/tikz_8.png

But have you spotted an unfortunate side effect of this definition? In our visualisation, both our squares and our node containing \(2\) are considered leaves. After all they have no children! As a result, some books instead use the following definition for binary trees. This removes the ambiguity on the definition of a leaf, but as a downside does not allow any leaf to have a value. It is a nice example of one of the many trade-offs in computer science.

Leaf Nodes

\(\emptyset \in \mathit{BTREE}\)

Internal Nodes

\((x, (T_1, T_2)) \in \mathit{BTREE}\) if \(x \in D \wedge T_1, T_2 \in \mathit{BTREE}\)

Exclusivity

Nothing else is in \(\mathit{BTREE}\)

Now that we have formalised our definition of binary trees, we can also start proving interesting properties about them. One such property is that the number of leaves of a binary tree \(n_L \leq 2^h\) where \(h\) is the height of the tree. A proof for this claim can now follow our structural induction format as outlined in the previous section:

Proof. Base case (Empty Tree): consider the Empty Tree rule of the definition of \(\mathit{TREE}\). The empty tree has no nodes, so a height of 0 and also no leaves. Hence \(n_L = 0 \leq 2^{0} = 1\) holds.

Base case (Leaf Nodes): consider the Leaf Nodes rule of the definition of \(\mathit{TREE}\). A leaf node has a height of 0 as longest path from a leaf to the root excluding the leaf has no nodes (there are no nodes except the leaf!), hence \(n_L = 1 \leq 2^0 = 1\) holds.

Inductive case (Internal Nodes): Let \(T_1\) and \(T_2\) be some trees with \(n_{L_1}\) and \(n_{L_2}\) as their number of leaves and \(h_1\) and \(h_2\) as their heights respectively. Now assume that \(n_{L_1} \leq 2^{h_1}\) and \(n_{L_2} \leq {2^h_2}\) (IH). Now we use the Internal Nodes rule to create a new Tree \(T = (x, (T_1, T_2))\) for some value \(x\). For this tree \(T\), \(n_L = n_{L_1} + n_{L_2}\) and the height \(h = \max(h_1, h_2)+1\). Now we use a division into cases:

  • \(h_1 > h_2\) In this case it follows that \(n_{L_2} \leq 2^{h_2} < 2^{h_1}\). As a result: \(n_L = n_{L_1} + n_{L_2} < 2\cdot 2^{h_1} = 2^{h_1+1} = 2^{\max(h_1, h_2) +1}\).

  • \(h_1 = h_2\) In this case it follows that \(n_{L_2} \leq 2^{h_2} = 2^{h_1}\). As a result: \(n_L = n_{L_1} + n_{L_2} \leq 2\cdot 2^{h_1} = 2^{h_1+1} = 2^{\max(h_1, h_2) +1}\).

  • \(h_1 < h_2\) Is analogous to the first case.

Now we have shown that the property holds for all rules of \(\mathit{TREE}\) where \(k = 2\) in the internal nodes rule. This completes the proof by structural induction.

□

4.1.11. Exercises#