2.3. Application: Logic Circuits#

As we saw in Section 1, computers have a reputation—not always deserved—for being ‘logical’. But fundamentally, deep down, they are made of logic in a very real sense. The building blocks of computers are logic gates, which are electronic components that compute the values of simple propositions such as \(p\wedge q\) and \(\lnot p\). (Each gate is in turn built of even smaller electronic components called transistors, but this needn’t concern us here: see the course Computer Organisation.)

Note

Don’t worry, logic circuits will be examined in Computer Organisation, not in Reasoning & Logic. They are a good example and application of propositional logic, and that’s why we’re talking about them in this section. Normal forms (Section 2.3.4) are definitely on the syllabus, however, so pay attention!

2.3.1. Logic gates*#

A wire in a computer can be in one of two states, which we can think of as being on and off. These two states can be naturally associated with the Boolean values \(\mathbb{T}\) and \(\mathbb{F}\). When a computer computes, the multitude of wires inside it are turned on and off in patterns that are determined by certain rules. The rules involved can be most naturally expressed in terms of logic. A simple rule might be: ‘’turn wire \(C\) on whenever wire \(A\) is on and wire \(B\) is on’’. This rule can be implemented in hardware as an AND gate. An and gate is an electronic component with two input wires and one output wire, whose job is to turn its output on when both of its inputs are on and to turn its output off in any other case. If we associate ‘on’ with \(\mathbb{T}\) and ‘off’ with \(\mathbb{F}\), and if we give the names \(A\) and \(B\) to the inputs of the gate, then the gate computes the value of the logical expression \(A\wedge B\). In effect, \(A\) is a proposition with the meaning ‘’the first input is on’’, and \(B\) is a proposition with the meaning ‘’the second input is on’’. The and gate functions to ensure that the output is described by the proposition \(A \wedge B\). That is, the output is on if and only if the first input is on and the second input is on.

As you hopefully know from Computer Organisation, an OR gate is an electronic component with two inputs and one output which turns its output on if either (or both) of its inputs is on. If the inputs are given names \(A\) and \(B\), then the or gate computes the logical value of \(A\vee B\). A NOT gate has one input and one output, and it turns its output off when the input is on and on when the input is off. If the input is named \(A\), then the not gate computes the value of \(\lnot A\).

Warning

As we mentioned earlier, other textbooks might use different notations to represent a negation. For instance a bar over the variable \(\bar{x}\) or a \(\sim\) symbol. In digital logic (and thus in your Computer Organisation course) you will also often find the \(+\) symbol to represent an ‘or’ and a \(\cdot\) (dot) symbol to represent an ‘and’.

Other types of logic gates are, of course, possible. Gates could be made to compute \(A\rightarrow B\) or \(A\oplus B\), for example. However, any computation that can be performed by logic gates can be done using only and, or, and not gates, as we will see below. (In practice, however, nand gates and nor gates, which compute the values of \(\lnot(A\wedge B)\) and \(\lnot(A\vee B)\) respectively, are often used because they are easier to build from transistors than and and or gates.)

2.3.2. Combining gates to create circuits*#

The three types of logic gates are represented by standard symbols, as shown in Fig. 2.1. Since the inputs and outputs of logic gates are just wires carrying on/off signals, logic gates can be wired together by connecting outputs from some gates to inputs of other gates. The result is a logic circuit. An example is also shown in Fig. 2.1.

../../_images/fig1-3.png

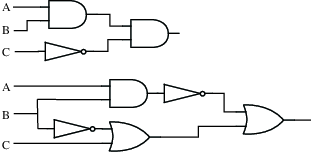
Fig. 2.1 The standard symbols for the three basic logic gates, and a logic circuit that computes the value of the logical expression \((\lnot A)\wedge(B\vee\lnot(A\wedge C))\). The input wires to each logic gate are on the left, with the output wire on the right. Note that when wires cross each other in a diagram such as this, the wires don’t actually intersect unless there is a black circle at the point where they cross.#

The logic circuit in the figure has three inputs, labeled \(A\), \(B\), and \(C\). The circuit computes the value of the compound proposition \((\lnot A)\wedge(B\vee\lnot(A\wedge C))\). That is, when \(A\) represents the proposition ‘’the input wire labeled \(A\) is on,’’ and similarly for \(B\) and \(C\), then the output of the circuit is on if and only if the value of the compound proposition \((\lnot A)\wedge(B\vee\lnot(A\wedge C))\) is true.

Given any compound proposition made from the operators \(\wedge\), \(\vee\), and \(\lnot\), it is possible to build a logic circuit that computes the value of that proposition. The proposition itself is a blueprint for the circuit. As noted in Section 2.1, every logical operator that we have encountered can be expressed in terms of \(\wedge\), \(\vee\), and \(\lnot\), so in fact every compound proposition that we know how to write can be computed by a logic circuit.

Given a proposition constructed from \(\wedge\), \(\vee\), and \(\lnot\) operators, it is easy to build a circuit to compute it. First, identify the main operator in the proposition—the one whose value will be computed last. Consider \((A\vee B)\wedge\lnot(A\wedge B)\). This circuit has two input values, \(A\) and \(B\), which are represented by wires coming into the circuit. The circuit has an output wire that represents the computed value of the proposition. The main operator in \((A\vee B)\wedge\lnot(A\wedge B)\), is the first \(\wedge\), which computes the value of the expression as a whole by combining the values of the subexpressions \(A\vee B\) and \(\lnot(A\wedge B)\). This \(\wedge\) operator corresponds to an and gate in the circuit that computes the final output of the circuit.

Once the main operator has been identified and represented as a logic gate, you just have to build circuits to compute the input or inputs to that operator. In the example, the inputs to the main and gate come from two subcircuits. One subcircuit computes the value of \(A\vee B\) and the other computes the value of \(\lnot(A\wedge B)\). Building each subcircuit is a separate problem, but smaller than the problem you started with. Eventually, you’ll come to a gate whose input comes directly from one of the input wires—\(A\) or \(B\) in this case—instead of from a subcircuit.

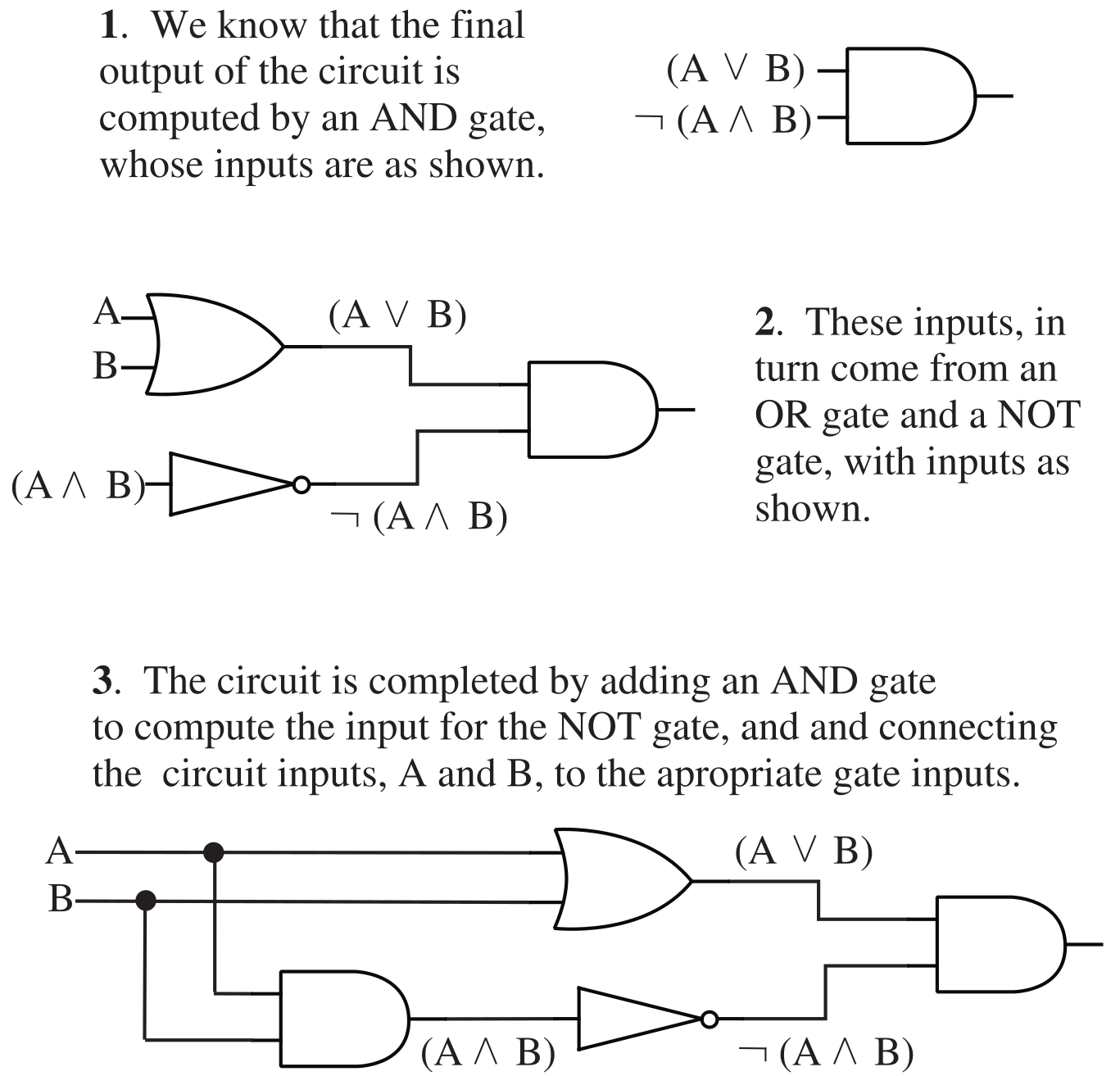
../../_images/fig-1-4.png

Fig. 2.2 Stages in the construction of a circuit that computes the compound proposition \((A\vee B)\wedge\lnot(A\wedge B)\).#

2.3.3. From circuits to propositions*#

So, every compound proposition is computed by a logic circuit with one output wire. Is the reverse true? That is, given a logic circuit with one output, is there a proposition that expresses the value of the output in terms of the values of the inputs? Not quite. When you wire together some logic gates to make a circuit, there is nothing to stop you from introducing feedback loops. A feedback loop occurs when the output from a gate is connected—possibly through one or more intermediate gates—back to an input of the same gate. Fig. 2.3 shows an example of a circuit with a feedback loop. Feedback loops cannot be described by compound propositions, basically because there is no place to start, no input to associate with a propositional variable. But feedback loops are the only thing that can go wrong. A logic circuit that does not contain any feedback loops is called a combinatorial logic circuit. Every combinatorial logic circuit with just one output computes the value of some compound proposition. The propositional variables in the compound proposition are just names associated with the input wires of the circuit. (Of course, if the circuit has more than one output, you can simply use a different proposition for each output.)

../../_images/fig1-5.png

Fig. 2.3 This circuit contains a feedback loop, so it is not a combinatorial logic circuit. The feedback loop includes the and gate and the or gate on the right. This circuit does not compute the value of a compound proposition. This circuit does, however, play an important role in computer memories, since it can be used to store a logical value.#

The key to understanding why this is true is to note that each wire in the circuit—not just the final output wire—represents the value of some proposition.
Furthermore, once you know which proposition is represented by each input wire to a gate, it’s obvious what proposition is represented by the output: You just combine the input propositions with the appropriate \(\wedge\), \(\vee\), or \(\lnot\) operator, depending on what type of gate it is. To find the proposition associated with the final output, you just have to start from the inputs and move through the circuit, labeling the output wire of each gate with the proposition that it represents. 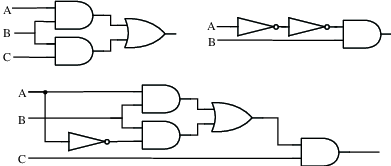Fig. 2.4 illustrates this process.

../../_images/fig1-6.png

Fig. 2.4 Finding the proposition whose value is computed by a combinatorial logic circuit. Each wire in the circuit is labeled with the proposition that it represents. The numbering of the labels shows one of the orders in which they can be associated with the wires. The circuit as a whole computes the value of \(\lnot(A\wedge B)\wedge(B\vee\lnot C)\).#

2.3.4. Disjunctive Normal Form#

Compound propositions, then, correspond naturally with combinatorial logic circuits. But we have still not quite settled the question of just how powerful these circuits and propositions are. We’ve looked at a number of logical operators and noted that they can all be expressed in terms of \(\wedge\), \(\vee\), and \(\lnot\). But might there be other operators that cannot be so expressed? Equivalently, might there be other types of logic gates—possibly with some large number of inputs—whose computations cannot be duplicated with and, or, and not gates? Any logical operator or logic gate computes a value for each possible combination of logical values of its inputs. We could always make a truth table showing the output for each possible combination of inputs. As it turns out, given any such truth table, it is possible to find a proposition, containing only the \(\wedge\), \(\vee\), and \(\lnot\) operators, whose value for each combination of inputs is given precisely by that table.

To see why this is true, it is useful to introduce a particular type of compound proposition. Define a simple term to be either a propositional variable or the negation of a propositional variable. A conjunction of simple terms would then consist of one or more simple terms put together with \(\wedge\) operators. (A ‘conjunction of one simple term’ is just a single simple term by itself. This might not make grammatical sense, but it’s the way mathematicians think.) Some examples of conjunctions of simple terms would be \(p\wedge q\), \(p\), \(\lnot q\), and \(p\wedge\lnot r\wedge \lnot w\wedge s\wedge t\). Finally, we can take one or more such conjunctions and join them into a ‘disjunction of conjunctions of simple terms’. This is the type of compound proposition we need. We can avoid some redundancy by assuming that no propositional variable occurs more than once in a single conjunction (since \(p\wedge p\) can be replaced by \(p\), and if \(p\) and \(\lnot p\) both occur in a conjunction, then the value of the conjuction is false, and it can be eliminated.) We can also assume that the same conjunction does not occur twice in the disjunction.

Warning

Normal forms are part of the syllabus for Reasoning & Logic. These normal forms, such as Disjunctive Normal Form (this subsection) and Conjunctive Normal Form (see the exercises), are important in propositional logic. There are normal forms for other logics, too, such as for predicate logic which we’ll look at in the next Section 2.4.

Definition 2.6

A compound proposition is said to be in disjunctive normal form, or DNF, if it is a disjunction of conjunctions of simple terms, and if, furthermore, each propositional variable occurs at most once in each conjunction and each conjunction occurs at most once in the disjunction.

Using \(p\), \(q\), \(r\), \(s\), \(A\), and \(B\) as propositional variables, here are a few examples of propositions that are in disjunctive normal form:

\[\begin{split}\begin{array}{c} (p\wedge q\wedge r)\vee(p\wedge\lnot q\wedge r\wedge s)\vee(\lnot p\wedge\lnot q)\\ (p\wedge \lnot q)\\ (A\wedge \lnot B)\vee(\lnot A\wedge B)\\ p\vee(\lnot p\wedge q)\vee(\lnot p\wedge\lnot q\wedge r)\vee(\lnot p\wedge\lnot q\wedge\lnot r\wedge w)\\ \end{array}\end{split}\]

Propositions in DNF are just what we need to deal with input/output tables of the type that we have been discussing. Any such table can be computed by a proposition in disjunctive normal form. It follows that it is possible to build a circuit to compute that table using only and, or, and not gates.

Theorem 2.3

Consider a table that lists a logical output value for every combination of values of several propositional variables. Assume that at least one of the output values is true. Then there is a proposition containing those variables such that the value of the proposition for each possible combination of the values of the variables is precisely the value specified in the table. It is possible to choose the proposition to be in disjunctive normal form.

Proof. Consider any row in the table for which the output value is \(\mathbb{T}\). Form a conjunction of simple terms as follows: For each variable, \(p\), whose value is \(\mathbb{T}\) in that row, include \(p\) itself in the conjunction; for each variable, \(q\), whose value is \(\mathbb{F}\) in the row, include \(\lnot q\) in the conjunction. The value of this conjunction is \(\mathbb{T}\) for the combination of variable values given in that row of the table, since each of the terms in the conjuction is true for that combination of variables. Furthermore, for any other possible combination of variable values, the value of the conjunction will be \(\mathbb{F}\), since at least one of the simple terms in the conjunction will be false.

Take the disjunction of all such conjunctions constructed in this way, for each row in the table where the output value is true. This disjunction has the value \(\mathbb{T}\) if and only if one of the conjunctions that make it up has the value \(\mathbb{T}\)—and that is precisely when the output value specified by the table is \(\mathbb{T}\). So, this disjunction of conjunctions satisfies the requirements of the theorem.

□

Note

This is the first proof of a non-trivial claim that we’ve seen. You will learn about theorems and proofs, and proof techniques, at the end of this chapter and in Section 3.

As an example, consider the table in Table 2.3. This table specifies a desired output value for each possible combination of values for the propositional variables \(p\), \(q\), and \(r\). Look at the second row of the table, where the output value is true. According to the proof of the theorem, this row corresponds to the conjunction \((\lnot p\wedge\lnot q\wedge r)\). This conjunction is true when \(p\) is false, \(q\) is false, and \(r\) is true; in all other cases it is false, since in any other case at least one of the terms \(\lnot p\), \(\lnot q\), or \(r\) is false. The other two rows where the output is true give two more conjunctions. The three conjunctions are combined to produce the DNF proposition \((\lnot p\wedge\lnot q\wedge r) \vee (\lnot p\wedge q\wedge r) \vee (p\wedge q\wedge r)\). This proposition computes all the output values specified in the table. Using this proposition as a blueprint, we get a logic circuit whose outputs match those given in the table.

Table 2.3 An input/output table specifying a desired output for each combination of values of the propositional variables \(p\), \(q\), and \(r\). Each row where the output is \(\mathbb{T}\) corresponds to a conjunction, shown next to that row in the table. The disjunction of these conjunctions is a proposition whose output values are precisely those specified by the table.#

\(p\)

\(q\)

\(r\)

output

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\((\lnot p\wedge\lnot q\wedge r)\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\((\lnot p\wedge q\wedge r)\)

\(\mathbb{T}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\(\mathbb{F}\)

\(\mathbb{F}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\(\mathbb{T}\)

\(p\wedge q\wedge r\)

Now, given any combinatorial logic circuit, there are many other circuits that have the same input/output behaviour. When two circuits have the same input/output table, the compound propositions associated with the two circuits are logically equivalent. To put this another way, propositions that are logically equivalent produce circuits that have the same input/output behaviour. As a practical matter, we will usually prefer the circuit that is simpler. The correspondence between circuits and propositions allows us to apply Boolean algebra to the simplification of circuits.

Tip

Our preference for simpler applies to compound propositions, whether or not they correspond to circuits. We usually prefer the equivalent form of the proposition that is simpler. Any proposition has an equivalent proposition in DNF. So when proving a theorem about compound propositions, it is sufficient to consider only DNF propositions. This can make the proof easier to write.

For example, consider the DNF proposition corresponding to the table in Table 2.3. In \((\lnot p\wedge\lnot q\wedge r) \vee (\lnot p\wedge q\wedge r) \vee (p\wedge q\wedge r)\), we can factor \((q\wedge r)\) from the last two terms, giving \((\lnot p\wedge\lnot q\wedge r) \vee ((\lnot p\vee p) \wedge (q\wedge r))\). Since \(\lnot p\vee p\equiv\mathbb{T}\), and \(\mathbb{T}\wedge Q\equiv Q\) for any proposition \(Q\), this can be simplified to \((\lnot p\wedge\lnot q\wedge r) \vee (q\wedge r)\). Again, we can apply the distributive law to this to factor out an \(r\), giving \(((\lnot p\wedge \lnot q)\vee q)\wedge r)\). This compound proposition is logically equivalent to the one we started with, but implementing it in a circuit requires only five logic gates, instead of the ten required by the original proposition.[1]

If you start with a circuit instead of a proposition, it is often possible to find the associated proposition, simplify it using Boolean algebra, and use the simplified proposition to build an equivalent circuit that is simpler than the original. And simplifying a proposition to DNF is often a sensible approach.

Video

One way to simplify propositions is using a Karnaugh-map (or K-map for short) as you will learn in Computer Organisation. Using a K-map you can find what they will call a ‘minimal sum of products’. Notice that a sum of products is just a proposition written in DNF. For the course of Reasoning & Logic we may ask you to translate propositions to a DNF form. You can then choose to either do so using rewrite rules, but you are also free to use a K-map if you prefer. In one of the pencasts of this course we show how both methods lead to a result in DNF: youtu.be/GwVngCU9eYY.

2.3.5. Binary addition*#

All this explains nicely the relationship between logic and circuits, but it doesn’t explain why logic circuits should be used in computers in the first place. Part of the explanation is found in the fact that computers use binary numbers. A binary number is a string of zeros and ones. Binary numbers are easy to represent in an electronic device like a computer: Each position in the number corresponds to a wire. When the wire is on, it represents one; when the wire is off, it represents zero. When we are thinking in terms of logic, the same states of the wire represent true and false, but either representation is just an interpretation of the reality, which is a wire that is on or off. The question is whether the interpretation is fruitful.

Once wires are thought of as representing zeros and ones, we can build circuits to do computations with binary numbers. Which computations? Any that we want! If we know what the answer should be for each combination of inputs, then by Theorem 2.3 we can build a circuit to compute that answer. Of course, the procedure described in that theorem is only practical for small circuits, but small circuits can be used as building blocks to make all the calculating circuits in a computer.

Table 2.4 Input/output tables for the addition of three binary digits, \(A\), \(B\), and \(C\).#

\(A\)

\(B\)

\(C\)

output

0

0

0

0

0

0

1

1

0

1

0

1

0

1

1

0

1

0

0

1

1

0

1

0

1

1

0

0

1

1

1

1

\(A\)

\(B\)

\(C\)

output

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

1

For example, let’s look at binary addition. To add two ordinary, decimal numbers, you line them up one on top of the other, and add the digits in each column. In each column, there might also be a carry from the previous column. To add up a column, you only need to remember a small number of rules, such as \(7+6+1=14\) and \(3+5+0=8\). For binary addition, it’s even easier, since the only digits are 0 and 1. There are only eight rules:

\[\begin{split}\begin{align*} 0+0+0&=00 & 1+0+0&=01\\ 0+0+1&=01 & 1+0+1&=10\\ 0+1+0&=01 & 1+1+0&=10\\ 0+1+1&=10 & 1+1+1&=11\\ \end{align*}\end{split}\]

Here, we’ve written each sum using two digits. In a multi-column addition, one of these digits is carried over to the next column. Here, we have a calculation that has three inputs and two outputs. We can make an input/output table for each of the two outputs. The tables are shown in Table 2.4. We know that these tables can be implemented as combinatorial circuits, so we know that circuits can add binary numbers. To add multi-digit binary numbers, we just need one copy of the basic addition circuit for each column in the sum.

2.3.6. Exercises#