2. Fourier series

The Fourier series of a function expresses the function as a linear combination of complex exponentials. This is extremely useful in many situations in mathematics, physics and engineering.

In terms of linear algebra, the theory of Fourier series provides an orthonormal basis for the Hilbert space of square-integrable functions on the interval \([0,1]\); see also Hilbert spaces.

2.1. Definition and basic properties

Definition 2.1 (Fourier series)

Let \(f\) be a (real or complex) function on the interval \([0,1]\). The Fourier series of \(f\) is the infinite series

(2.1)\[ \sum_{n=-\infty}^\infty c_n \exp(2\pi i n x) \]

where the complex numbers \(c_n\) are defined by

\[ c_n = \int_0^1 f(x)\exp(-2\pi i n x)dx. \]

We call these \(c_n\) the Fourier coefficients of \(f\).

One reason why Fourier series are useful is that the basis functions

\[ e_n(x) = \exp(2\pi i n x) \]

form an orthonormal system: in Exercise 2.1, you will show that these functions satisfy

\[\begin{split} \int_0^1 e_m(x)\overline{e_n(x)}dx = \begin{cases} 1& \text{if }m=n,\\ 0& \text{if }m\ne n. \end{cases} \end{split}\]

(See also Example 8.7 in the section on Hilbert spaces.)

There are also other ways of writing this series, namely via Euler’s formula

(2.2)\[ \exp(i x)=\cos x + i\sin x \]

or the equivalent form

\[\begin{split} \begin{aligned} \cos x &= \frac{\exp(ix)+\exp(-ix)}{2},\\ \sin x &= \frac{\exp(ix)-\exp(-ix)}{2i}. \end{aligned} \end{split}\]

In particular, for functions \(f\) satisfying \(f(1-x)=f(x)\) this gives rise to Fourier cosine series

\[ f(x) = \sum_{n=0}^\infty a_n \cos(2\pi n x) \]

and for functions \(f\) satisfying \(f(1-x)=-f(x)\) to Fourier sine series

\[ f(x) = \sum_{n=1}^\infty b_n \sin(2\pi n x); \]

see Exercise 2.4 for details.

For most functions \(f\) that one encounters in practice, the Fourier series of \(f\) converges to \(f\) at every point. However, it is possible to come up with ‘pathological’ examples of functions (even continuous ones) where this fails. For an example where \(f\) is discontinuous, see Exercise 2.2.

Remark 2.1

In signal processing, one of the most fundamental uses of Fourier series is in decomposing a signal on a bounded interval (the unit interval \([0,1]\) in our case), or a periodic signal, as a sum of the signals \(\exp(2\pi i n x)\) with ‘pure’ frequency \(n\). In a slightly different direction, Fourier series are also closely related to the Z-transform (Wikipedia) used in signal processing. Suppose we start with an arbitrary sequence of complex numbers \(c_n\) for integers \(n\) (not necessarily coming from a function \(f\) on the unit interval). Such a sequence can be interpreted as a signal in discrete time. In the expression for the Fourier series (2.1), we can rewrite \(\exp(2\pi i n x)\) as \(z^n\), obtaining the series \(\sum_{n=-\infty}^\infty c_n z^n\). We can now take \(z\) (which lies on the complex unit circle if \(x\) is real) to vary over a suitable region within the complex plane where the series converges. This series can then be studied as a function of \(z\), known as the \(Z\)-transform of the signal.

2.2. Examples

2.2.1. The Fourier series of a sawtooth function

Consider the function \(f(x)=x\) on the interval \([0,1]\). To find its Fourier series, we compute the integrals defining the coefficients \(c_n\) for all integers \(n\). We have

\[ c_0 = \int_0^1 x dx = \frac{1}{2}. \]

For \(n\ne0\) we compute \(c_n\) using integration by parts:

\[\begin{split} \begin{aligned} c_n &= \int_0^1 x\exp(-2\pi i n x)dx\\ &= \left.-\frac{1}{2\pi i n}x\exp(-2\pi i n x)\right|_{x=0}^1 +\frac{1}{2\pi i n}\int_0^1\exp(-2\pi i n x)dx\\ &= \left(-\frac{1}{2\pi i n}+0\right)+0\\ &= -\frac{1}{2\pi i n}. \end{aligned} \end{split}\]

We conclude that the Fourier series of \(f\) is

\[ \frac{1}{2}-\sum_{n\ne0}\frac{1}{2\pi i n}\exp(2\pi i n x), \]

where the sum ranges over all non-zero integers \(n\). Combining the terms corresponding to \(n\) and \(-n\) and using the identity

\[ -\frac{1}{2\pi i n}\exp(2\pi i n x) + \frac{1}{2\pi i n}\exp(2\pi i (-n) x) = -\frac{1}{\pi n}\sin(2\pi n x), \]

we can simplify this to

\[ \frac{1}{2}-\sum_{n=1}^\infty\frac{1}{\pi n}\sin(2\pi n x), \]

Show code cell source

Hide code cell source

from _modules.series_utils import get_pointwise_values
from myst_nb import glue
import numpy as np
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import sympy as sp
from sympy.abc import x

f = x
series = sp.fourier_series(f, (x, 0, 1))
domain = np.arange(0, 1, 0.01)

# Create figure
fig = make_subplots(
    rows=2, cols=1,
    subplot_titles=("f(x) = x", "Fourier series approximation"),
    vertical_spacing=0.2,
)

fig.add_trace(
    go.Scatter(
        visible=True,  # Always visible
        line=dict(color="red", width=2),
        x=domain,
        y=domain,  # Since f(x) = x, the y values are the same as the domain
        showlegend=False,
        name="Sawtooth fn."
    ),
    row=1, col=1
)

# Add traces, one for each slider num_terms
for num_terms in np.arange(1, 21, 1):
    series_trunc = series.truncate(num_terms)
    
    fig.add_trace(
        go.Scatter(
            visible=False,
            line=dict(color="blue", width=2),
            x=domain,
            y=get_pointwise_values(series_trunc, domain),
            showlegend=False,
            name=f"{num_terms}-term appx."
        ),
        row=2, col=1
    )

# Make 10th trace visible
fig.data[10].visible = True

# Create and add slider
steps = []
# Mapping the first term with i = 1 rather than i = 0
# because it is a term (albeit a constant) and
# to keep it consistent with sympy's truncate function
for i in range(1, len(fig.data)):
    # Ensure that the first trace (f(x)=x) is always visible
    step = dict(
        method="update",
        args=[{"visible": [True] + [False] * (len(fig.data) - 1)}],
        label=(i)
    )
    step["args"][0]["visible"][0] = True  # Always keep f(x)=x visible
    step["args"][0]["visible"][i] = True  # Toggle i'th Fourier series trace to "visible"
    steps.append(step)

sliders = [dict(
    # Setting the 10-term approximation as default
    # using active=(10-1) because now indexing starts at 0
    # in the sliders list
    active=9, 
    currentvalue={"prefix": "Num. of terms: "},
    pad={"t": 50},
    steps=steps
)]

fig.update_layout(
    sliders=sliders,
    height=800,
    width=750
)

glue("sawtooth", fig)

Fig. 2.1 A sawtooth function and an approximation to its Fourier series

2.2.2. The Fourier series of a half-wave rectified sine function

Consider the half-wave rectified sine function

(2.3)\[\begin{split} f(x) = \begin{cases} \sin(2\pi x)& \text{if }0\le x\le 1/2,\\ 0& \text{if }1/2<x\le 1. \end{cases} \end{split}\]

In Exercise 2.3, you will show that the Fourier coefficients are given by

(2.4)\[\begin{split} \begin{aligned} c_1 &= \frac{1}{4i},\quad c_{-1}=-\frac{1}{4i},\\ c_n &= 0\text{ for $n\ne\pm1$ odd},\\ c_n &= -\frac{1}{\pi(n^2-1)}\quad\text{for $n$ even}. \end{aligned} \end{split}\]

Show code cell source

Hide code cell source

from matplotlib import pyplot as plot
from myst_nb import glue
from numpy import linspace, sin, cos, heaviside, pi

fig, ax = plot.subplots(2, 1, figsize=(8,8))

x = linspace(0, 1, 101)

ax[0].plot(x, sin(2*pi*x) * heaviside(0.5-x, 0.5), color='red')
ax[0].set_xlabel('$x$')
ax[0].set_ylabel('$f(x)$')

f_appr = 1/pi + 1/2*sin(2*pi*x) - 2/pi * sum((1/((2*n)**2-1)*cos(2*pi*(2*n)*x) for n in range(1, 3)), 0*x)
ax[1].plot(x, f_appr, color='blue')
ax[1].set_xlabel('$x$')
ax[1].set_ylabel('Fourier series of $f$ up to $n=4$')

glue("rectified-sine", fig)

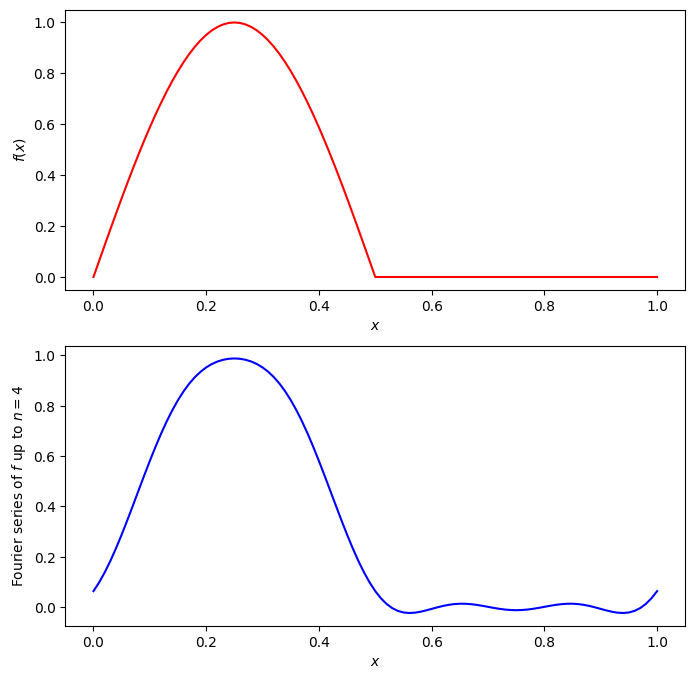
Fig. 2.2 A half-wave rectified sine function and an approximation to its Fourier series

---

In the applet below (simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu)) you can get a feeling for Fourier series by working with them interactively.

---

2.3. Exercises

Exercise 2.1

Prove the orthogonality relation

\[\begin{split} \int_0^1 e_m(x)\overline{e_n(x)}dx = \begin{cases} 1& \text{if }m=n,\\ 0& \text{if }m\ne n \end{cases} \end{split}\]

where

\[ e_n(x) = \exp(2\pi i n x). \]

Hint

You can integrate a complex exponential function in the same way as a real one. Alternatively, you can use Euler’s formula (2.2).

Exercise 2.2

Consider the function \(f\) on the interval \([0,1]\) defined by

\[\begin{split} f(x) = \begin{cases} 1& \text{if }0\le x\le 1/2,\\ 0& \text{if }1/2<x\le 1. \end{cases} \end{split}\]

1. Compute the Fourier series of \(f\).

2. Compute the value of this Fourier series at \(x=1/2\).

Exercise 2.3

Consider the the half-wave rectified sine function \(f\) defined by (2.3).

1. Prove the formula (2.4) for the Fourier coefficients of \(f\).

2. Show that the Fourier series of \(f\) can be rewritten as

   \[ f(x) = \frac{1}{\pi} + \frac{1}{2}\sin(2\pi x) - \frac{2}{\pi} \sum_{n>0\text{ even}} \frac{1}{n^2-1}\cos(2\pi nx). \]

Exercise 2.4

Consider a complex-valued function \(f\) on the interval \([0,1]\) with Fourier series

\[ f(x)=\sum_{n=-\infty}^\infty c_n\exp(2\pi i nx). \]

1. Show that \(f\) can be written as a Fourier cosine series if and only if \(f(1-x)=f(x)\).

2. Show that \(f\) can be written as a Fourier sine series if and only if \(f(1-x)=-f(x)\).